Can Your Team Self-Organize?

You and your colleagues must arrange yourselves in a specified numerical order, but without knowing each other’s numbers. How long of an increasing sequence will you generate?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. The “Extra Credit” is where the analysis typically gets hairy, or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

In a recent team building exercise at work, a group of people (including myself) was asked to quantify themselves in various ways. For example: “What outdoor temperature do you prefer?” No one reveals their answer at first. Instead, each person places a card with their name on an unmarked line, one at a time. In this example, folks who prefer higher temperatures would place their names farther right; folks who prefer lower temperatures would place their names farther left. However, the line is unmarked and doesn’t have any units.

Once all the names are placed on the line, their values are revealed. For example, a group of six might have generated the following numbers, in order from left to right on the line: 60, 67, 65, 74, 70, 80.

The team’s score is the length of the “longest increasing subsequence.” In other words, it’s the maximum number of elements in the list you can keep such that they form an increasing subsequence. In the example above, you can remove the 67 and the 74 to get the following increasing subsequence with four numbers: 60, 65, 70, 80. There are a few other ways to get an increasing subsequence of length four, but there’s no way to get a sequence of length five or more, so the team’s score is four.

Suppose a total of four people are participating in this team building exercise. They all write down different numbers, and then independently place their names at random positions on the line.

On average, what do you expect the team’s score to be?

This Week’s Extra Credit

Instead of four people, now suppose there are 10 people participating in the team building exercise. As before, they all write down different numbers, and then independently place their names at random positions on the line.

On average, what do you expect the team’s score to be?

Making the ⌊Rounds⌉

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing that I posed to ChatGPT-5 Thinking all 20 of the Q3 puzzles for which answers have been published. The AI had not seen any of these puzzles before, as their publication here came well after its knowledge cutoff.

As I expected, the AI did quite well, correctly answering 17 of the 20 questions on its very first attempt. After a few minutes of thought per puzzle, each answer came with a rather concise explanation, one of which is included below for last week’s Fiddler. You will see that ChatGPT-5 now appears in the standings, although it is not eligible for a t-shirt prize.

So, which three puzzles among the 20 did the AI get wrong? They were:

• The Extra Credit from July 4, which asked you to count the number of parallelograms whose vertices were stars on the American flag. The correct answer was 5918, whereas ChatGPT-5 offered an answer of 6200.

• The Fiddler from August 1, in which you had to squeeze squares together. ChatGPT-5 fell into the same “trap” as many readers, thinking the answer was 2 + 1/√2, rather than the correct answer of 3. Meanwhile, the AI did get the Extra Credit correct, which involved more computation but lacked a trap.

• The Extra Credit from August 15, in which you had to state how much money you had at least a 50 percent of winning using casino vouchers. The correct strategy was to go all-or-nothing on $55 at first. Then, the 50 percent of the time you won, you could guarantee yourself another $35. ChatGPT-5 knew both of these things, but still submitted a response of $55. With an additional prompt, it realized that these values had to be added. Nevertheless, I counted this as incorrect on the first attempt.

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Standings

I’m tracking submissions from paid subscribers and compiling a leaderboard, which I’ll reset every quarter. All correct solutions to Fiddlers and Extra Credits are worth 1 point each. Solutions should be sent prior to 11:59 p.m. the Monday after puzzles are released. At the end of each quarter, I’ll 👑 crown 👑 the finest of Fiddlers. If you think you see a mistake in the standings, kindly let me know.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Lowell Vaughn 🎻 from Bellevue, Washington. I received 50 timely submissions, of which 44 were correct—good for an 88 percent solve rate.

In the game of Letter Boxed from The New York Times, you must connect letters together around a square to spell out words. However, from any given letter, the next letter cannot be on the same side of the square.

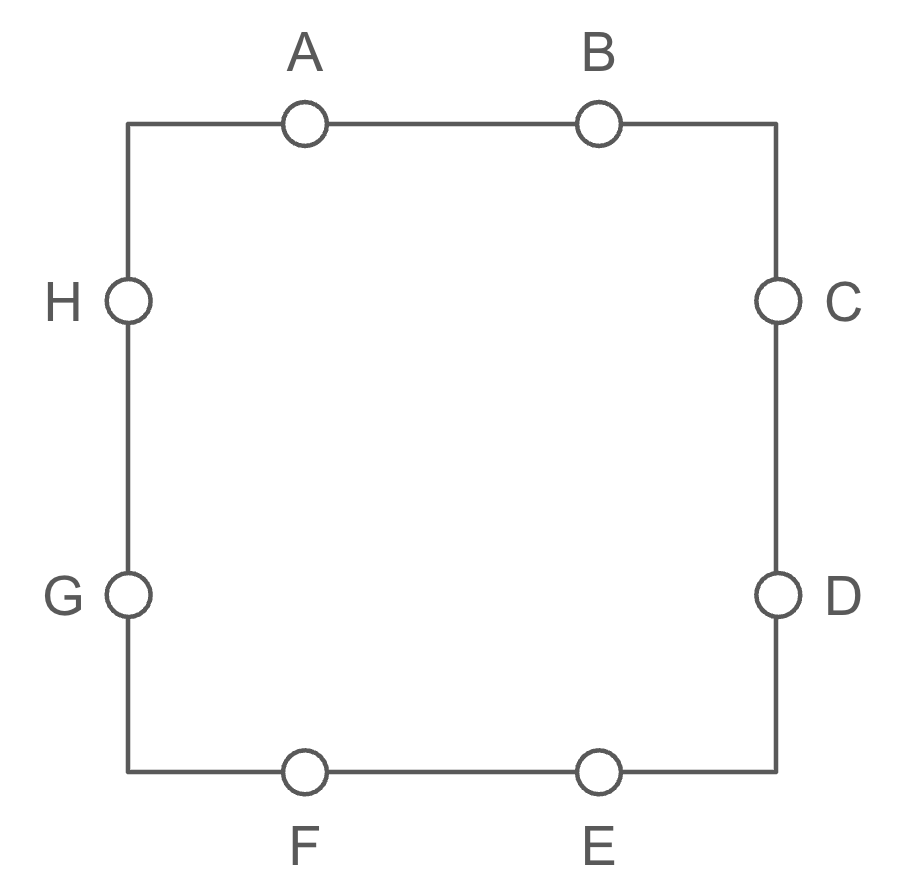
Last week, you considered the following diagram, which consisted of eight points (labeled A through H), two on each side of the square. A valid “letter boxed” sequence started at any of the eight points, and proceeded through all of the other points exactly once. However, adjacent points in the sequence could never be on the same side of the square. The first and last points in the sequence could be on the same side, but didn’t have to be.

As an illustration, AFBCHEDG was a valid sequence of points. However, AFBCHGED was not a valid sequence, since H and G were adjacent in the sequence and on the same side of the square.

How many distinct valid “letter boxed” sequences were there that included all eight points on the square?

There were 8!, or 40,320, ways to order eight letters without any constraints. However, many of these orderings (like AFBCHGED) were invalid, so the answer had to be less than 40,320. To determine the exact answer, solver Eric Bill counted up all the sequences, thinking carefully about how many were duplicates of each other if the sides or letters on a side were swapped around.

A sequence could have started from any of the eight points, so let’s pick point A. Then, at the end, we’ll multiply our number of sequences that start with A by eight to get the final answer. From there, you could have gone to any of the six points not on the first point’s side. Let’s pick C as our second point, and at the end we’ll multiply our paths that start with AC by 8·6, or 48.

From there, things got a little more complicated.

Suppose the next two points in the sequence were B and D. At this point, you have visited all the points A through D, and you still had to visit E through H. You could have visited any of those four points next, after which you had to visit one of the two points on the other side of the square; after that, the last two points were determined. So there were eight sequences that started with ACBD.

Suppose, instead, the next two points in the sequence (after A and C) were B and E. If the next point was D, then the point after that could not have been F. Why? Because that would have left G and H as the final two points, and you couldn’t travel between them. So after D, you had to visit G or H, then come back to F, and finally go to H or G (whichever one you didn’t visit earlier). Alternatively, you could have gone from E to G or H. After picking one of these two points, you still had to travel to three points on three different sides of the square, one of which was on the side you just visited. To knock out these last three points, you could pick from among two of them, then from among two of them again, and the last point was determined. Putting this all together, there were 10 sequences that started with ACBE.

The same went for ACBF, ACBG, and ACBH. Each resulted in 10 sequences, for a total of 48 sequences that started with ACB.

Phew! Now, what if the third point selected had been E? If the fourth point was B or D, you’ve now visited four points, two of which were on the same side. From there, you had 12 ways to complete the path (see if you can work them out!). Together, ACEB and ACED accounted for 24 total sequences.

Finally, if the third point was E, the fourth point could have been on the fourth side of the square. There were two such points (G and H), after which you had knocked out one point on each side of the square. From there, you had three points to choose from, then another three, then two, and then the final point was determined. Together, ACEG and ACEH accounted for 36 sequences.

All told, we had 60 sequences that started with ACE. The same went for ACF, ACG, and ACH—all the cases in which the first three points were on three distinct sides. Combining these, there were 4·60 = 240 sequences. Along with the 48 sequences we previously found that started with ACB, there were 288 that started with AC.

Our plan was to find all the paths that started with AC, which we have now done, and multiply that by 48. Thus, the final answer was 48·288 = 13,824.

Excellent! Now, how did ChatGPT-5 solve this problem?

Let the four sides be pairs {A,B}, {C,D}, {E,F}, {G,H}. A valid sequence is a permutation of A–H with no adjacent letters from the same pair.

Let E_i be the event that the i-th pair appears adjacent (in either order). For any chosen set of k pairs to be adjacent, treat each as a block: there are 2^k ways to order the letters inside the k blocks and (8 − k)! ways to arrange the resulting 8 − k items.

By inclusion–exclusion, N = Σ_{k=0}^4 (−1)^k C(4,k) 2^k (8 − k)! = 8! − 4·2·7! + 6·4·6! − 4·8·5! + 1·16·4! = 40320 − 40320 + 17280 − 3840 + 384 = 13824.

To put it less concisely, ChatGPT started by counting up all the possible sequences, which was 8!, and subtracting off all the sequences with one adjacent pair among {A,B}, {C,D}, {E,F}, and {G,H}. However, sequences with two such adjacent pairs were double counted, and had to be added back in. But then sequences with three adjacent pairs were double counted the other way, and had to be removed again. Finally, sequences with four adjacent pairs were double counted, and had to be added back in. This process of iteratively double-counting and correcting in either direction is the “inclusion-exclusion principle” that ChatGPT was referring to. (Kudos to solver solvers like Jonathan Schwartz and Michael Schubmehl, who also used inclusion-exclusion!)

So, yeah, it appears that ChatGPT knows what it’s doing.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Peter Exterkate 🎻 from Sydney, Australia. I received 33 timely submissions, of which 32 were correct, good for a 97 percent solve rate.

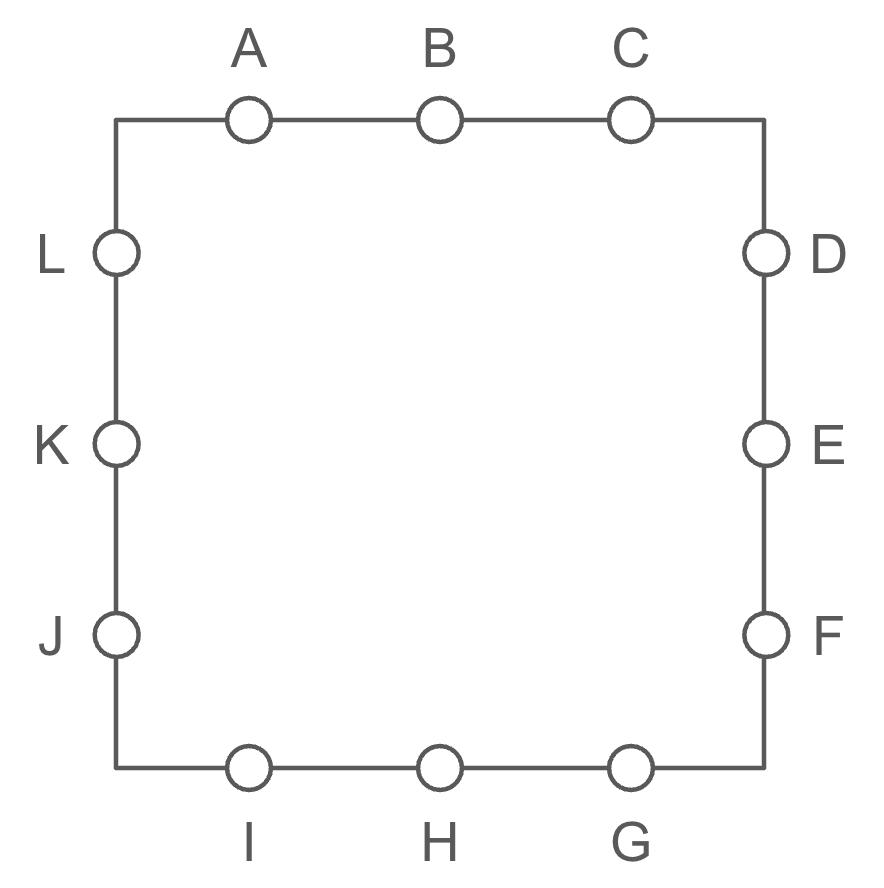
Instead of two points on each side of the square (and eight points in total), now there were three (and twelve points in total), labeled A through L in the diagram below.

How many distinct valid “letter boxed” sequences were there that include all 12 points on the square?