Can You Squeeze the Squares?

Place a unit square in a larger square region. If you do this cleverly, how large a region can you have such that you can’t add any more unit squares? What if you initially place three unit squares?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. The “Extra Credit” is where the analysis typically gets hairy, or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

There’s a square board with side length A. Your friend cleverly places a unit square on the board and challenges you to place another unit square on the board—without moving the first one—so that it too is entirely on the board and the squares don’t overlap. (The unit squares can touch each other.)

Alas, it’s impossible for you to do so! But there’s some minimum value of A for which you can always place a second unit square on the board, no matter how cleverly your friend places the first one.

What is this minimum value of A?

This Week’s Extra Credit

Now there’s another square board with side length B. This time, your friend cleverly places three unit squares (which can touch but not overlap) and issues a similar challenge, asking you to place one more unit square on the board.

Once again, it’s impossible for you to do so! But there’s some minimum value of B for which you can always place a fourth unit square on the board, no matter how cleverly your friend places the first three squares.

What is this minimum value of B?

Making the ⌊Rounds⌉

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a mathematical result from way back in December 2024, for which I’m clearly late to the party.

In 1807, it was proven that two polygons of equal area can always be cut into a finite number of pieces and rearranged to form each other. In 1903, Henry Dudeney was able to turn an equilateral triangle into a square of equal area (and vice versa) using only four pieces. On the off chance you’ve never seen this before, see if you can work it out for yourself!

So then what happened in December 2024? That’s when mathematicians (including my algorithms professor from college) proved that four pieces was indeed the fewest with which you could do this.

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Standings

I’m tracking submissions from paid subscribers and compiling a leaderboard, which I’ll reset every quarter. All correct solutions to Fiddlers and Extra Credits are worth 1 point each. Solutions should be sent prior to 11:59 p.m. the Monday after puzzles are released. At the end of each quarter, I’ll 👑 crown 👑 the finest of Fiddlers. If you think you see a mistake in the standings, kindly let me know.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Lise Andreasen 🎻 from Valby, Copenhagen, Denmark. I received 51 timely submissions, of which 46 were correct—good for a 90 percent solve rate.

Last week, you and a competitor were approaching the finish of a grueling stage of the Tour de Fiddler. One of you would win the stage, the other would come in second. As you approached the finish, each of you were going to test the feeling of your legs, which would be somewhere between 0 percent (“I can barely go on!”) and 100 percent (“I can do this all day!”). For the purposes of this puzzle, these values were chosen randomly, uniformly, and independently.

Immediately after feeling your legs, you and your opponent would each have a decision to make. Would you maintain your current pace, or would you sprint to the finish? Among those who sprinted for the finish, whoever’s legs were feeling the best would win the stage. But if no one sprinted for the finish, everyone had an equal chance of winning the stage. In the Tour de Fiddler, you each had to decide independently whether to sprint for the finish based on your legs—you didn’t have time to react to your opponent’s decision.

Normally, teams at the Tour de Fiddler keep their strategy close to the vest. But your opponent’s manager declared on international television that if your opponent’s legs were feeling 50 percent or better, they’d sprint for the finish.

As you were about to test your legs for the final sprint and see how they felt, what were your chances of winning the stage, assuming an optimal strategy?

First off, several readers asked what would happen if only one person (you or your opponent) sprinted. As the puzzle stated, “Among those who sprinted for the finish, whoever’s legs were feeling the best would win the stage.” If only one person sprinted, that person had to have the strongest legs among all sprinters (all one of them). So if only one person sprinted, that person was guaranteed the win.

Next, what did it mean to assume an “optimal strategy”? What even was a strategy in this problem? The only lever you had was deciding whether to sprint based on how your legs felt. In theory, the better your legs felt, the more likely it was that you should have sprinted. So a strategy could be defined by a single parameter L: if your legs felt better than L percent, you sprinted; otherwise, you didn’t.

To some readers, it was obvious that you should always sprint. No matter how terrible your legs were, you’d still win at least half the time (when your opponent didn’t sprint). That’s some great intuition, but let’s still rigorously work through the problem here.

A good place to start was to look at the edge cases, special values of L that didn’t require intense analysis. For example, suppose L was 50 percent. In this case, you and your opponent were operating with the exact same strategy. Neither of you was more likely to win than the other, and so your chances of winning were 50 percent.

What if L was 100 percent, meaning you’d only sprint if your legs felt perfect? Based on the setup in the problem, this occurred with probability zero, meaning you never actually sprinted. The 50 percent of the time your opponent sprinted, they won and you lost. Among the remaining 50 percent of the time, you won half the time. Overall, your chances of winning were just 25 percent. Yikes! You were better off when L was 50 percent.

And what if L was 0 percent, meaning you always sprinted? The 50 percent of the time your opponent didn’t sprint, you won and they lost. Now let’s look at the 50 percent of the time your opponent did sprint. Half the time your legs were less than 50 percent, so you lost the sprint. The other half the time, your legs were between 50 and 100 percent, just like your opponent, so that you each had a 50 percent chance of winning. In summary, half the time you won as the only sprinter, and an eighth of the time you won in a competitive sprint. Overall, your chances of winning were 5/8, or 62.5 percent. That was the best result so far!

But to definitively say that was the best possible result, you had to examine all possible strategies, meaning all values of L between 0 and 100 percent. You could do this using a 2-D area diagram, where the horizontal axis represented how your legs felt and the vertical axis represented how your opponent’s legs felt. (As noted by several readers, this was very similar to the analysis from the previous week’s puzzle about meeting up at the mall!)

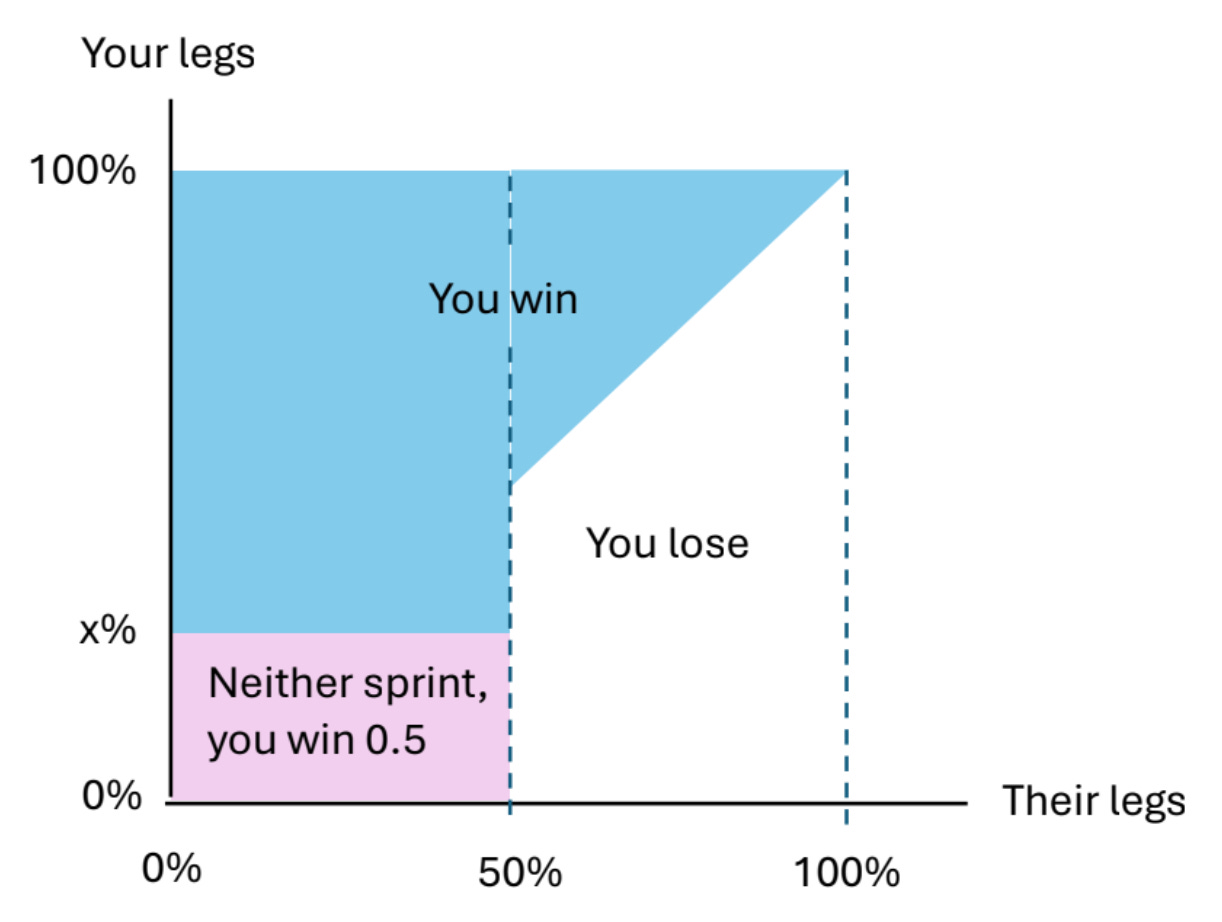
When L was between 0 and 50 percent, the diagram below, courtesy of solver Tom Singer (who labeled the variable “x” instead of “L”), showed the regimes in which you won, lost, or evenly split the chances with your opponent.

In this diagram, your probability of winning was the sum of the following cases:

• (1/2)·(1/2)·L, when neither of you sprinted

• (1/2)·(1−L), when you sprinted but your opponent did not

• (1/2)·(1/2)², when you both sprinted

The sum of these was 5/8−L/4.

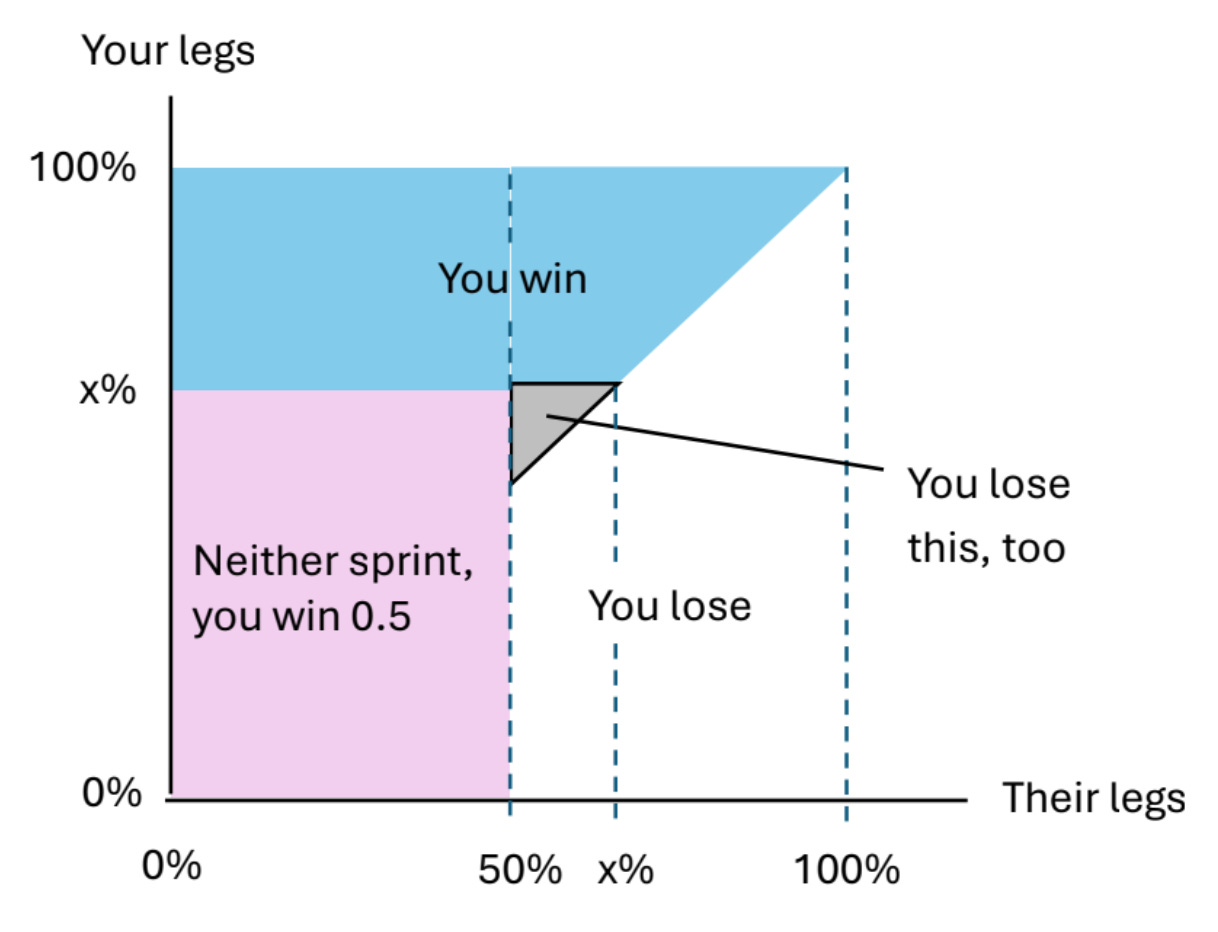
And when L was between 50 and 100 percent, it was this next diagram that showed the regimes:

In this second diagram, your probability of winning was the sum of the following cases:

• (1/2)·(1/2)·L, when neither of you sprinted

• (1/2)·(1−L), when you sprinted but your opponent did not

• (1/2)·(1/2)²−(1/2)·(L−1/2)², when you both sprinted

The key difference between this second diagram and the first one was the gray triangular regime, where you had better legs than your opponent but didn’t sprint. Anyway, the sum of these expressions was 1/2+L/4−L²/2.

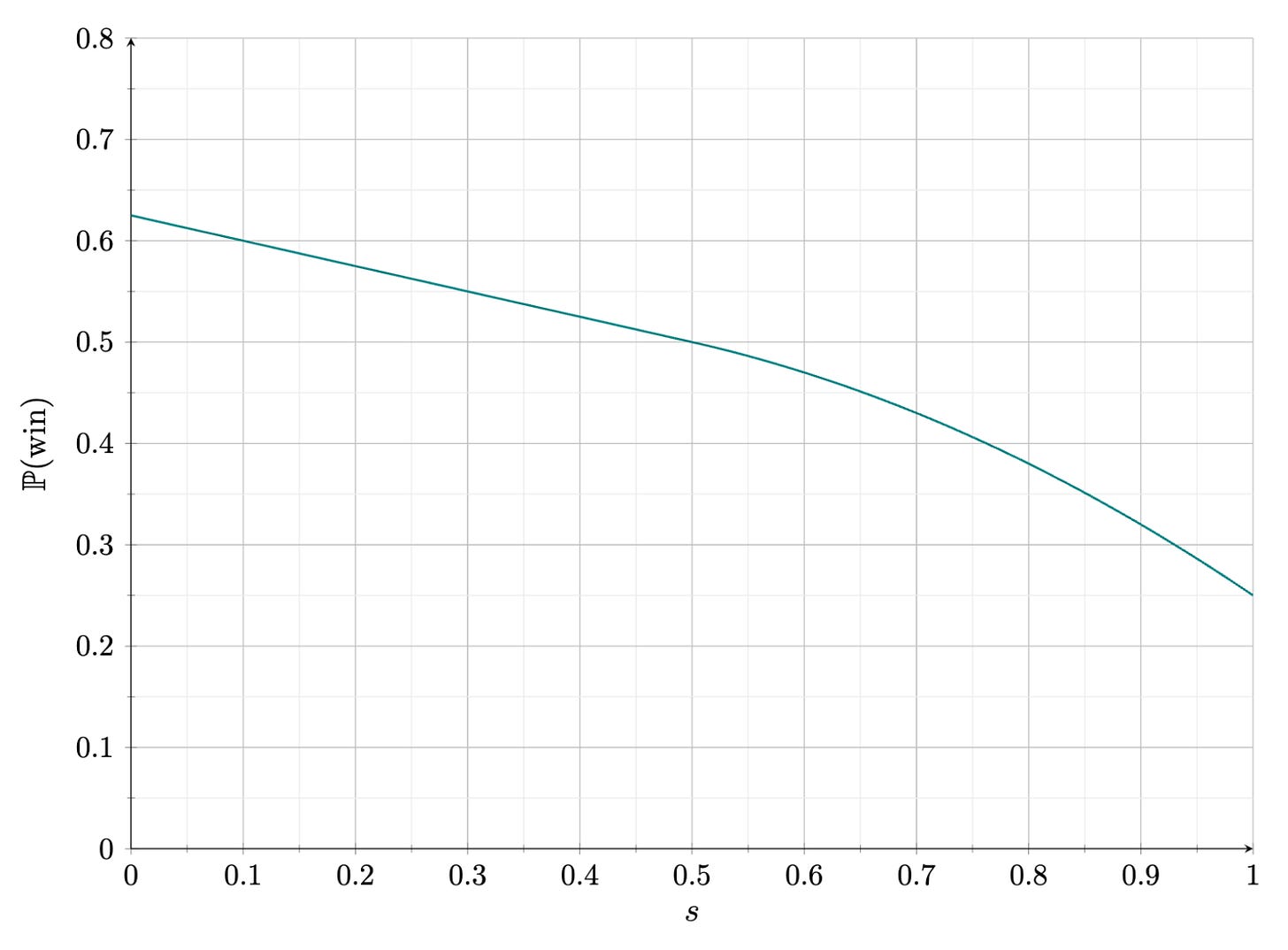
Putting these diagrams together, the graph below, courtesy of solver Cameron Jeffery (who labeled the variable “s” instead of “L”), showed your chances of winning as a function of L. It was encouraging to see the graph confirm the three edge cases (L = 0, 50, and 100 percent). Moreover, it confirmed that the optimal strategy was to always sprint (i.e., to set L = 0). That meant your chances of winning were indeed 5/8, or 62.5 percent.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Seth Cohen 🎻 from Concord, New Hampshire. I received 37 timely submissions, of which 28 were correct—good for a 76 percent solve rate.

Instead of one opponent, now you had two—meaning there were three riders in total. As luck would have it, the managers for both other riders proclaimed that they’d sprint for the finish as long as their legs were feeling 50 percent or better. Note that your opponents’ feelings were independent of each other.

As the three of you neared the finish, your own team manager radioed you the following message: “If your legs feel <garbled> percent or better, sprint for the finish!”

You couldn’t make out what the garbled part of the message was, and you were too tired to radio back for confirmation. Instead, you somehow mustered the energy to randomly, uniformly pick a number between 0 and 100 to fill in the blank from your manager’s message, thereby determining your racing strategy—optimization be damned!

Right before you chose your random strategy and tested your legs, what were your chances of winning the stage against both opponents?