Round, Round, Get a Round, I Get a Round

Pick some random numbers. Round them all and then add them up. Or add them all and then round the sum. How often do you get the same result, either way?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

Note: Due to the upcoming holiday, the next edition of Fiddler on the Proof will be coming out on September 6, 2024.

This Week’s Fiddler

Suppose you have two real numbers, like 3.14 and 2.718. If you round these two numbers and add these rounded values together, you get 3 + 3, or 6. Alternatively, if you add the original two numbers and then round the sum, you still get 6.

But rounding then adding doesn’t always give you the same result as adding then rounding. For example, if the two numbers are 2.4 and 3.4, rounding then adding gives you 5 (i.e., 2 + 3), whereas adding then rounding gives you 6 (i.e., 2.4 + 3.4 = 5.8, which rounds to 6).

How likely is it that rounding then adding gives you the same result as adding then rounding?

To be more precise, suppose you randomly, uniformly, and independently pick two real numbers between 0 and 1. What is the probability that rounding the two numbers and then adding gives you the same result as adding the two numbers and then rounding?

This Week’s Extra Credit

Instead of picking two numbers from the interval between 0 and 1, suppose you randomly and independently pick N numbers.

What is the probability that rounding each of the N numbers and then adding gives you the same result as rounding the sum of the N numbers?

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m a little embarrassed to share something I saw on one of those social media accounts that asks me to “shiver with ecstasy” at mathematical facts. But it did lead me to this fact, which is admittedly pretty neat, and which I’ll pose as a question here, spoiler-free:

Evaluate the following sum:

\(\frac{1}{e^{\pi}+1}+\frac{3}{e^{3\pi}+1}+\frac{5}{e^{5\pi}+1}+\ldots\)

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Chris Payne 🎻 from Arlington, Virginia. I received 44 timely submissions, of which 24 were correct—good for a (relatively meager) 55 percent solve rate.

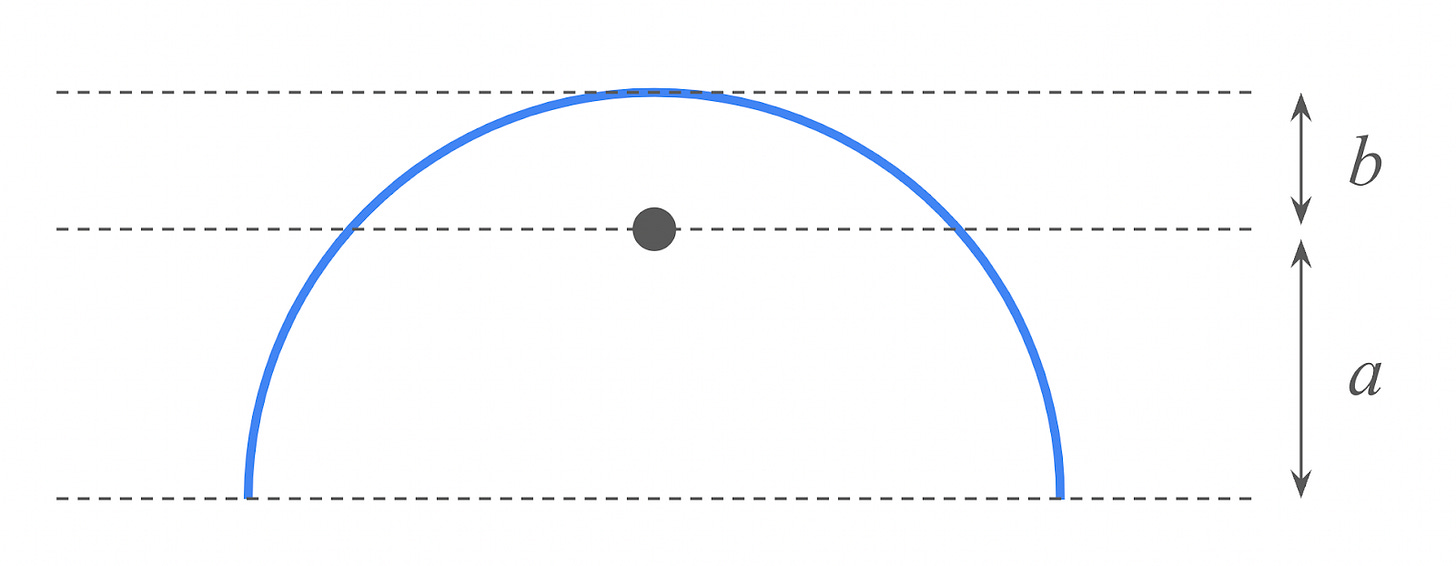
Last week, you looked at the high jump, an Olympic event in which an athlete’s entire body had to arc over a bar. We modeled the athlete mid-jump as a semicircle, centered over the bar, as shown in the diagram below. For simplicity, you assumed that their mass was uniformly distributed across the length of their body. The dot in the diagram represented the athlete’s center of mass.

The variable a represented the vertical distance between the athlete’s center of mass and their lowest points (presumably their outstretched fingers and toes), while b represented the vertical distance between the athlete’s center of mass and their highest point (presumably their waist).

What was the ratio a/b?

Many readers reasoned that the center of mass would be the point where half the athlete’s body was above it and half the athlete’s body was below it. If this were true, then the center of mass would have been the midpoint of a chord that was flanked by 45-degree arcs on either side, as illustrated below.

Assuming the semicircle had a radius R, the value of a would have been R·sin(45°), or R/√2. Meanwhile, the value of b would have been R·(1−cos(45°)), or R·(1−1/√2). Therefore, the ratio of a/b would have been (1/√2)/(1−1/√2), or 1/(√2−1). This could be further simplified to 1+√2, or approximately 2.414.

A total of 25 percent of readers submitted this answer. But it wasn’t correct!

Why? Because when calculating the center of mass, distance matters. If the athlete lifted their legs a little higher, just off the semicircle, then according to the above calculation, their center of mass wouldn’t have changed (i.e., half of them would still be above the point we found, and half of them would be below). But that’s nonsense! Of course if part of their body moves up, their center of mass moves up as well.

In statistical terms, the preceding calculation was analogous to finding the median of a distribution (50 percent is on either side), whereas center of mass is about finding the mean (the fulcrum around which both sides balance).

So instead of finding a point where half the athlete was above and half the athlete was below, we wanted to find that balancing point, where the sum of the distances from the center of mass to all the points above it equaled the sum of the distances to all the points below it. Put another way, the center of mass was the average vertical position of all the points on the semicircle.

Because you were dealing with a continuous curve, calculus was your friend when it came to computing that average vertical position. A few simplifying assumptions that didn’t affect the final answer:

• The circle was centered at the origin: (0, 0).

• The circle had radius 1.

• The linear density of the circle was 1.

Under these assumptions, the vertical position of the points on the semicircle were sin(𝜃) from 0 ≤ 𝜃 ≤ 𝜋. (Note that I switched from degrees to radians due to the imminent calculus.) The average height was therefore:

\(\frac{1}{\pi}\int_{0}^{\pi}\sin{\theta}d\theta\)

This integral evaluated to 2/𝜋, and was the value of a. Because we made the simplifying assumption this was a unit circle, b was equal to 1−a, or 1−2/𝜋. That meant the ratio a/b was 2/𝜋/(1−2/𝜋), or 2/(𝝅−2), which was approximately 1.752.

Because the athlete’s outstretched arms and legs were oriented vertically while their torso was mostly horizontal, their center of mass was lower than their median height, which meant the correct ratio (1.752) was less than what the prior, errant calculation gave (2.414).

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Mike Seifert 🎻 from New London, Connecticut. I received 35 timely submissions, of which 26 were correct—good for a 74 percent solve rate.

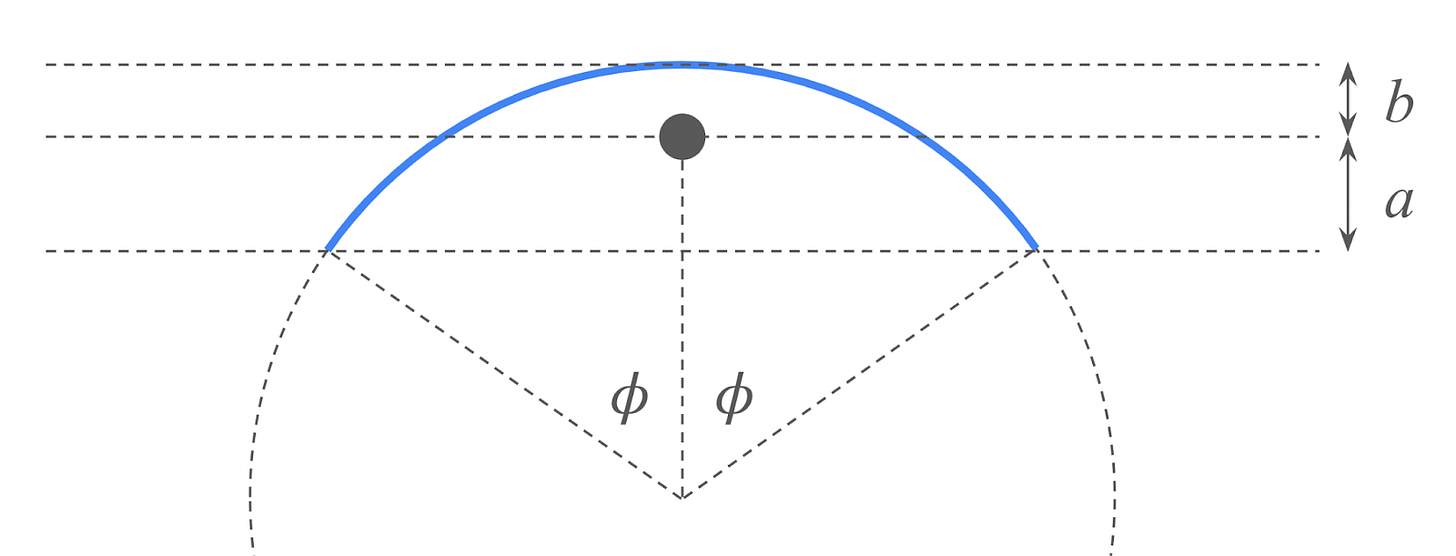
Instead of a semicircle, the athlete’s jump was now represented by an arc of angle 2𝜙 that was centered over the bar, as shown below:

As before, a represented the vertical distance between the athlete’s center of mass and their lowest points, while b represented the vertical distance between the athlete’s center of mass and their highest point.

As the angle 𝜙 got very, very small (i.e., in the limit as 𝜙 went to zero), what value did the ratio a/b approach?