How High Can You Jump?

A high jumper contorts into a circular arc with uniform density. Where’s their center of mass, and how far is it from their lowest and highest points?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

The puzzles from the last two weeks have both been about scoring at the Olympics, first in figure skating and then in gymnastics. This week’s puzzle isn’t about scoring, but rather about an event itself.

In the high jump, an athlete’s entire body must clear the bar. However, not every part of their body has to clear the bar at the same time. As a result, athletes arc their bodies over the bar, so that only a fraction of their mass is above the bar at any given time. In fact, athletes can theoretically clear the bar despite their center of mass remaining below the bar throughout the jump.

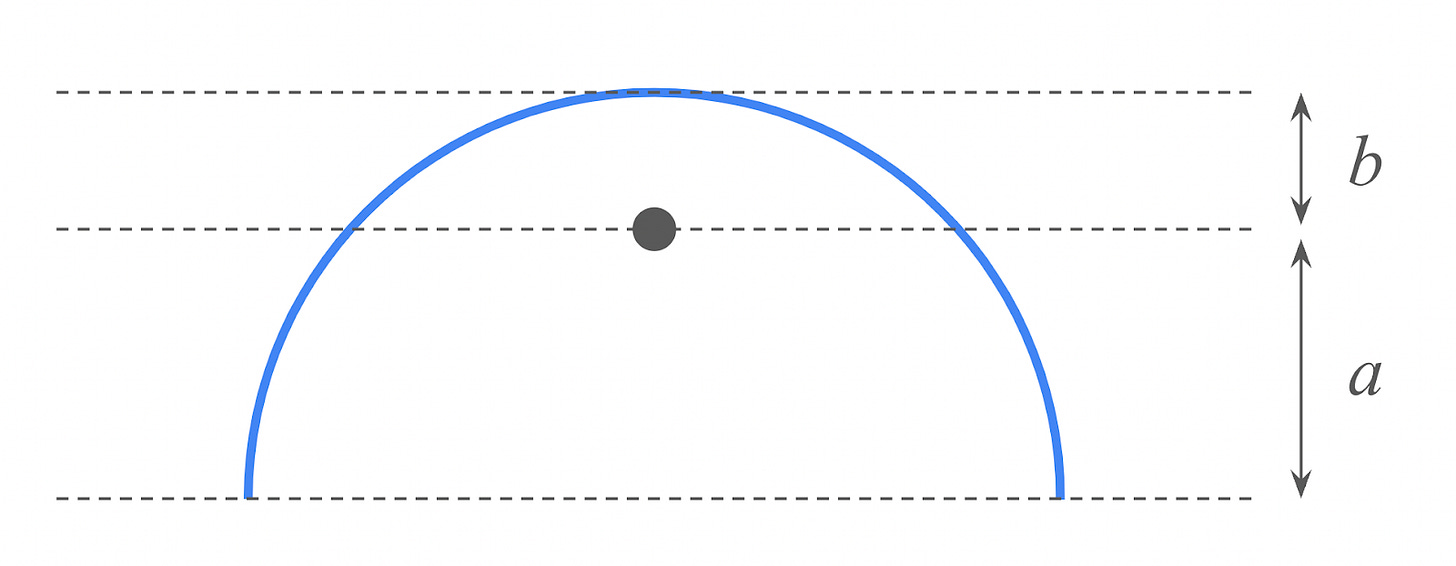
Let’s model the athlete mid-jump as a semicircle, centered over the bar, as shown in the diagram below. For simplicity, assume that their mass is uniformly distributed across the length of their body. The dot in the diagram represents the athlete’s center of mass.

Let a represent the vertical distance between the athlete’s center of mass and their lowest points (presumably their outstretched fingers and toes), and let b represent the vertical distance between the athlete’s center of mass and their highest point (presumably their waist).

What is the ratio a/b?

This Week’s Extra Credit

Instead of a semicircle, suppose the athlete’s jump is represented by an arc of angle 2𝜙 that is centered over the bar, as shown below:

As before, a represents the vertical distance between the athlete’s center of mass and their lowest points, while b represents the vertical distance between the athlete’s center of mass and their highest point.

As the angle 𝜙 gets very, very small (i.e., in the limit as 𝜙 goes to zero), what value does the ratio a/b approach?

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing an interesting question about Pythagorean triples that caught my attention by way of a post  from Benjamin Dickman.

I’ll paraphrase the question here, spoiler-free:

A primitive Pythagorean triple (a, b, c) is one in which a, b, and c are relatively prime (i.e., their greatest common divisor is 1).

If we write the ordered triple (a, b, c) in increasing order (i.e., with a < b < c), are there any integers that occur in all three spots at least once?

For example, 13 appears in the third slot for the primitive triple (5, 12, 13) and the first slot for the primitive triple (13, 84, 85). But 13 never appears in the second slot of any primitive triple.

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Dave Polidori 🎻 from Rancho Santa Fe, California. I received 42 timely submissions, of which 34 were correct—good for an 81 percent solve rate.

Last week, you investigated how scoring works in artistic gymnastics, in which competitors earn two subscores: one for difficulty and one for execution.

What’s weird (to me at least) is that the total score is calculated as difficulty plus execution, rather than difficulty times execution. If it were the latter, then the total score would scale linearly with both difficulty and execution. But apparently that’s not the case. So, how often do adding and multiplying subscores agree? That is, how often do they result in the same relative ranking?

To explore this, you supposed gymnast A had a difficulty score of 6.0, while gymnast B had a difficulty score of 5.0. If both gymnasts received independent, random execution scores between 0 and 10, what was the probability that their relative ranking would be the same, regardless of whether the subscores were added or multiplied? (Here, you were asked to assume the execution scores were real numbers that could go to any number of decimal places.)

There were two variables in this puzzle: A’s execution score (which we’ll call a) and B’s execution score (which we’ll call b). Algebraically, we could express A’s total score as 6+a (if subscores were added) or 6a (if subscores were multiplied). Similarly, we could express B’s total score as 5+b or 5b.

Instead of finding the probability the two scoring systems (adding and multiplying) agreed, let’s find the probability they disagreed, and then subtract that from 1 to find the probability of agreement. For the scoring systems to disagree, one of the following had to be true: addition favored B while multiplication favored A, or addition favored A while multiplication favored B. As inequalities, these two cases could be written as:

• 5+b > 6+a and 5b < 6a

• 5+b < 6+a and 5b > 6a

Since a and b were random real numbers, we didn’t have to worry about cases where the expressions on either side were precisely equal, as these were probability zero events.

To reduce the clutter, we could solve each of the inequalities for b:

• b > a+1 and b < 6/5·a

• b < a+1 and b > 6/5·a

In essence, we wanted to find the regions of the a/b coordinate plane that were between the lines b = a+1 and b = 6/5·a. (Also, these regions had to be inside the square defined by 0 ≤ a ≤ 10 and 0 ≤ b ≤ 10.)

Let’s look at these regions geometrically! The following graph shows the region above the line b = a+1 in red, and the region above b = 6/5·a in blue. The regions overlapped (purple) where B did better according to both scoring systems. Meanwhile, the unshaded (white) part shows where A did better according to both scoring systems. The systems disagreed in the blue and red regions, which were triangles that shared a common vertex at the point (5, 6).

The probability the systems disagreed was the combined area of these triangles divided by the total area of 10-by-10 square (which was 100).

What were the areas of the two triangles? The blue triangle had a base of 1 and a height of 5, so its area was 5/2. Meanwhile, the red triangle had a base of 2/3 (i.e., 9 − 25/3) and a height of 4, so its area was 4/3. Together, the triangles had a combined area of 23/6.

Dividing this by 100 told you the probability the scoring systems disagreed, which came to 23/600. The probability they agreed was 1 minus that value, or 577/600, roughly 96.2 percent. (If you submitted an answer of 23/600 and forgot to subtract from 1 at the end, I still gave you full credit.)

Based on this result, it might have seemed that the two scoring systems often agreed. Of course, that was over the whole range of possible execution scores for both gymnasts. When they had similar execution scores, the probability of agreement dropped significantly. And as I mentioned last week, the systems notably disagreed about the gold and silver medal in the women’s floor exercise.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 David P Combs 🎻 from Palm Springs, California. I received 30 timely submissions, of which 28 were correct—good for a 93 percent solve rate.

In addition to their execution scores, now you were asked to assume that both gymnasts’ difficulty scores were also independent, random values between 0 and 10.

What was the probability that their relative rankings would be the same, regardless of whether the subscores were added or multiplied? (Again, all subscores were real numbers that could go to any number of decimal places.)