Iceberg, Right Ahead!

They say 90 percent of an iceberg is hidden below the surface. But does that mean 90 percent of its length is hidden?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

Consider a large iceberg that’s a perfect cube. Thanks to the difference in densities between ice and water, 10 percent of the iceberg’s mass is above sea level, while the remaining 90 percent of the mass is below.

In its “optimal” orientation, the iceberg’s center of mass is as deep in the water as possible. Suppose the highest point (or points) of the iceberg is a distance x above sea level, while the lowest point (or points) of the iceberg is a distance y below sea level. What is the ratio of x to y?

Extra Credit

Instead of a cube, now suppose the iceberg is a perfect sphere. As before, suppose the highest point of the iceberg is a distance x above sea level, while the lowest point of the iceberg is a distance y below sea level.

What is the ratio of x to y?

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a video puzzle that’s a cute little nugget that many folks may have already seen in one form or another. Here’s a screenshot from the video:

In words: You have a “string of beads,” i.e., 25 circles of radius r are each tangent to their two neighbors. Their centers are all connected by radii that pass through the points of tangency. The portions of the circle that are “interior” to these radii are shaded blue. The portions exterior to the radii are shaded orange. What’s the difference between the orange area and the blue area, in terms of r?

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Emilie Mitchell 🎻 from Nashville, Tennessee. I received 43 timely submissions, of which 29 were correct—good for a modest solve rate of 67 percent.

Last week, the Fiddlerian government was in crisis! The Elephant Party, which possessed a majority of seats in the House, couldn’t seem to select a new Speaker. There were three candidates who wanted the job.

Here was their new plan to select a Speaker: All 221 members of the Elephant Party got in a room and voted for one of the three candidates. Each voter picked randomly from among the candidates—even if they themselves were one of the candidates!

If one candidate earned the majority of the votes, they became the next Speaker! Otherwise, the candidate with the fewest votes was eliminated and they repeated the process with one less candidate. If two or more candidates received the same smallest number of votes, then exactly one of them was eliminated at random.

They might have gotten lucky and selected their speaker in the first round of voting. After a second round, if it occurred, they would definitely have had a Speaker. That meant the average number of rounds needed was somewhere between one and two. What was this average?

Let’s face it. The odds of 221 members choosing randomly among three candidates and having a majority (i.e., at least 111 of them) pick the same candidate were pretty slim. That meant the average was almost 2 rounds—but not quite 2.

To work out the exact answer, my friends known as the “MassMutual Fiddler Crew” first found the probability that one of the candidates (let’s call them “A,” while the others were “B” and “C”) won a majority. According to the binomial distribution, the probability that A won k of the 221 votes was 221 choose k times (1/3)^k·(2/3)^221−k. From there, A won the majority for any value of k from 111 to 221. Adding up these 111 distinct cases meant the probability of A winning a majority was approximately 1.63×10^-7.

By symmetry, the remaining two candidates (B and C) had the same probability of winning the majority. And since only one candidate could ever win the majority at a time, you didn’t have to worry about double counting. So their collective chances of winning a majority were 4.89×10^-7. This was the probability of needing one round, whereas one minus this was the probability of needing two rounds. Setting p equal to 4.89×10^-7, the expected number of rounds was p+2·(1−p), which simplified to 2−p. As expected, this value was almost, but not quite, 2. It was approximately 1.99999951. (To get full credit, you had to submit an expression that was correct to seven decimal places. “Dang near two” was insufficient.)

I’m giving a special shoutout to solver Dan Dima of Bucharest, Romania, who submitted an exact fractional expression for this value:

617425657801704090874241098447827545759855219603833363268132854148075211286698861571172998889441418957637/308712904366595890319978599341504655567257431166409329421135089732346509723631627417356013073234099809467

Anyway, on average, the Elephant Party could expect 1.99999951 rounds of voting—and no shortage of continued chaos.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 David Kravitz  🎻 from Culver City, California. (Oh, Culver City.) I received 31 timely submissions, of which 23 were correct—good for a 74 percent solve rate.

For Extra Credit, you had to consider a contest with 10 (rather than three) candidates running for speaker. On average, how many rounds were needed until one candidate secured a majority of the 221 votes?

Among 10 candidates, the probability that A won k votes was now 221 choose k times (1/10)^k·(9/10)^221−k. Again, adding this up from k = 111 to k = 221 gave the probability of A winning in that first round. I’m not going to lie—things were not looking good for A in that first round. Their probability of securing a majority was roughly 1.87×10^-51. That’s equivalent to winning the Powerball jackpot … six times in a row. The probability of anyone securing a majority was just 10 times greater, or 1.87×10^-50.

One minus this probability gave you the chances of advancing to the second round, at which point you could again use the binomial distribution to compute the probability of declaring a winner versus going to the third round.

In the end, solvers like Chris Connett were able to compute the expected number of rounds by multiplying the probabilities of terminating after a given number of rounds by that corresponding number of rounds, and then summing those products. But that wasn’t really necessary, since the probabilities became vanishingly small with each additional candidate, the first seven rounds were effectively irrelevant. By the eighth round you had three candidates, and in the ninth you had two. Considering only these last two rounds, you got a very good approximation of 8.99999951 (i.e., seven more than the answer to the Fiddler, as there were now seven more candidates to be eliminated in those first seven rounds).

Leave it to the Elephant Party to have their crisis unresolved until the very last minute. At least—for this puzzle—a resolution was guaranteed.

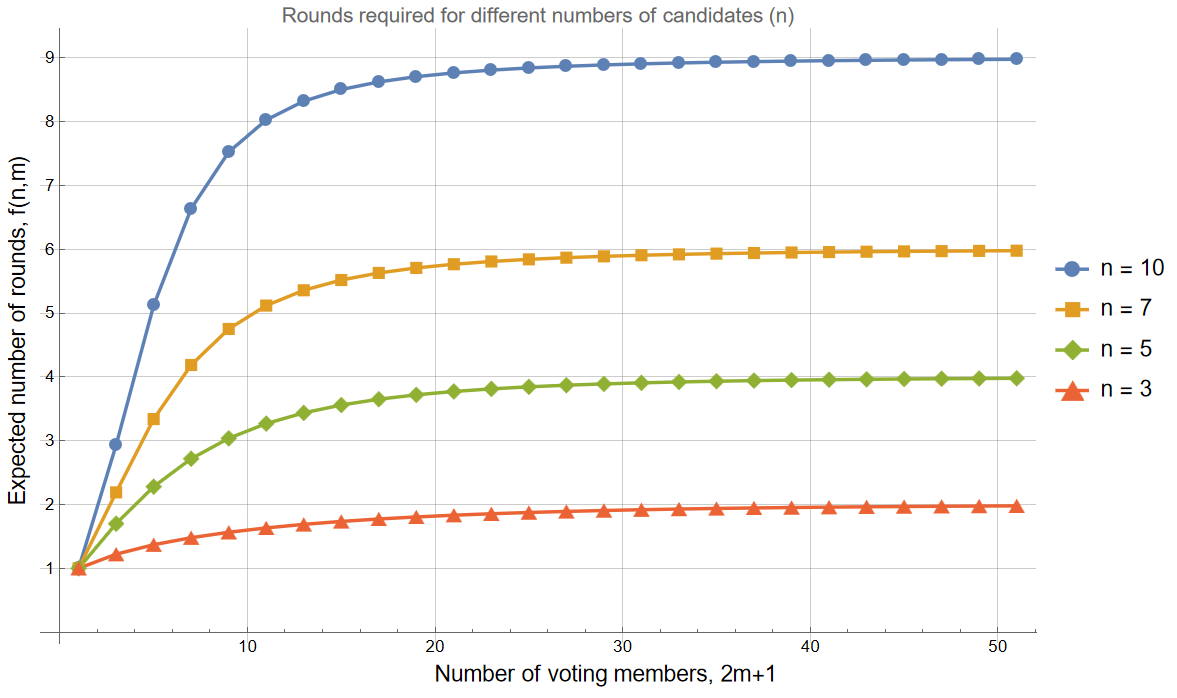
Solver 🎬 Laurent Lessard 🎬 analyzed the more general case in which there were n candidates and 2m+1 voters, as shown below. As m increased, the expected number of rounds appeared to exponentially approach n−1. With as many as 221 voters, then, the results of last week’s puzzle came as no surprise.

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.