How Long Would It Take to Pick a Speaker at Random?
This week, there was more chaos in the House of Representatives. But instead of chaos, what if there had been pure randomness?
Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.
Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.
Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.
I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.
This Week’s Fiddler
The Fiddlerian government is in crisis. In particular, the Elephant Party, which possesses a majority of seats in the House (one of the two congressional chambers), can’t seem to select a new Speaker. At the moment, there are three candidates who want the job.
So here’s their new plan to select a Speaker. All 221 members of the Elephant Party will get in a room and vote for one of the three candidates. Now, the party is known for its chaotic behavior, and sure enough, each voter will pick randomly from among the candidates—even if they themselves are one of the candidates!
If one candidate earns the majority of the votes, they become the next Speaker! Otherwise, the candidate with the fewest votes is eliminated and they repeat the process with one less candidate. If two or more candidates receive the same smallest number of votes, then exactly one of them is eliminated at random.
They might be able to select their speaker in the first round of voting. After a second round, if it occurs, they would definitely have a Speaker. That means the average number of rounds needed is somewhere between one and two. What is this average?
Extra Credit
Uh-oh, a few more candidates have suddenly entered the race! It now appears that there are 10 candidates running for speaker. On average, now how many rounds are needed until one candidate secures a majority of the 221 votes?
Making the Rounds
There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a visual puzzle from Matt Enlow that bothered me, then bothered me again—both times in a good way, of course.
In words, the puzzle goes something like this: You have an infinite supply of hemispherical shells of any radius you want but a maximum radius R. If you stack these shells on top of each other, what’s the tallest tower you can make?
Feel free to make whatever assumptions you want, but I chose to assume that the shells had thickness zero and that all shells had to be facing “up,” meaning each hemisphere’s great circle was resting on the hemisphere below it in the tower.
Last Week’s Fiddler
Congratulations to the (randomly selected) winner from last week: 🎻 Greg Tanner 🎻, from Moorhead, Minnesota. I received 53 timely submissions, of which 26 were correct—a 49 percent solve rate that ranks third-lowest among all Fiddlers.
Last week, you found yourself engaged in a car chase, in which both you and your pursuer were mindful to stop at any and all red lights.
You were trying to make it to the city limit, but you were currently one block ahead of your pursuer, both waiting at red lights. These lights turned green at the same time, at which point both cars began moving east at a speed of one block per minute.
Every time you came to an intersection, there was a 50 percent chance the light was green, in which case you coasted right on through. But there was also a 50 percent chance the light was red, in which case it took exactly one minute for the light to turn green again. These same probabilities governed your pursuer—at each intersection, they had a 50 percent chance of encountering a green light and a 50 percent chance of encountering a red light and having to wait one minute, entirely independent of whatever you might have encountered at that same intersection.
Including the light at which you were now stopped, there were five traffic lights between you and the city limit, as illustrated below. That meant there were six lights for your pursuer.
How likely was it that you’d make it past the city limit without being caught?
Boy, was there a variety of approaches to solving this one. In reading through the solutions, I encountered Markov chains, attempts at solving the “harder” problem of starting N lights away from the city limit with an initial lead of L lights, dynamic programming, binary code … the list goes on.
One way to solve this puzzle was to look at how many red lights you had encountered (excluding the starting light) after one, two, three, and four traffic lights, and compare that to how many red lights your pursuer had encountered after one, two, three, and four traffic lights. If, after any number of these lights, you hit more reds than your pursuer had up to that corresponding number of lights, then you’d be caught. (What’s subtle but important here is that I’m talking about the number of lights rather than the number of minutes that have passed, which would have made things more complicated.)
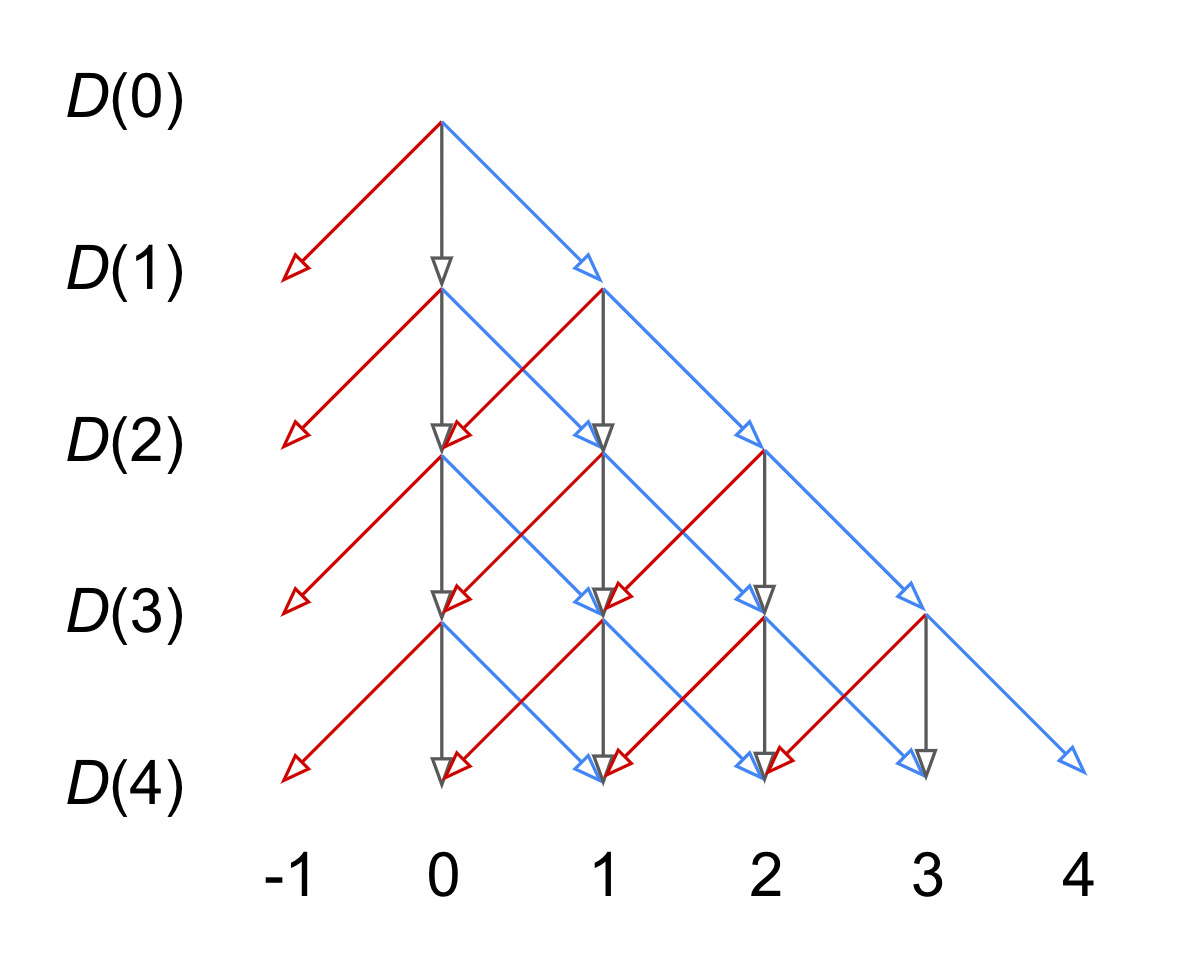
At this point, let’s define the function D(N) as the number of red lights your pursuer has encountered among their first N lights minus the number of red lights you have encountered among your first N lights. Initially, you had D(0) = 0. If any of D(1), D(2), D(3) or D(4) was negative, then you’d get caught.
So how did D evolve as N increased? It behaved like a random walk! When your and your pursuer’s Nth lights were both green upon being encountered, or when they were both red, which together happened 50 percent of the time, D didn’t change. When your Nth light was green but your opponent’s Nth light was red, which happened 25 percent of the time, D increased by 1. But when your Nth light was red and your opponent’s Nth light was green, D decreased by 1. Here’s a diagram showing all the ways D could have evolved:
All the diagonal arrows (shown in red and blue) had probabilities of 25 percent, while the vertical arrows had probabilities of 50 percent. By inspection, there were eight distinct paths down this tree that landed you in the dreaded D = -1 position. Here they were, along with the probabilities of each step in the path:
To find the probability of each path, you had to multiply the probabilities of the independent steps. These products came out to 1/4, 1/8, 1/16, 1/64, 1/32, 1/128, 1/128, and 1/128. Because these eight cases were mutually exclusive, the probability of being caught was the sum of these eight respective probabilities, which was 65/128. That meant the probability of escape was one minus that sum, or 63/128 (about 49.2 percent). At the end of the day, escape was just an inch shy of a coin flip.
Quite a few solvers submitted answers of 838/2,187, or about 38.3 percent. I believe this would have been the answer if each light was randomly red or green after each minute. The wrinkle here was that whenever you encountered a red light, it was guaranteed to be green after one minute, and could not remain red.
Last Week’s Extra Credit
Congratulations to the (randomly selected) winner from last week: 🎻 Jake Conway 🎻, from Grand Rapids, Michigan. I received 31 timely submissions, of which 29 were correct—good for a very solid 94 percent solve rate.
For Extra Credit, you now supposed that Fiddler City was infinitely large. Once again, you found yourself stopped at a red light, heading due east, with your pursuer one block behind you. Both your light and your pursuer’s light turned green the same instant, and all the other details (i.e., speeds, probabilities, and timings) were the same as before.
On average, how many minutes did it take for you to be caught?
While your pursuer inevitably caught you (i.e., with a probability that approached 1 asymptotically over time), the average time to capture was infinite. While paradoxical, this was indeed possible.
Several solvers, including Laurent Lessard and Josh Silverman, showed this using approximations of Catalan numbers. Meanwhile, David Kravitz and Tom Keith demonstrated the absurdity at play using a recursive argument (the latter did so rather comically via a warning in computer code).
Let’s define E(D) as the expected number of lights both you and your pursuer will have to encounter until you have seen more reds than they have, assuming the current difference (i.e., their red lights minus your red lights) is D. Again, our units here are the number of traffic lights, not the number of minutes that have passed. (In the end, this won’t be a problem for us, since the number of minutes for you will always be at least the number of lights encountered.)
In general, E(D) = 1 + 1/4·E(D−1) + 1/2 E(D) + 1/4·E(D+1), with each term corresponding to the probabilities of red vs. green lights outlined above. With a little algebra and a hint of mathematical induction, we can show that E(D) = 2·(D+1) + (D+1)/(D+2)·E(D+1). And with just a little more work, we can show that E(0) = 2·D + 1/(D+1)·E(D). For very large D, E(D) is of course positive, while 2·D grows with D. All this is to say that E(0) diverges.
The bad news? You’re going to get caught. The good news? On average, it will take you infinitely many minutes to get caught. (Want more bad news? The median time to getting caught is still finite. Sorry.)
Want to Submit a Puzzle Idea?
Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.



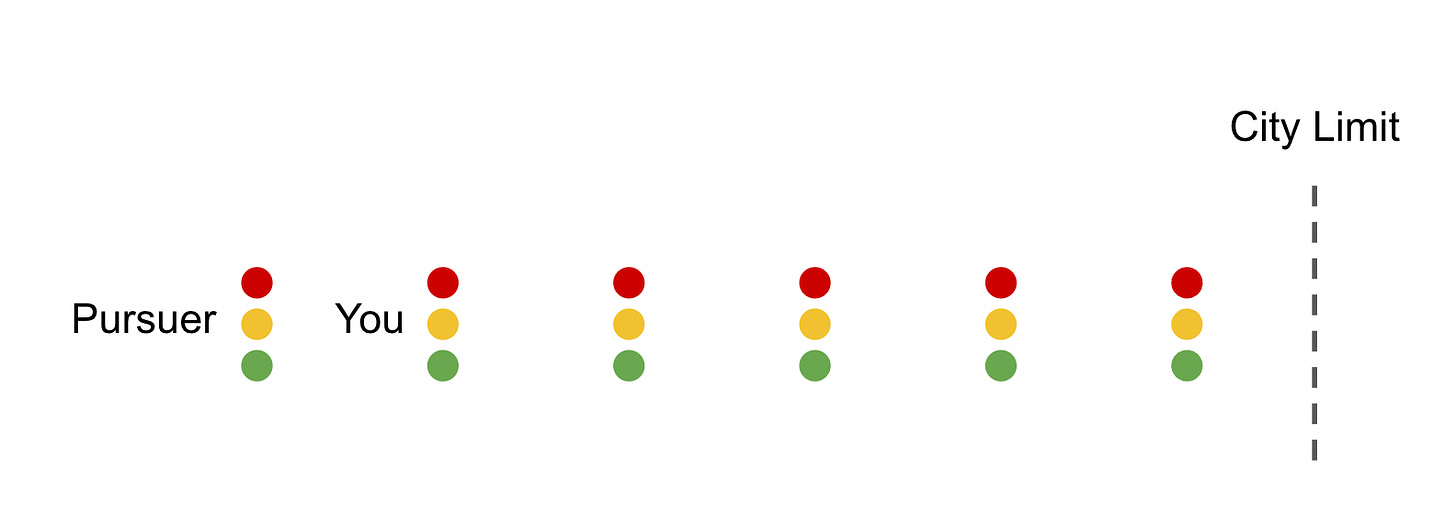

A slight modification to the sphere-stacking problem makes it really interesting! If you have only N spheres, what's the maximum tower height, as a function of N? (because, as JBL noted, with infinite spheres the tower can be made arbitrarily high.)
Spoilers below to my approach for this modification.
First, we can reduce this to stacking semicircles instead of hemispheres, which is equivalent by symmetry, and easier to work with. Also, set the bottom sphere to have R=1. First, I'll consider N=2: one more semicircle, on top of the R=1 one. Let's set it so that it rests on the lower semicircle at an elevation angle of A, i.e. the coordinates of the intersection point are (cos A, sin A). Clearly the radius of the upper semicircle is cos A, and its parametric form is (cos A cos t, cos A sin t + sin A). This is of the form (r*cos t, r*sin t + y0). This y-coordinate is maximized at t = pi/2 with a value of (cos A + sin A). So to solve this for N = 2, we need to pick A to maximize (cos A + sin A). This is simple to do, but let me dig a bit deeper (it'll be useful later). Maximizing (cos A + sin A) is equivalent to picking the point on the unit circle whose Cartesian coordinates sum to a maximum (since a unit circle is parameterized by (cos A, sin A)). This maximum occurs at A = asin(1/sqrt(2)) = pi/4, with a value of 2/sqrt(2).
Okay, on to N = 3. I'll again form the parametric equations for the stacked semicircles. The angle B will define where on the middle semicircle the top semicircle will be placed. From the previous part, the parametric equation for the middle semicircle is (cos A cos t, cos A sin t + sin A), so the point of intersection is at t = B -> (cos A cos B, cos A sin B + sin A). The new semicircle will clearly have radius cos A cos B, and will be shifted vertically up from the origin by a distance of (cos A sin B + sin A). The parameterized y-coordinate will be (cos A cos B) sin t + (cos A sin B + sin A), which is of the form (r*sin t + y0). Anyway, this is obviously maximized at t = pi/2, so now we need to pick A and B to maximize the following:
cos A cos B + cos A sin B + sin A
Now, this looks a lot like the Cartesian definition of spherical coordinates (just with the sines and cosines flipped, which is an equivalent way to parametrize a sphere, just with shifted bounds on the parameters. Proof left as an exercise for the reader). So now, we need to find the point on the unit sphere that maximizes X + Y + Z. Skipping the formal proof, this occurs when X = Y = Z, and so X = Y = Z = 1 / sqrt(3). Solving for A and B, we have A = asin(1/sqrt(3)) and B = asin(1/sqrt(2)) = pi/4, but more importantly, the value of the maximum, and the height of the highest N = 3 stack, is 3 * 1/sqrt(3); the sum of the Cartesian components of that maximizing point on the unit sphere.
The last step here is to demonstrate that increasing N gives an expression for the height of the stack that's equivalent to finding the maximum sum of the Cartesian coordinates of a point on a (N-1)-sphere. This value is N * 1/sqrt(N), or sqrt(N). This is the highest the stack can be with N semicircles, which grows without bound as N -> infinity.
Oh the extra credit is funny because there's a discontinuity at the upper limit, right? Let's say we take a strategy where we always put the new cap with radius c times the old radius (with 0 < c < 1). Then by similarity we have that the height we get in the end satisfies
f(R) = sqrt(R^2 - c^2 R^2) + f(c * R) = R * sqrt(1 - c^2) + c * f(R),
and hence
f(R) = R * sqrt(1 - c^2) / (1 - c) = R * sqrt( (1 + c) / (1 - c) ).
The thing about this function is that it grows to infinity as c approaches 1 from below. So no fixed strategy like this is optimal; instead, we should keep taking successively smaller ratios, and if we do that then our tower will grow without bound.