How Low (or High) Can You Go?

You’re shown random numbers one at a time, and you must guess how each next number will compare to the previous one: Will it be higher or lower? How do your chances of prediction evolve?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. The “Extra Credit” is where the analysis typically gets hairy, or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

From Alex Barnard comes a puzzle about game you can play using nothing but your favorite random number generator:

You’re playing a game of “high-low,” which proceeds as follows:

• First, you are presented with a random number, x₁, which is between 0 and 1.

• A new number, x₂, is about to be randomly selected between 0 and 1, independent of the first number. But before it’s selected, you must guess how x₂ will compare to x₁. If you think x₂ will be greater than x₁ you guess “high.” If you think x₂ will be less than x₁, you guess “low.” If you guess correctly, you earn a point and advance to the next round. Otherwise, the game is over.

• If you correctly guessed how x₂ compared to x₁ then another random number, x₃, will be selected between 0 and 1. This time, you must compare x₃ to x₂, guessing whether it will be “high” or “low.” If you guess correctly, you earn a point and advance to the next round. Otherwise, the game is over.

You continue playing as many rounds as you can, as long as you keep guessing correctly.

You quickly realize that the best strategy is to guess “high” whenever the previous number is less than 0.5, and “low” whenever the previous number is greater than 0.5.

With this strategy, what is the probability you will earn at least two points? That is, what are your chances of correctly comparing x₂ to x₁ and then also correctly comparing x₃ to x₂?

This Week’s Extra Credit

From Alex Barnard also comes some Extra Credit:

Your friend is playing an epic game of “high-low” and has made it incredibly far, having racked up a huge number of points.

Given this information, and only this information, what is the probability that your friend wins the next round of the game?

Making the ⌊Rounds⌉

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I was at it again—doing math while driving. This time, it was Problem 10 from the most recent AIME, an excellent choice by my wife (over in the passenger seat).

The rules of “driver math” are simple: You have to do it all in your head. (Driving is not actually required.) I fell into a few traps on this one, and ultimately resorted to pencil and paper to finish it off once we arrived at our destination. But this problem was a great choice, right on the edge of what I could handle. Give it a go!

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Standings

I’m tracking submissions from paid subscribers and compiling a leaderboard, which I’ll reset every quarter. All correct solutions to Fiddlers and Extra Credits are worth 1 point each. Solutions should be sent prior to 11:59 p.m. the Monday after puzzles are released. At the end of each quarter, I’ll 👑 crown 👑 the finest of Fiddlers. If you think you see a mistake in the standings, kindly let me know.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Adam DeBruler 🎻 from Atlanta, Georgia. I received 63 timely submissions, of which 49 were correct—good for a 78 percent solve rate.

Last time, you were participating in a trail run that ended at sundown at 7 p.m. There were four loops: 1 mile, 3 miles, 3.5 miles, and 4.5 miles. After completing any given loop, you were randomly assigned another loop to run—this next loop could have been the same as the previous one you just ran, or it could have been one of the other three.

Your “score” in the race was the total distance you ran among all completed loops you were assigned. If you were still out on a loop at 7 p.m., any completed distance on that loop did not count toward your score!

It was 5:55 p.m. and you had just completed a loop. So far, you’d been running 10-minute miles the whole way, and you’d maintain that pace until 7 p.m.

On average, what score could you have expected to earn between 5:55 p.m. and 7 p.m.?

There were 65 minutes between 5:55 and 7:00. At a 10 minutes per mile, the most you could have run was 6.5 miles. However, the average was definitely less than this upper bound, since you were often stuck on a loop when it was 7:00.

For convenience, let’s work in units of minutes rather than miles. Then, at the end, we’ll divide our result by 10 to convert back into miles. In minutes, the four loops had durations of 10, 30, 35, and 45.

One approach to this puzzle was to work backwards from 7:00. Suppose you had just finished a loop at 7:00. You were about to be assigned another loop—but time was up! How many more minutes could you expect to run? Zero.

Next, let’s jump back to 6:55. (Five-minute intervals made sense here because all the times and loop durations were multiples of five.) If you had just finished a loop at 6:55, how many more minutes could you expect to run? Since all four loops required more than 5 minutes, you couldn’t have completed any of them. That still meant you could expect zero more minutes worth of completed loops.

At 6:50, things got a little more interesting. If you were randomly assigned the 10-minute loop, then you’d run for 10 minutes. But if you were assigned any of the other three loops, you wouldn’t have completed them in time. Therefore, you had a 25 percent chance of running another 10 minutes, for an average of 2.5 minutes. And the same was true for 6:45. You had a 25 percent chance of running another 10 minutes, for an average of 2.5 minutes.

If you finished a loop at 6:40, you had a 25 percent chance of running a 10 minute loop, for an expectation of 2.5 minutes. And within that 25 percent case, you could expect to run another 2.5 minutes between 6:50 and 7:00. In total, your expected time running was 2.5 + 0.25·(2.5) = 3.125 minutes. And the same was true at 6:35.

But once you worked your way back to 6:30, the math started getting hairy. That was because finishing a loop at 6:30 meant you could now accrue minutes via the 10-minute loop as well as the 30-minute loop. To help organize your thinking, a better strategy was called for than analyzing 5-minute intervals.

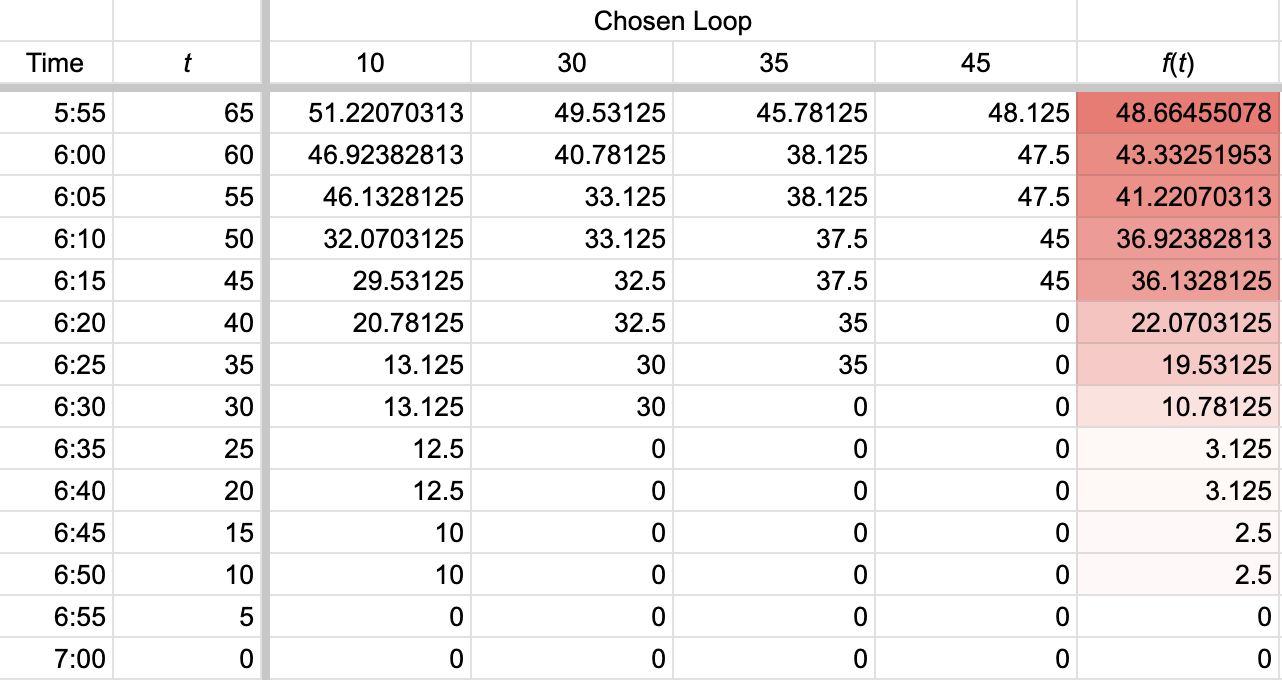
One such strategy was recursion. In particular, let f(t) represent the expected remaining running time when you have completed a loop precisely t minutes before 7:00. Thus, the goal of the problem was to evaluate f(65). Since you had a 25 percent chance of picking the 10-, 30-, 35-, and 45-minute loops, the following recursion relation was true:

\(f(t) = \frac{10+f(t−10)}{4} + \frac{30+f(t−30)}{4} + \frac{35+f(t−35)}{4} + \frac{45+f(t−45)}{4}\)

However, it should be noted that each of the four terms on the right was zero when the input of the function f was less than zero.

With the recursion relation in hand, you could work backwards—whether by coding, spreadsheet, or hand—to calculate f(65). In the screenshot from a spreadsheet below, f(65) appears atop the rightmost column.

You could expect to run roughly another 48.66 minutes. The exact time was 99665/2048 minutes. Dividing by 10 to convert that figure back into miles, you could expect to run another 19933/4096, or about 4.866 miles. That was a shade under 75 percent of the maximum 6.5 miles you had time for. (I accepted any answer that was sufficiently close to 4.866 miles.)

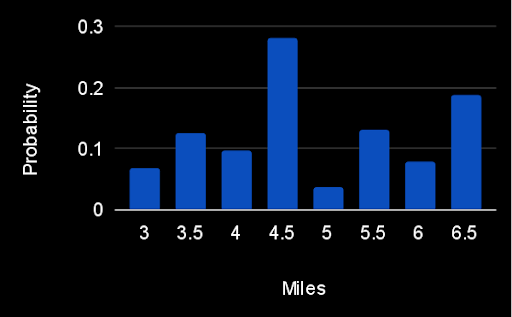
Solver 🎬 Tom Singer 🎬 produced a distribution of how many miles you’d complete in the 65 minutes you had:

There were a few different ways to run the maximum of 6.5 (i.e., 6.5 = 3.5 + 3 = 3.5 + 1 + 1 + 1 = 4.5 + 1 + 1). Meanwhile, the minimum was 3 miles, which occurred when you were first assigned the 3-mile loop (or thrice assigned the 1-mile loop), followed by the 4.5-mile loop. Sure enough, the average appeared to be about 4.866 miles.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 David Slater 🎻 from Okemos, Michigan. I received 35 timely submissions, of which 22 were correct—good for a 63 percent solve rate.

This time, there was one more wrinkle. At some point during the race, if you were unhappy with the loop you had just been randomly assigned, you were granted a “mulligan,” allowing you to get another random assignment. (Note that there was a 25 percent chance you’d be assigned the same loop again.) You didn’t have to use your mulligan, but you couldn’t use it more than once.

As before, the time was 5:55 You had just completed a loop, and you hadn’t used your mulligan yet.

With an optimal strategy (i.e., using the mulligan at the right moment, if at all), on average, what score could you have expected to earn between 5:55 and 7:00?