How Far Can You Run Before Sundown?

You’re racing against the clock … and fate. As you’re randomly assigned one of four looping trails, how far can you expect to run?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. The “Extra Credit” is where the analysis typically gets hairy, or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

Note: Due to the upcoming holiday, the next edition of Fiddler on the Proof will be coming out on September 5, 2025.

This Week’s Fiddler

From Ryan Goldenberg comes a puzzle inspired by an actual race he completed!

You’re participating in a trail run that ends at sundown at 7 p.m. There are four loops: 1 mile, 3 miles, 3.5 miles, and 4.5 miles. After completing any given loop, you are randomly assigned another loop to run—this next loop could be the same as the previous one you just ran, or it could be one of the other three. Being assigned your next loop doesn’t take a meaningful amount of time; assume all your time is spent running.

Your “score” in the race is the total distance you run among all completed loops you are assigned. If you’re still out on a loop at 7 p.m., any completed distance on that loop does not count toward your score!

It is now 5:55 p.m. and you have just completed a loop. So far, you’ve been running 10-minute miles the whole way. You’ll maintain that pace until 7 p.m.

On average, what score can you expect to earn between 5:55 p.m. and 7 p.m.?

This Week’s Extra Credit

From Ryan Goldenberg also comes some Extra Credit:

Now let’s add one more wrinkle. At some point during the race, if you’re unhappy with the loop you’ve just been randomly assigned, you’re granted a “mulligan,” allowing you to get another random assignment. (Note that there’s a 25 percent chance you’ll be assigned the same loop again.) You don’t have to use your mulligan, but you can’t use it more than once.

As before, the time is 5:55 p.m. You have just completed a loop, and you haven’t used your mulligan yet.

With an optimal strategy (i.e., using the mulligan at the right moment, if at all), on average, what score can you expect to earn between 5:55 p.m. and 7 p.m.?

Making the ⌊Rounds⌉

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a new (to me, at least) logic game from The New York Times: Pips. It has a KenKen feel, but the catch is that you’re placing two conjoined numbers—that is, dominoes—at a time. (The dots on dominoes are called “pips,” hence the name.)

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Standings

I’m tracking submissions from paid subscribers and compiling a leaderboard, which I’ll reset every quarter. All correct solutions to Fiddlers and Extra Credits are worth 1 point each. Solutions should be sent prior to 11:59 p.m. the Monday after puzzles are released. At the end of each quarter, I’ll 👑 crown 👑 the finest of Fiddlers. If you think you see a mistake in the standings, kindly let me know.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Tyler Bootz 🎻 from Maize, Kansas. I received 53 timely submissions, of which 32 were correct—good for a 64 percent solve rate. This was a tricky one!

Last week, a casino offered you $55 worth of “free play vouchers.” You specifically received three $10 vouchers and one $25 voucher.

You could play any or all vouchers on either side of an even-money game as many times as you wanted (or could). You kept the vouchers wagered on any winning bet and got a corresponding cash amount equal to the vouchers for the win. But you lost the vouchers wagered on any losing bet, with no cash award. Vouchers couldn’t be split into smaller amounts, and you could only wager vouchers (not cash).

What was the guaranteed minimum amount of money you could surely win, no matter how bad your luck? And what betting strategy always got you at least that amount?

Hint: You could play vouchers on both sides of the even money game at the same time!

A good strategy was to play two roughly equal vouchers against each other. I’m old enough to remember the tagline for the film, Alien vs. Predator: “Whoever wins … we lose.” This was quite the opposite—whichever voucher loses, you win!

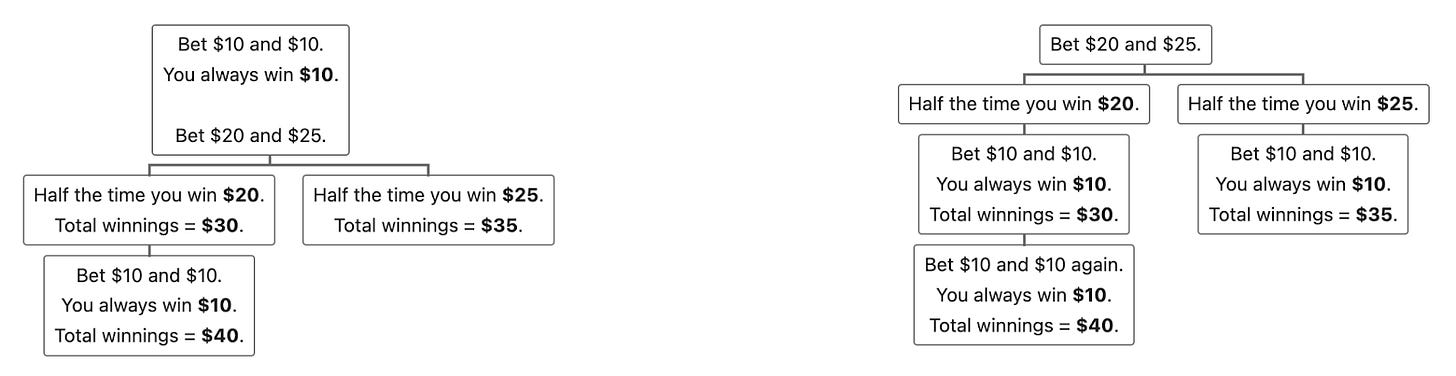
For convenience, let’s call the vouchers V10 and V25, as opposed to real money, which we’ll indicate using dollar signs. You could start by playing two V10s against each other. After the first game, you lost one of the V10s but converted it into $10. At this point, you had two V10s, a V25, and $10. If you wagered your remaining two V10s against each other, you were left with one more V10, your V25, and $20. Finally, you could play your V10 against your V25. You could have won $25, but in the worst-case scenario you only won $10. Now all you had left was a V25 and $30. With no more vouchers to play your V25 against, $30 was the most money you could win. The most you could win from that strategy, I should say.

But it was possible to do better! While playing the evenly matched V10s against each other was a sensible move, it essentially wasted the V25. If you had replaced the V25 with, say, a fourth V10, that strategy would still have netted you $30.

So let’s put that V25 to better use. One way was to play it right at the beginning. If you played two V10s against the V25 in the first game, then there were two possibilities:

• The V10s won and you lost the V25. At this point, you had three V10s and $20. Playing the V10s against each other one at a time, you were guaranteed another $20. In total, you were guaranteed $40.

• The V25 won and you lost the V10s. At this point, you had one V10, the V25, and $25. Playing the remaining V10 against the V25 netted you another $10 guaranteed, for a total of $35.

So no matter what, you made at least $35, which was the solution.

You could also have arrived at the same result by holding on to the V25 until the second game. In the first game you played two V10s against each other, after which you had two V10s, the V25, and $10. At this point, you played the remaining two V10s against the V25. Either you made $25 and were left with a V25 that earned no further guaranteed money (for a total of $35), or you made $20 and were left with two V10s that earned an additional guaranteed $10 (for a total of $40).

Solver 🎬 Rohan Lewis 🎬 made some handy-dandy diagrams that illustrated these two optimal strategies:

Finally, what if you were allowed to wager cash alongside vouchers? While the puzzle said vouchers couldn’t be split up, let’s assume the cash could be split into smaller denominations. The short answer was that it was now possible to convert all your vouchers into cash, earning you a guaranteed $55. If you submitted an answer of $55 under the assumption that you could wager cash—something that wasn’t clearly stated in the original statement of the puzzle—I still awarded credit.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Derek Nagel 🎻 from Savage, Minnesota. I received 31 timely submissions, of which 15 were correct—good for a 48 percent solve rate. Tricky, again!

For Extra Credit, you had the same $55 worth of vouchers from the casino in the same denominations. But this time, you weren’t interested in guaranteed winnings. Instead, you set your betting strategy so that you’d have at least a 50 percent chance of winning W dollars or more. As before, you couldn’t split vouchers.

What was the maximum possible value of W? In other words, what was the greatest amount of money you could have at least a 50 percent chance of winning from the outset, with an appropriate strategy? And what was that betting strategy?