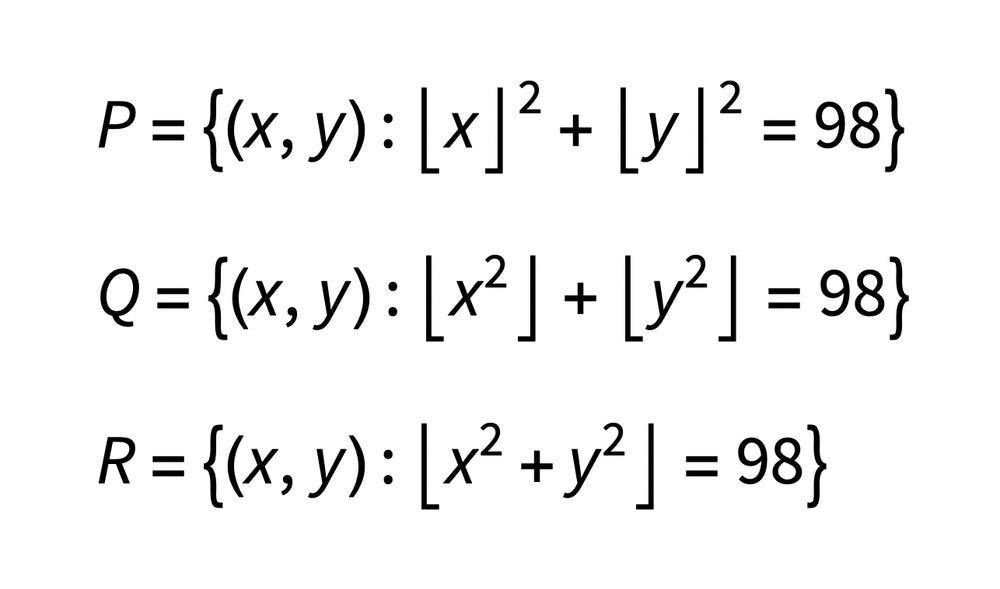How Greedily Can You Mow the Lawn?

You’re trying to mow a circular patch of lawn with straight passes of your lawnmower. If you mow as much of the remaining grass as possible with each pass, how long will it take you to finish?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “Extra Credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

You’re mowing a circular lawn with a radius of 1 unit. You can mow in straight strips that are 1 unit wide.

The fewest number of passes you would need to mow the entire lawn is two, as shown below. In one pass (shown in blue) you can mow half the circle, and in the second pass (shown in red) you can mow the other half of the circle.

However, instead of minimizing the number of passes, you greedily choose how to orient each pass so it cuts as much of the unmowed grass as possible. A pass doesn’t have to go through the center of the circle and can be in any direction, but must be straight and cannot bend.

With this “greedy” approach, how many passes will it take for you to mow the entire lawn?

This Week’s Extra Credit

Instead of mowing a two-dimensional lawn, now you’re boring cylinders through a three-dimensional unit sphere. Each cylinder has a diameter of 1 (and a radius of 1/2).

Once again, you are greedily choosing the orientation of your boreholes so that they carve out as much of the remaining sphere as possible with each pass.

With this “greedy” approach, how many passes will it take for you to pulverize the entire sphere?

Making the ⌊Rounds⌉

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a delightful post from Matt Enlow, which I’ll paraphrase here:

Each of the following relations below has a positive area in the coordinate plane. Which has the greatest area? Which has the least area? How do you know? And what is the area of each region?

I’ve got a pretty good handle on the areas of P and R, and find Q to be the most interesting of the three.

As always, feel free to share your thinking in the comments below, or respond to Matt’s original post.

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Standings

I’m tracking submissions from paid subscribers and compiling a leaderboard, which I’ll reset every quarter. All timely correct solutions to Fiddlers and Extra Credits are worth 1 point each. At the end of each quarter, I’ll 👑 crown 👑 the finest of Fiddlers. (If you think you see a mistake in the standings, kindly let me know.)

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Travis 🎻 from Atlanta, Georgia. I received 82 timely submissions, of which 74 were correct—good for a 90 percent solve rate.

Last week, I was experimenting with different strategies in a 5000-meter race (known as a “5K”). If I had run the distance at a steady pace, I would have finished in precisely 23 minutes.

However, knowing I’d have a burst of energy near the finish line, I intentionally started out with a slower, 24-minute pace (i.e., running at a speed such that if I ran the whole distance at that speed, I’d finish in 24 minutes). Halfway through the race by distance (i.e., after 2500 meters), I increased my speed by 10 percent. Three-quarters of the way through, I increased by another 10 percent. If you’re keeping track, that was 21 percent faster than my speed at the start.

I continued in this fashion, upping my speed by 10% every time I was half the distance to the finish line from my previous change in pace. (Let’s put aside the fact that my speed would have surpassed the speed of light somewhere near the finish line.)

Using this strategy, how long would it have taken me to complete the 5K?

One approach was to figure out how long each segment of the race—the first half, the next quarter, the next eighth, and so on—took to run, and then add all these times up. If my speed hadn’t deviated from its initial value, these times would have summed to 24 minutes. Because I kept increasing my speed with each interval, my total time had to be something less than 24 minutes. But how much less? Let’s find out!

Let’s call my initial speed v. Since we said this initial speed would have completed the 5000 meters in 24 minutes, v = 5000/24 meters per minute, or about 208.3 meters per minute.

Now, how long did it take to run the first half of the race (by distance)? Speed equals distance divided by time, which means that time equals distance divided by speed. The distance of the first half was 2500 meters and we said my initial speed was v, so the time it took was 2500/v.

What about the next quarter of the race? That distance was 1250 meters, and the speed was 10 percent greater, or 1.1v. The time required to run this segment was therefore 1250/(1.1v).

And the next eighth? That distance was 625 meters, and the speed was another 10 percent greater, or 1.1²v. The time required to run this segment was 625/(1.1²v).

This pattern continued, with each segment half as long as the previous one, but run at a speed that was 10 percent greater. Adding up the times, we get the infinite series 2500/v + 1250/(1.1v) + 625/(1.1²v) + …, which was a geometric series in which each term was 1/2.2 (or 5/11) of the previous term. With an initial term of 2500/v, the sum came to 2500/v/(1−5/11) = 2500/v · 11/6 = 13750/(3v).

Finally, we can plug in 5000/24 for the value of v, noting that we were careful to use units of meters and minutes throughout, so our final result would indeed be in minutes. We have 13750/(3v) = 13750/3 · 24/5000 = 22. So with this strategy, I’d finish the race in exactly 22 minutes. I was pleased to note that this was faster than my “even split” strategy of 23 minutes. However, this “negative split” strategy required me to run faster than the speed of light at the tail end of the race, a feat that sounded equally painful and improbable.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Chris Payne 🎻 from Arlington, Virginia. I received 59 timely submissions, of which 45 were correct—good for a 76 percent solve rate.

Upping my tempo in discrete steps was such a slog. Instead, I concocted a new plan in which I continuously increased my pace in the following way:

At the beginning of the race, I started with a 24-minute pace. Then, wherever I was on the race course, I always ran 10 percent faster than I was when I was twice as far from the finish line. Also, my speed was always increasing in a continuous and smooth fashion.

Using this strategy, how long would it have taken me to complete the 5K?