Can You Race Against Zeno?

You run half a race, then speed up a little. You run half of the remainder, then speed up a little more. If you keep doing this, how fast will you run the entire race?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “Extra Credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

I’ve been experimenting with different strategies in 5000-meter races (known as “5K”s). If I run the distance at a steady pace, I’ll finish in precisely 23 minutes.

However, I tend to find a burst of energy as I near the finish line. Therefore, I’ve tried intentionally running what’s called a “negative split,” meaning I run the second half of the race faster than the first half—as opposed to a “positive split,” where I run a slower second half.

I want to take the concept of a negative split to the next level. My plan for an upcoming race—the “Zeno Paradox 5K”—is to start out with a 24-minute pace (i.e., running at a speed such that if I ran the whole distance at that speed, I’d finish in 24 minutes). Halfway through the race by distance (i.e., after 2500 meters), I’ll increase my speed (i.e., distance per unit time) by 10 percent. Three-quarters of the way through, I’ll increase by another 10 percent. If you’re keeping track, that’s now 21 percent faster than my speed at the start.

I continue in this fashion, upping my speed by 10% every time I’m half the distance to the finish line from my previous change in pace. (Let’s put aside the fact that my speed will have surpassed the speed of light somewhere near the finish line.)

Using this strategy, how long will it take me to complete the 5K? I’m really hoping it’s faster than my steady 23-minute pace, even though I start out slower (at a 24-minute pace).

This Week’s Extra Credit

I still want to run a negative split, but upping my tempo in discrete steps is such a slog. Instead, my next plan is to continuously increase my pace in the following way:

At the beginning of the race, I’ll start with a 24-minute pace. Then, wherever I am on the race course, I’m always running at a 10 percent faster speed than I was when I was twice as far from the finish line. Also, my speed should always be increasing in a continuous and smooth fashion.

(On the off chance you find more than one speed as a function of distance that satisfies all these conditions, I’m interested in seeing how. If only one such function exists, can you prove it? Regardless, my expectation is for the function to be as straightforward as possible.)

Using this strategy, how long will it take me to complete the 5K? Once again, I’m hoping it’s faster than my steady 23-minute pace, even though I started out slower.

Making the ⌊Rounds⌉

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a book! (And I believe this is my first time doing so.) I’m about 300 pages into Jordan Ellenberg’s “Shape,” and it’s a banger. Now, I’m not quite following how the book is structured—it freely floats from one mathematical idea or anecdote to another along the lines of, “that reminds me of….” That said, all these ideas and anecdotes are clearly communicated and often hilariously presented.

In particular, there’s a wonderful explanation of Fermat’s Little Theorem and its importance that makes me wish I had paid more attention in number theory class. (No offense, number theorists!) And there are even some solid puzzles left as exercises to the reader, like the footnote on page 295.

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Standings

I’m tracking submissions from paid subscribers and compiling a leaderboard, which I’ll reset every quarter. All timely correct solutions to Fiddlers and Extra Credits are worth 1 point each. At the end of each quarter, I’ll 👑 crown 👑 the finest of Fiddlers. (If you think you see a mistake in the standings, kindly let me know.)

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Scott Lefton 🎻 from San Antonio, Texas. I received 41 timely submissions, of which 38 were correct—good for a 93 percent solve rate.

Last week, you started by drawing a unit circle (i.e., a circle with radius 1). Then you drew another unit circle whose center was not inside the first one. Then you drew a third unit circle whose center was not inside either of the first two. You kept doing this until you had drawn a total of seven circles.

Considering the entire region that was inside at least one of the circles, what was the minimum possible area of this region?

Let’s take this one circle at a time, shall we? With one circle, the only possible area you could have was that of one circle, which was 𝜋. With two circles, minimizing the area meant placing the center of the second circle anywhere on the circumference of the first:

With three circles, you could minimize the total area by placing the center at either of the two locations where the first two circles intersected:

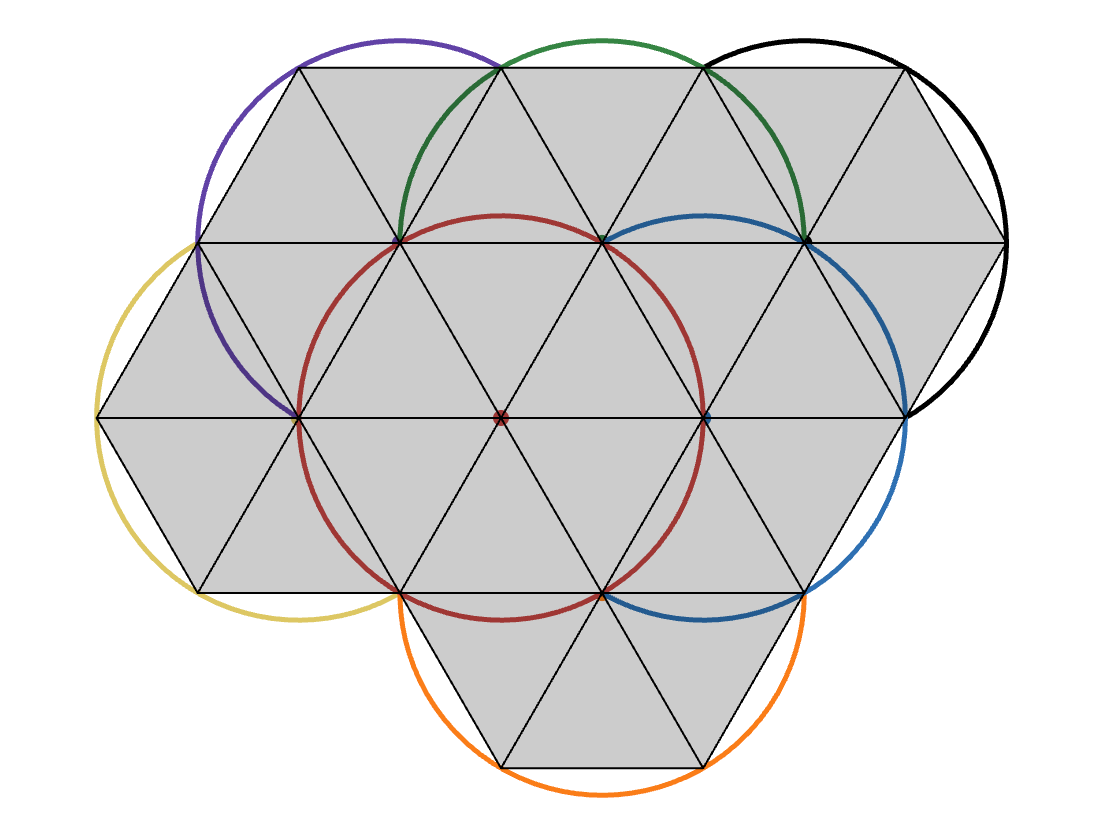
At this point, the overall shape had three cusps. It was tempting to place the next three centers at those three cusps, resulting in the following figure:

But now, placing the seventh and final circle meant making the figure asymmetric. Centering that last circle at one of the six new cusps gave you this:

What was the area of this shape? One way to figure this out was to partition the figure into equilateral triangles and circular segments:

There were 25 equilateral triangles with side length 1, each of which had an area of √(3)/4—something you could show with a smidge of trigonometry. Meanwhile, there were 13 circular segments along the periphery of the figure. Each such circular segment had an area that was the difference between one-sixth of a circle, with area 𝜋/6, and a unit equilateral triangle, whose area we already said was √(3)/4.

Putting this all together, the total area of the figure was 25·(√(3)/4) + 13·[𝜋/6−√(3)/4]. This simplified to 3√3 + 13𝜋/6, or about 12.003.

But alas, that was not the answer. Why? Because we got a little too greedy in placing the fourth, fifth, and sixth circles all at once on the three available cusps. Looking at the figure above, there was a new, very attractive cusp in the bottom left where adding another circle didn’t increase the total area by much. Moving the circle from the top right into that slot resulted in a hexafoil configuration with a reduced total area:

Now there were just 24 equilateral triangles and 12 circular segments. That meant the total area was 24·(√(3)/4) + 12·[𝜋/6−√(3)/4]. This simplified to 3√3 + 2𝜋, or about 11.479. That was a full sixth of a unit circle less than our previous attempt, and was indeed the smallest possible area—and the solution to the puzzle!

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Josh Arnold 🎻 from Arlington, Massachusetts. I received 33 timely submissions, of which 29 were correct—good for an 88 percent solve rate.

Instead of seven unit circles, you drew N of them. As before, the center of each new circle you drew couldn’t be inside any of the previous circles.

Considering the entire region that was in at least one of the circles, what was the minimum possible area of this region as N got very, very large?