Don’t Flip Out!

“Heads I win, tails you lose” isn’t the only unfair coin flip. It turns out there’s a whole family of them.

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

From Julien Beasley and Kyle Miller comes a confounding coin conundrum:

Kyle and Julien are playing a game in which they each toss their own fair coins. On each turn of the game, both players flip their own coin once.

If, at any point, Kyle’s most recent three flips are Tails, Tails, and Heads (i.e., TTH), then he wins. If, at any point, Julien’s most recent three flips are Tails, Tails, and Tails (i.e, TTT), then he wins.

However, both players can’t win at the same time. If Kyle gets TTH at the same time Julien gets TTT, then no one wins, and they continue flipping. They don’t start over completely or erase their history, mind you—they merely continue flipping, so that one of them could conceivably win in the next flip or two.

What is the probability that Kyle wins this game?

Extra Credit

Kyle and Julien write down all eight possible sequences for three coin flips (HHH, HHT, HTH, THH, HTT, THT, TTH, and TTT) on eight different slips of paper. They place these slips into a hat and shake it.

They will each randomly draw slips of paper out of the hat, at which point they will play the same game as previously described, but looking for the sequence specified on the slip of paper they each selected. Kyle draws first and looks at his slip of paper. After doing some calculations, he says: “Well, at this point, it’s about as fair a match as it could possible be.” 

Which slip or slips of paper might Kyle have drawn? And what are his chances of winning at this point (i.e., before Julien selects his own slip of paper)?

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. Once again, I’m sharing Mathigon’s annual puzzle calendar, curated by my colleague Eda Aydemir. A new puzzle is being posted every day during the month of December.

This week, I’m sharing the puzzle from Dec. 9, which asks if you can cut a right triangle with legs of length 1 and 2 into five identical triangles, each similar to the original triangle.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Eric Bill 🎻 from Endicott, New York. I received 90 timely submissions, of which 73 were correct—good for an 81 percent solve rate.

In the game Connections, there are 16 words that must be arranged by you, the player, into four distinct sets of four words each, where the words in each set have some common property. Each turn, you must select four remaining words and press the “Submit” button. If they indeed represent one of the four sets, they are removed and you must try to find another set among the remaining words. The game ends when you have correctly identified all four sets.

Importantly, the game also gives you hints. Anytime your four selected words include exactly three from a correct set, you are told that your selection is “One away…” from a correct set, meaning just one of your four choices was incorrect.

When first presented with all 16 words, suppose you picked four words at random. What was your probability of seeing the “One away…” message?

This puzzle was an exercise in combinatorics. The solution was a fraction whose denominator represented all the ways to choose four words out of the 16, while the numerator was all the ways to choose four words such that exactly three of them were in the same set.

Let’s tackle the denominator first. How many ways were there to choose four words out of 16? Indeed, there were 16 choose 4 such ways! More explicitly, that number was (16·15·14·13) / (4·3·2·1). If you’re new to combinatorics, you can arrive at that expression by picking one from among 16 words, then one from among the 15 remaining words, then one from among the 14 remaining words, and finally one from among the 13 remaining words. Since you can choose the words in any order, that means you’ve overcounted by a factor of 4!, hence the division. In any event, the denominator turned out to be 1820.

As is typical of these sorts of problems, determining the numerator was the trickier part. Here was one way to think about it:

• First, choose one set from among the four to pick three words from. There were four ways to choose this set.

• Then, choose three words from within this set. Equivalently, you could have chosen the one word that you didn’t include from this set. Either way, there were four ways to do this.

• Finally, choose your fourth word from the remaining 12 words (in those other three sets).

Putting these steps together meant the numerator was 4·4·12, or 192. (Several readers missed one of those factors of 4, which meant their answer was four times too small.)

In the end, the probability was 192/1820, which simplified to 48/455, or about 10.55 percent. A few solvers commented this likelihood was higher than they had initially expected. I, for one, agree!

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Ivor Traber 🎻 from Waterloo, Ontario, Canada. I received 22 timely submissions, of which 15 were correct—good for a 68 percent solve rate. As a matter of fact, this puzzle garnered the second-fewest correct submissions among all Fiddlers and Extra Credits. It was a toughie!

In the game of Connections, suppose you had already identified two sets in your first two guesses, leaving you with eight remaining words. However, at this point, you had absolutely no idea what the remaining two sets might have been.

Nevertheless, with some clever strategizing—and by taking advantage of the “One away…” messages the game provides—it was possible to determine those remaining two sets in a relatively small number of guesses. (The real game affords you only four incorrect guesses, but for the purposes of this puzzle, we ignored that fact and supposed that you have an unlimited number of guesses.)

Using your cleverest strategy, how many guesses did you need to be certain that you could always solve this puzzle, even in a worst-case scenario?

Before finding an exact answer like this, I like to begin by putting some bounds on it. First off, what was the answer at most?

There were eight words remaining, which meant there were 8 choose 4 (or 70) ways to pick four words. At this point, once you guessed a group of four words, whatever feedback you got also applied to their complement (i.e., the remaining four words). For example, if you picked four words such that three were in one set and one was in another, then the same could be said about the four words you didn’t pick. To simplify things, you could instead consider the 7 choose 3 (or 35) groups that included a particular word.

And so, in an absolute worst case scenario, you could guess all 35 of these groups, only to find the correct set on your 35th guess. After that, you could easily identify the remaining four words as the final set on your 36th guess. That meant the answer was at most 36. Of course, we haven’t yet leveraged any of the “One away…” messages, so the answer was likely to be quite a bit less.

So much for the upper bound. What about a lower bound on the answer? What number of guesses was the answer at least?

After every guess, there were three possibilities: Either (1) you correctly identified a set, (2) you were “One away…” from a set, or (3) your group had two words from one set and two words from the other. In other words, your guesses formed a binary decision tree, with branches in one direction representing being “One away…” and branches in the other direction representing being two away. Your goal was to find the shortest possible tree that contained all 35 potential groups in the nodes of the tree.

Now, a binary tree that’s five levels (or guesses) deep contains up 31 nodes (i.e., 2⁰ + 2¹ + 2² + 2³ + 2⁴ = 31) , which didn’t have enough room for 35 possible groups. That meant you would need at least six guesses to identify the first set. After that, you needed one more guess to confirm the final set, which meant the lower bound was seven guesses.

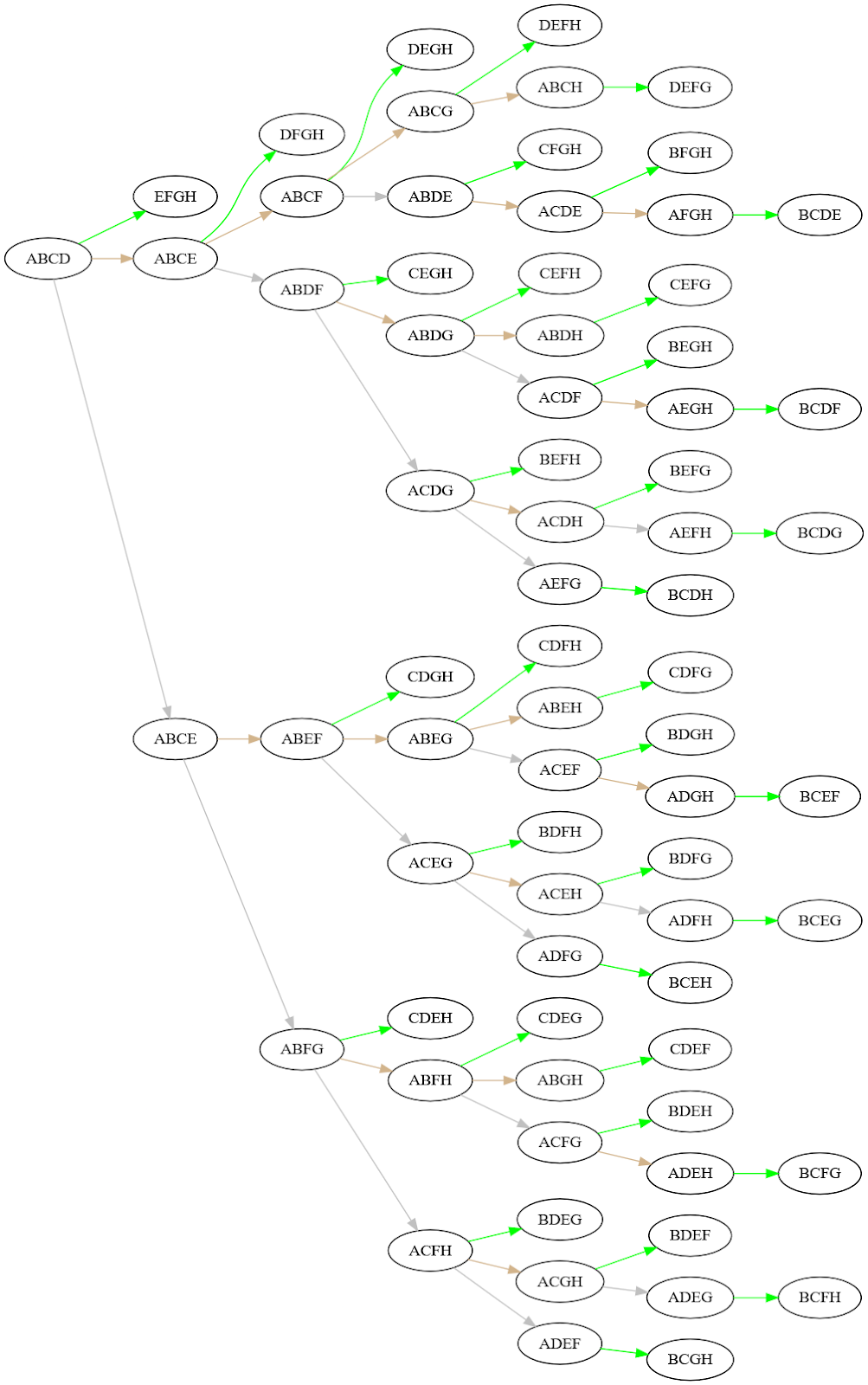
Many solvers proved that seven guesses wasn’t only the lower bound, but that it was indeed the answer. Solver 🎬 Izumihara Ryoma 🎬 diagrammed one such optimal guessing strategy as a binary tree, having labeled the eight words with the letters A through H:

This tree can be read from left to right. If a guess was correct, you followed the green arrow to guess the final set among the remaining four words. If you were told your guess was “One away…,” you followed the tan arrow for your next guess; otherwise, you followed the gray arrow for your next guess. Sure enough, by your 7th guess (if you made it that far), you were guaranteed to have identified all the sets.

By the way, some solvers gave an answer of six instead of seven, not bothering to include the final guess when there were only four words remaining. A few others said you needed five guesses to know what the two sets actually were, not bothering to include the final two guesses needed to submit them. As long as the explanations were present—and they generally were—I marked these answers as correct.

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.