Can You Make the Connection?

Once again, we find ourselves at the intersection of wordplay and mathematical puzzles. It’s a wonderful place to be.

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

From Bart Wright comes a puzzle about a new game from The New York Times, Connections:

In Connections, there are 16 words that must be arranged by you, the player, into four distinct sets of four words each, where the words in each set have some common property. Each turn, you must select four remaining words and press the “Submit” button. If they indeed represent one of the four sets, they are removed and you must try to find another set among the remaining words. The game ends when you have correctly identified all four sets.

Importantly, the game also gives you hints. Anytime your four selected words include exactly three from a correct set, you are told that your selection is “One away…” from a correct set, meaning just one of your four choices was incorrect.

When first presented with all 16 words, suppose you pick four words at random. What is your probability of seeing the “One away…” message?

Extra Credit

From Dean Ballard comes another puzzle about Connections that was suggested to Dean by Zach Shiner (Team Zach for the win!).

Suppose you already identified two sets in your first two guesses, leaving you with eight remaining words. However, at this point, you have absolutely no idea what the remaining two sets might be.

Nevertheless, with some clever strategizing—and by taking advantage of the “One away…” messages the game provides—it’s possible to determine those remaining two sets in a relatively small number of guesses. (The game affords you only four incorrect guesses, but for the purposes of this puzzle, let’s ignore that fact and suppose that you have an unlimited number of guesses.)

Using your cleverest strategy, how many guesses would you need to be certain that you could always solve this puzzle, even in a worst-case scenario?

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. As the holiday season is already upon us (Happy Hanukkah to those who celebrate!), I’m sharing Mathigon’s annual puzzle calendar, curated by none other than my colleague Eda Aydemir! A new puzzle is being posted every day during the month of December. So far, this year’s puzzles have ranged from combinatorics to chess to aperiodic monotiles.

This week, I’m sharing the puzzle from Dec. 1, which had a rather surprising result when you thought about it rationally:

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Hazel 🎻 from Maine. I received 76 timely submissions, of which 72 were correct—good for an astounding 95 percent solve rate. Nice work, everyone!

Last week’s puzzle was about the fictional board game of Oligopoly. Like Monopoly, it consisted of a square board with 40 individual spaces around it, numbered from 0 to 39. All players began on space 0 (akin to the “Go” square in Monopoly) and rolled a pair of dice to determine how many spaces they advanced each turn. However, unlike Monopoly, there was no way to otherwise advance around the board (i.e., there was no “Chance,” “Community Chest,” going to jail, etc.).

In their first pass around the board, which space from 1 to 39 were players most likely to land on at some point (i.e., not necessarily on their first or last roll, but after any number of rolls)?

After one roll, landing on 7 was the most likely, with a probability of 1/6. But that wasn’t necessarily the answer to this puzzle, since there were quite a few ways to land on many of the other spaces as well. For example, to land on 8, a player could have initially rolled an 8, with a probability of 5/36. Or, they could have rolled a 2 (i.e., snake eyes) and then a 6, with a combined probability of 1/36 · 5/36. Or they could have rolled a 3 and then a 5, and so on. It could even have taken more than two rolls, such as with a 2, then a 3, and then another 3.

Because you could wind up at the same space after varying numbers of rolls, it was difficult to calculate the probability of landing on a given square outright. As a result, several solvers turned to their computers and simulated thousands or even millions of games of Oligopoly, thereby revealing which spaces were more likely to be landed on.

Another approach was to calculate the probabilities of landing on earlier spaces, and then use those values to (recursively or dynamically) calculate the probabilities of landing on later spaces. Let’s use such an approach to compute p_n, the probability of landing on space n (including n = 0) at some point during the first trip around the board.

We knew p₀ = 1, since everyone started on “Go.” Let’s initialize p_n as zero for all other n (i.e., n > 0), and we’ll update these values with each roll. That is, we know these values aren’t really zero, but after some number of operations, they will converge to their correct values.

After the first roll, p₁  remained at 0 (since it was impossible to roll a 1 with two dice), p₂ → 1/36 (I’m using this notation to say that the value of p₂ has been updated to equal 1/36), p₃ → 2/36, p₄ → 3/36, …, and p₁₂ → 1/36. If you ever landed on space 2, you rolled again, at which point you could have landed on any space from 4 to 14. Updating p_n for these spaces meant p₄ → p₄ + p₂ · (1/36), p₅ → p₅ + p₂ · (2/36), p₆ → p₆ + p₂ · (3/36), …, and p₁₄ → p₁₄ + p₂ · (1/36). Each of these updates included a factor of p₂ because the added probabilities were all conditional on you having started from space 2.

Next, if you ever landed on space 3, you rolled again, at which point you could have landed on any space from 5 to 15. Updating p_n for those spaces meant p₅ → p₅ + p₃ · (1/36), p₆ → p₆ + p₃ · (2/36), p₇ → p₇ + p₃ · (3/36), …, and p₁₅ → p₁₅ + p₃ · (1/36).

And so it continued. It was a lot of number-crunching to get the precise answer, and while computer assistance wasn’t technically necessary, it was still helpful.

In the end, p_n peaked when n was 7, meaning space 7 was the most likely to be landed upon. (Hey, that was our initial guess!) Kudos to the numerous solvers who computed the exact probability: p₇ = 1417/6⁵, or about 18.2 percent.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Jason Goldrosen 🎻 from Brooklyn, New York. I received 66 timely submissions, of which 65 were correct—good for a whopping 98 percent solve rate. (And so close to perfection!)

For Extra Credit, you took a closer look at the Oligopoly board, which had 10 spaces on each side. The first side had spaces 0 through 9, the second side had spaces 10 through 19, the third side had spaces 20 through 29, and the fourth side had spaces 30 through 39.

Because you were rolling two dice, it was impossible to land on space 1 in your first pass around the board. Several other spaces on the first side of the board were similarly unlikely.

Which space after the first side (i.e., which space from 10 to 39) were players least likely to land on at some point during their first pass around the board?

The approach outlined above from last week’s Fiddler worked perfectly well here, too. All you had to do was continue computing p_n for larger values of n and look for a minimum.

I’ll be honest—since players were likely to land on space 7, I figured spaces around 14 would be likely as well. After all, rolling back-to-back 7s was fairly likely, with a probability of 1/36. To reach a space like 13 you could roll a 7 and a 6 (or a 6 and a 7), and to reach 15 you could roll a 7 and an 8 (or an 8 and a 7), either of which was similarly fairly likely.

But my intuition proved wrong. Solver 🎬 Angelos Tzelepis 🎬 ran 10 million simulations, finding that (after the first side of the board) space 13 was the least likely to be landed upon. He even made a heatmap version of his own Oligopoly board:

Meanwhile, solvers like Q P Liu computed the exact result: p₁₃ = 22,621,045/(3·6¹⁰), or about 12.5 percent—a result that matched up quite nicely with Angelos’ Monte Carlo methods.

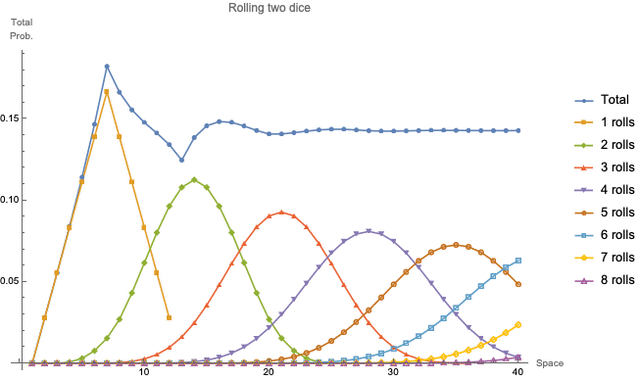
So, why was 13 so unlikely? Solver 🎬 Michael Seifert 🎬 pulled back the curtain a bit by plotting p_n along with the probabilities of landing on each space after different numbers of rolls:

After one roll, you were most likely to land on space 7. And after two rolls, you were most likely to land on space 14. But while space 13 was relatively likely after two rolls, it lay just beyond the possibility of one roll. That made it less likely than 12 and less likely than 14, resulting in a local minimum.

As part of the Extra Credit, I also inquired about the least likely square when three dice were rolled each turn, rather than two dice. Most solvers figured this one out as well, using similar methods. This time, space 17 was least likely to be landed upon.

Finally, for an enlightening read, check out Laurent Lessard’s write-up, in which he uses generating functions to analytically derive a closed expression for p_n, albeit one involving summations, products, and roots of quintic and sextic polynomial equations. (Hey, that’s still super-impressive!)

Laurent even proved that, when rolling k dice, the asymptotic limit of the probability you’d land on any given space after many, many rolls was 2/(7k). Where did the 2 and 7 come from? Well, you might remember from a physics course (like good old quantum mechanics) that the probability of observing a moving object is inversely proportional to its speed at the point of observation. In other words, the faster the object is moving, the less likely you are to observe it. The same goes for Oligopoly. After many, many rolls, your probability of having landed on any given square is the reciprocal of your average speed (i.e., roll), which is 3.5 (the average value of one die) times k (the number of dice). Sure enough, the reciprocal of 3.5k is 2/(7k), the exact limit proven by Laurent.

Hooray for math! Hooray for physics!

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.