Did xkcd Get Its Math Right?

The popular webcomic recently made a joke involving combinatorial mathematics. But did the math actually check out? For Extra Credit, can you find other ways the joke could have been delivered?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

From Seth Cohen comes a comical conundrum:

Seth recently saw the following xkcd webcomic by Randall Munroe:

The question is, very simply: Is this comic mathematically correct?

In other words, let p represent the probability that if you randomly select two arrows from a group of 10 (five of which are cursed), neither arrow is cursed. And let q represent the probability that if you roll three d6 dice (cubes with faces numbered 1 through 6) and one d4 die (a tetrahedron with faces numbered 1 through 4), the sum of the rolls is at least 16.

Does p equal q? If so, determine their common value. If not, determine the value of each.

This Week’s Extra Credit

From Seth Cohen also comes some Extra Credit:

A typical set of dice from Dungeons & Dragons (D&D) includes a d4, a d6, a d8, a d10, a d12, and d20. Here, “dN” indicates a die with N faces numbered 1 through N that are all equally likely to come up.

Again, let p represent the probability that if you randomly select two arrows from a group of 10 (five of which are cursed), neither arrow is cursed.

You want to simulate this event by rolling up to four D&D dice and having the sum be at least some specific value. These dice can all be different from each other, they can all be the same kind of die (say, d4), or anywhere in between, with a few that are the same and others that are different.

How many ways can you simulate picking the arrows, an event with probability p? And what are these ways? (For each way, you should specify the dice as well as the value their sum should be greater than or equal to.)

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a question from one of James Tanton’s puzzle strings, which I’ll paraphrase here:

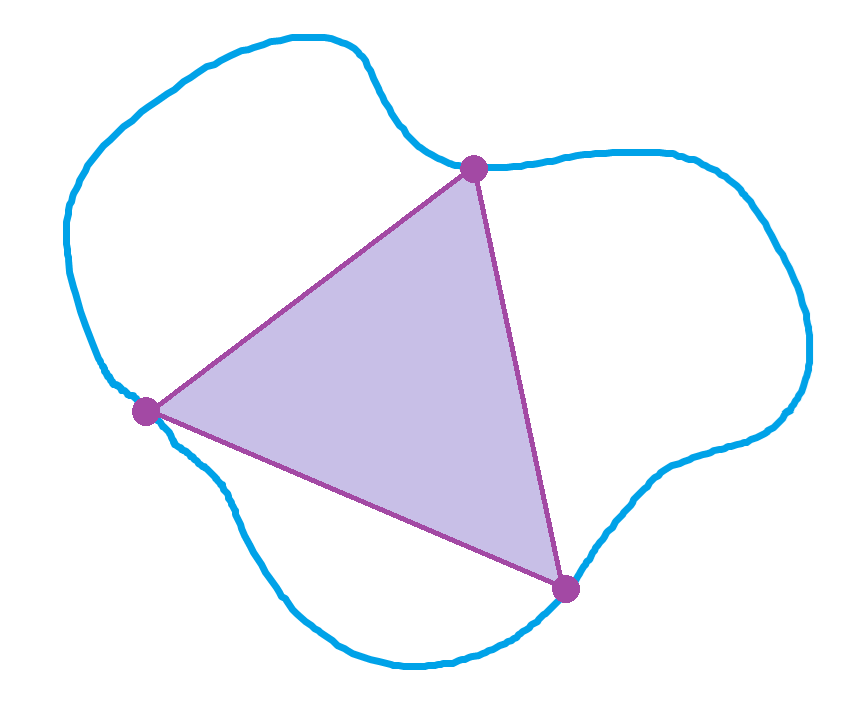
Suppose you have a smooth, closed planar curve, like the one shown below. Is it always possible to find three points on the curve that are the vertices of an equilateral triangle?

As always, feel free to discuss this puzzle and your approach in the comments below.

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Jim 🎻 from Cambridge (although Jim didn’t specify which one). I received 24 timely submissions, of which 16 were correct—good for a 67 percent solve rate.

Last week, you were presented with a regular hexagon with dotted lines extending from the center to each corner. The sections of the hexagon were labeled 0 to 5 in counterclockwise order. Your goal was to fold up the hexagon into a triangular packet the size of one of its sections.

There were, of course, some rules:

• You could only fold along the dotted lines.

• No cutting or tearing was allowed—the hexagon had to remain intact at all times.

• The final packet had to be flat, with the “0” section on top in its original orientation and all the other sections folded behind it.

Using these rules, how many distinct folded-up packets could you generate?

There were three ways you could have folded the hexagon in half (giving you an isosceles trapezoid), and for each of these ways you wanted the half that contained the “0” to remain in front. From there, you always had two different ways to complete the folding.

In particular, if the “0” was in the center of your isosceles trapezoid (i.e., the half-hexagon), then you could fold either the “5” behind it first and then the “1,” or you could fold the “1” behind it first and then the “5.” And if the “0” was on one side of your isosceles trapezoid, you could fold in either direction along the dotted line between the two other visible numbers before tucking everything behind the “0.”

That gave you a total of six distinct packets. Surely, the answer was six, right? Well, 29 percent of readers thought so.

But not so fast! So far, we listed all the ways to generate packets by initially folding the hexagon in half. But you could also have initially folded it into thirds. There were two ways to do this, as shown below:

For each of these, there was only one way to complete the folding into the packet. In total, there were eight distinct packets you could have made.

Several solvers further specified the order in which the resulting numbers appeared on a cross-section through the folded packet. These eight possibilities were, courtesy of solver Nick Carlton:

• 012345

• 012543

• 014325

• 032145

• 034521

• 052341

• 054123

• 054321

At first glance, there didn’t appear to be much of a pattern to these sequences, other than the fact that they all started with zero (as constrained by the problem) and we’ve listed them here in numerical order. As it turned out, there was a pattern—but we’ll save that for the Extra Credit.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Izumihara Ryoma 🎻 from Toyooka, Japan. I received 13 timely submissions, of which only 4 were correct—good for a 31 percent solve rate. This was a really tough one!

Applying the same set of rules as in last week’s Fiddler, how many distinct packets could you have made by folding up a regular octagon?