Can You Fold the Hexagon?

The six sections of a regular hexagon are labeled “0” to “5.” How many distinct ways can you fold up the hexagon so section “0” winds up on top?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

From Tom Keith comes a hexagonal head-scratcher:

Here is a regular hexagon with dotted lines extending from the center to each corner. The sections of the hexagon are labeled 0 to 5 in counterclockwise order. Your goal is to fold up the hexagon into a triangular packet the size of one of its sections.

There are, of course, some rules:

• You can only fold along the dotted lines.

• No cutting or tearing is allowed—the hexagon must remain intact at all times.

• The final packet must be flat, with the “0” section on top in its original orientation and all the other sections folded behind it.

Using these rules, how many distinct folded-up packets can you generate?

This Week’s Extra Credit

From Tom Keith also comes some Extra Credit:

Applying the same set of rules, how many distinct packets can you make by folding up a regular octagon?

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a problem from Frank Morgan, which was sent my way by Jason Zimba. Here’s the spoiler-free statement:

Where should you place two points in a unit square to minimize the average distance in the square to the nearer of the two points? (What about more than two points?)

As always, feel free to discuss this puzzle and your approach in the comments below.

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Chris Vicevich 🎻 from Hamden, Connecticut. I received 24 timely submissions, of which 21 were correct—good for an 87.5 percent solve rate.

Last week’s puzzle concerned Magna-Tiles. They always seem to stick together, regardless of how they are rotated—a property I wouldn’t typically associate with magnets. Put one square tile on top of another and they stick together very well. Rotate one of the squares 90 degrees, they still stick. Flip one over, they still stick. The tiles even stick together (though not as strongly) when placed side by side. Again, rotating or flipping a tile results in the same attraction.

Clearly, the eight magnets embedded along each square’s perimeter must be very cleverly oriented.

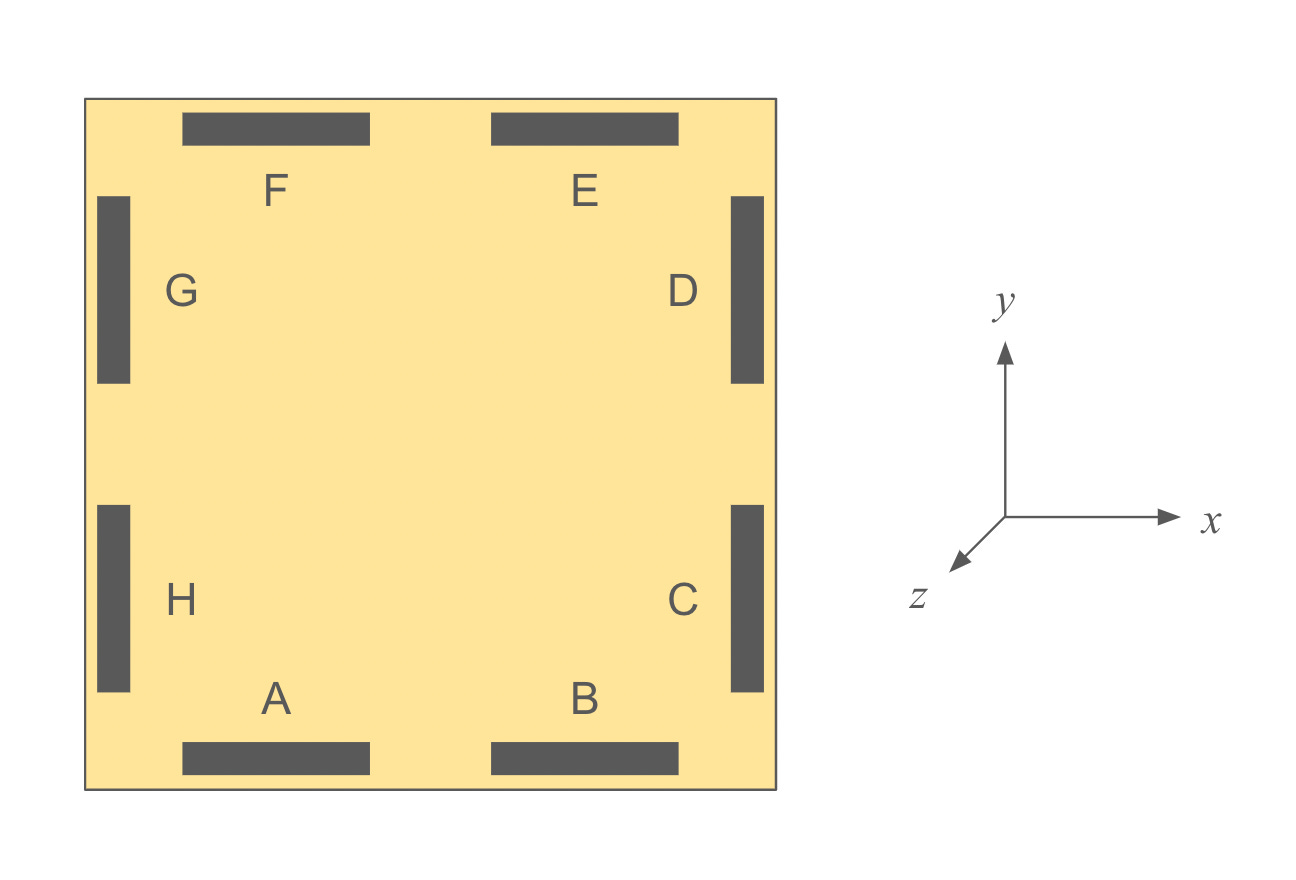
You were asked to consider the following diagram, which showed eight magnets along a square tile’s perimeter, labeled A through H in a counterclockwise manner. The tile lay in the x-y plane, and the z-axis was coming out of the screen toward you.

Given the square tiles’ imperviousness to rotation, what did the orientation of these eight magnets have to be? That is, for each magnet, what was the direction from its south pole to its north pole?

Most bar magnets I’ve seen have poles at either far end, so that the direction from one pole to the other runs along the length of the bar. With this sort of orientation, Magna-Tiles would stick very nicely side-by-side, with the north poles on one tile adjacent to the south poles on the neighboring tile, as shown below. But if you flipped one of these over, they would have repelled each other, since neighboring north poles were now close together, as were neighboring south poles.

You ran into similar issues if you tried to stack one square atop the other. In one case (flip one of the tiles), they attracted each other. But without either tile being flipped, they repelled, as shown below, due to the respective alignments of the north and south poles.

As it turned out, the magnetic vectors didn’t lie in the x-y plane at all. The only way to explain the behavior of Magna-Tiles was if the vectors all pointed in the z-direction, alternating up and down with every magnet around the perimeter.

Solver 🎬 Sophia Wood 🎬 created an awesome animation of 25 rotating Magna-Tile squares, with blue and red representing north and south poles, respectively.

No matter how these Magna-Tiles were rotated, they always attracted each other when laid atop or next to each other. If you’re still not convinced, take a magnet whose poles you know, and place it near a Magna-Tile. Each pole will stick to alternating magnets around the perimeter in the z-direction.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Steve Curry 🎻 from Albuquerque, New Mexico. I received 9 timely submissions, of which 6 were correct, good for a 67 percent solve rate.

When you placed one square Magna-Tile perfectly atop another, they stuck together really well. Suppose each square had side length 1 unit and a thickness of 0.1 units.

We could model each tile’s eight magnets as point monopoles that were either “north” or “south.” (Magnetic monopoles don’t exist, but they were a sufficient approximation for this puzzle.) The poles lay on each edge, one- and three-quarters of the way from one end to the other. You were also told that the energy between any two magnetic monopoles was q₁q₂/r, where r was the distance between them, and q_i was +1 for “north” and -1 for “south.”

When one square lay in a plane directly above another (i.e., the planes were parallel and vertically separated by a distance of 0.1), the lowest-energy arrangement was when the top square was directly above the bottom one. Based on the results of last week’s Fiddler, the magnets alternated polarity as you went around the square, as shown below, with red dots representing north poles and blue dots representing south poles (note that these could be swapped without effect). The left shows the bottom tile’s top face, while the right shows the top square’s bottom face—note that the polarities are swapped vis-a-vis the bottom tile, since this is the opposite face.

Stacking one square directly atop another was a stable arrangement, meaning a slight translation or rotation of either square didn’t lower the energy, which happened to be -54.27. (Note: This figure didn’t include any magnetic energy within a square.)

Your Extra Credit challenge was to determine the stable arrangement with the next-lowest energy. Again, you were asked to assume that the monopoles from one square and the other were vertically separated by 0.1, but that the squares were otherwise free to translate or rotate in their respective planes.

What was this next-best arrangement, and what was its corresponding magnetic energy between the squares?