Could You Have Won the Super Bowl?

The new overtime rules sowed confusion. Would you be better off starting on offense or defense?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

As you may have heard, the 2024 edition of the Super Bowl between Kansas City and San Francisco went into overtime. San Francisco won the coin toss, and therefore had the option to begin the overtime on offense or defense. Their coach opted to start on offense. Because of the various overtime rule changes, and because San Francisco ultimately lost the game, this coach has unsurprisingly faced criticism.

And so, this week, it’s your turn to play coach. Football is complicated, so let’s assume a simplified scoring model. (Because this is just a model, our goal here isn’t necessarily to vindicate San Francisco’s coach, but rather to have fun with some of the math involved.)

Every time your team is on offense, suppose there’s a 1-in-3 chance they score a touchdown (which we’ll say is worth a total of 7 points, as we won’t bother with 2-point conversions here), a 1-in-3 chance they score a field goal (worth 3 points), and a 1-in-3 chance they don’t score any points (i.e., they punt or turn the ball over on downs). After any of these three things happens, your team will then be on defense.

Now, here’s how overtime will work: Your team is on offense first. No matter how many points your team does or does not score, the other team then gets a chance at offense. They have the same probabilities of scoring 7, 3, and 0 points. If the game is still tied beyond this point, the teams will continue alternating between offense and defense. Whichever team scores next wins immediately.

Again, your team is on offense first. What is your team’s probability of winning?

Extra Credit

For Extra Credit, let’s add a smidge more complexity to our model.

If your team happens to score a touchdown on its first possession, then it doesn’t make sense for your opponent to then attempt a field goal, since they’d be guaranteed to lose. Instead, they would attempt to score a tying touchdown.

So let’s add the following to our model: When either team is on offense, they now have a choice. They can still opt for a strategy that results in 7 points, 3 points, or 0 points, each with a 1-in-3 chance. Alternatively, they can opt for a more aggressive strategy that results in 7 points or 0 points, each with a 1-in-2 chance.

Your team remains on offense first. Assuming both teams play to maximize their own chances of Super Bowl victory, now what is your team’s probability of winning?

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a custom-made cryptarithm for readers of The Fiddler, courtesy of Ben Tupper and his wife (also known as “auf & tup”). If cryptarithms are your thing, then you should also check out their daily puzzle!

I’m sharing a screenshot of the custom-made puzzle, but I imagine it’s much more satisfying to work through the digital version.

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Mike Strong 🎻 from Mechanicsburg, Pennsylvania. I received 48 timely submissions, of which 42 were correct—good for an 87.5 percent solve rate!

Last week, you and a friend had a large deck of cards, all of which were numbered 1, 2, 3, or 4. There were many of each of these numbers in the deck.

You alternated placing down one card at a time in a pile. If, at any point, the sum of the most recently played group of cards equaled the sum of a group of cards that had been played immediately before them, then you and your friend both slapped the pile. Whoever slapped first won the pile.

Here were some sequences of cards that would have been slapped once the last card in the sequence was played:

• 3-2-3-4-1 (because the last two cards had a sum equal to that of the two cards prior)

• 1-2-4-3-3 (because the last one card had a “sum” equal to that of the one card prior)

• 2-3-1-2 (because the last two cards had a sum equal to that of the one card prior)

How many cards were in the longest possible sequence that was never slapped?

Let’s start with smaller cases, where the highest card value was 1, 2, or 3, and see if we can find any patterns.

If all the cards had been numbered 1, then the longest unslapped sequence would simply have been 1, which was one card long. Not much going on there.

If the highest card had been 2, then the longest unslapped sequences would have been 1-2-1 and 2-1-2. This was because cards were never allowed to appear in consecutive positions within the sequence, as these two cards had the same “sum.”

Things got more interesting when the highest card was 3. In addition to having no repeats, you could never have 1-2-3, 2-1-3, 3-1-2, or 3-2-1 appear in the sequence. That meant there were eight possible three-card openings that didn’t get slapped:

• 1-2-1. No matter what, the next card would have been slapped.

• 1-3-1. No matter what, the next card would have been slapped.

• 1-3-2. To avoid slapping, the next card had to be a 3.

• 2-1-2. No matter what, the next card would have been slapped.

• 2-3-1. To avoid slapping, the next card had to be a 3.

• 2-3-2. No matter what, the next card would have been slapped.

• 3-1-3. To avoid slapping, the next card had to be a 2.

• 3-2-3. To avoid slapping, the next card had to be a 1.

As noted above, four of the eight openings led to a possible fourth card. Playing these out led to the four following sequences:

• 1-3-2-3-1-3-2. No matter what, the next card would have been slapped.

• 2-3-1-3-2-3-1. No matter what, the next card would have been slapped.

• 3-1-3-2-3-1-3. No matter what, the next card would have been slapped.

• 3-2-3-1-3-2-3. No matter what, the next card would have been slapped.

So when the highest card was 3, the longest unslapped sequences contained seven cards. In retrospect, this probably should have been last week’s puzzle, rather than my upping the ante to a highest card of 4. The leap to 4 moved this puzzle just beyond the point of being reasonable to solve by hand, in my opinion. My bad.

But before moving on to 4, what can we take away from 2 and 3, if anything? For one thing, the longest sequences always had an odd number of cards. Why was that? Because they were each composed of a shorter sequence of cards that was duplicated, with one card separating them in between. For example, the first seven-card sequence above consisted of two subsequences that were both 1-3-2, separated by a 3 in the middle. Perhaps these were patterns that would continue when the highest card was 4?

A few readers hypothesized that there was another pattern. When the highest card was 1, the longest sequence had one card. When the highest card was 2, the longest sequence had one card twice, on either side of a card in the middle, for a total of three cards. When the highest card was 3 the longest sequence had three cards twice, on either side of a card in the middle, for a total of seven cards. In other words, when the highest card N, the longest sequence had length 2^N−1, when N was 1, 2, or 3. This pattern predicted that when N was 4, the longest sequence would have 15 cards—two subsequences of seven cards on either side of a card in the middle.

As I already said, finding the longest sequence when the highest card was 4 was no walk in the park to solve by hand. You could continue in the fashion by which we just analyzed when the highest card was 3—eliminating possible sequences whenever no next card could be placed, and continuing to build upon the sequences that remained. Alternatively, many solvers wrote computer code to do exactly this, albeit faster and (ideally) error-free.

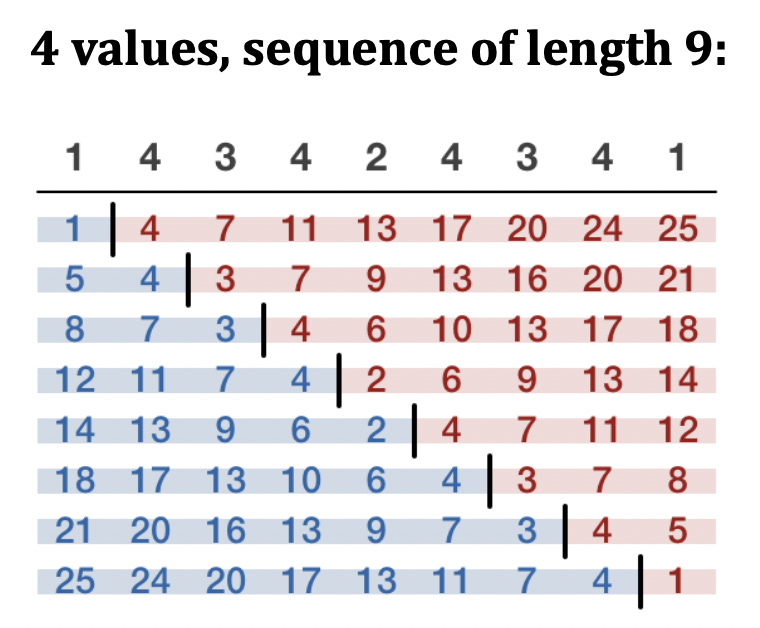
In the end, there was a unique longest sequence, and it was not 15 cards long. It was just nine cards long, and that unique sequence was 1-4-3-4-2-4-3-4-1. Interestingly, this sequence was a palindrome, and did not contain two identical subsequences on either side of a middle card.

Solver 🎬 Tom Keith 🎬 demonstrated that this sequence was unslappable with a nifty table:

The top row shows the values of the cards in the sequence. Each row below the top one considers a different partition point between the sums. If, at any point, the sum before the partition equals the sum after the partition, the sequence would have been slapped. Since the values in each row are unique to that row, this sequence is indeed unslappable.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 David Slater 🎻 from Okemos, Michigan. I received 35 timely submissions, of which 33 were correct—good for a whopping 94 percent solve rate!

For Extra Credit, instead of having cards numbered 1 through 4, they were numbered 1 through N.

When N was 5, how many cards were in the longest possible sequence that was never slapped? What if N was 6? What if N was 7?