Can You Sum Some Cards?

Using the numbers 1, 2, 3, and 4, how long of a sequence can you make without any adjacent groups of numbers having the same sum?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

My friend and I play card games that often result in some very interesting mathematical conversations. One such conversation turned into a puzzle a few weeks back, and it was only a matter of time before it happened again:

You and a friend have a large deck of cards, all of which are numbered 1, 2, 3, or 4. There are many of each of these numbers in the deck.

You alternate placing down one card at a time in a pile. If, at any point, the sum of the most recently played group of cards equals the sum of a group of cards played immediately before them, then you and your friend both slap the pile. Whoever slaps first wins the pile.

Here are some sequences of cards that would be slapped once the last card in the sequence is played:

• 3, 2, 3, 4, 1 (because the last two cards have a sum equal to that of the two cards prior)

• 1, 2, 4, 3, 3 (because the last one card has a “sum” equal to that of the one card prior)

• 2, 3, 1, 2 (because the last two cards have a sum equal to that of the one card prior)

How many cards are in the longest possible sequence that is never slapped?

By the way, if you’re someone who’s just dying to see a Fiddler in more concise (and precise) mathematical language, then you’re in luck this week! Here’s the very same puzzle, but without that bothersome card game:

Determine the maximum k for which there exists a sequence a₁, a₂, ..., a_k ∈ {1, 2, 3, 4}, such that for all values p, q, r with 1 ≤ p ≤ q < r ≤ k it is never true that

\(\sum_{m=p}^{q}{a_m} = \sum_{n=q+1}^{r}{a_n}.\)

Extra Credit

In the preceding puzzle, the numbers on the cards were 1 through 4. Suppose, instead, they were numbered 1 through N.

When N is 5, how many cards are in the longest possible sequence that is never slapped? What if N is 6? What if N is 7?

Making the Rounds

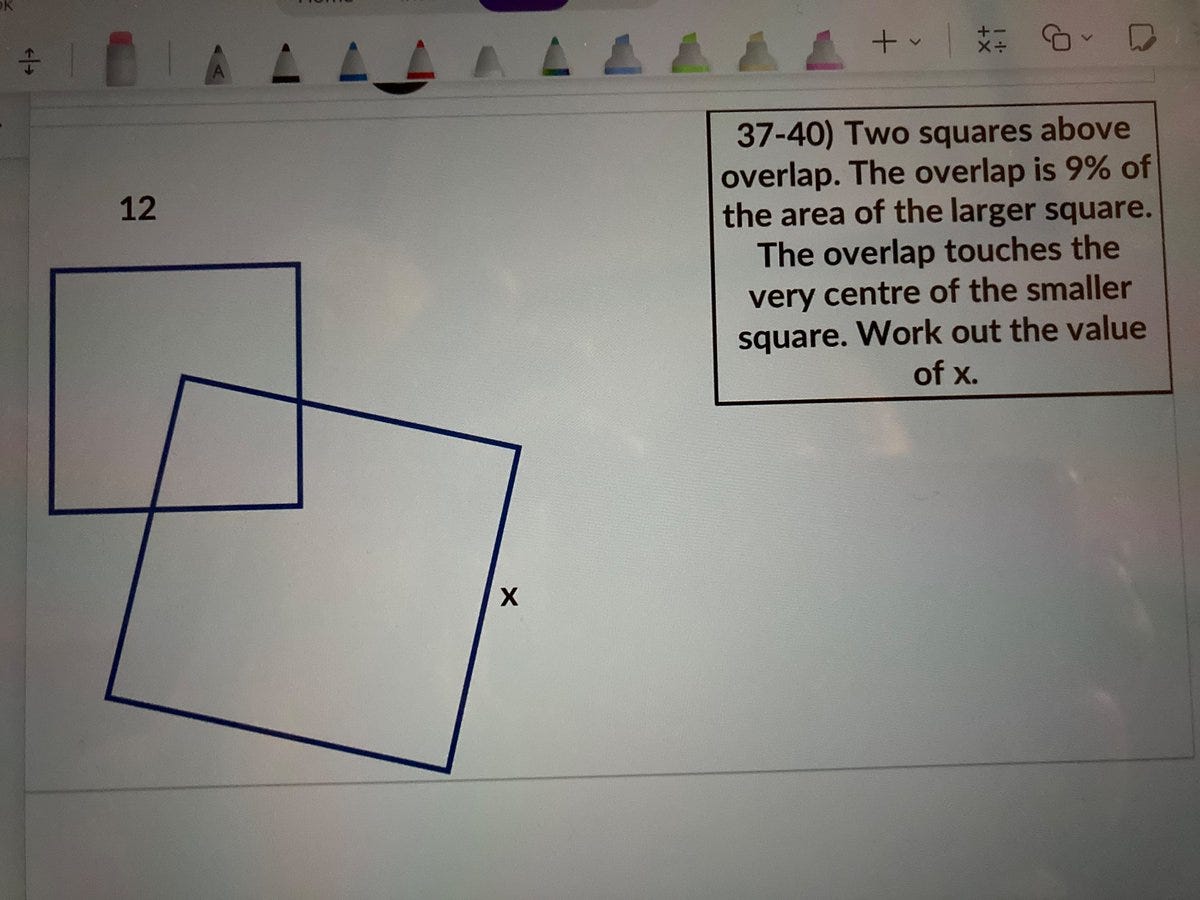
There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a geometry nugget that was apparently assigned to the daughter of Fields Medal recipient Timothy Gowers. For a spoiler-free experience, here’s an image of the problem:

To be clear, 12 is the side length of the smaller square and x is the side length of the larger square. For an extra challenge, see if you can solve this entirely in your head!

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Benjamin Phillabaum 🎻 from Lafayette, Indiana. I received 29 timely submissions, of which 14 were correct—good for a 48 percent solve rate. As Fiddlers go, this was a tough one, especially if you were working by hand.

Last week, Nikoli the snake wanted to slither along a loop through a 4-by-4 grid of points. To form a loop, Nikoli could connect any horizontally or vertically adjacent points with a line segment. However, Nikoli had certain standards when it came to loop construction. In particular:

• The loop could never cross over itself.

• No two corners of the loop could meet at the same point.

• Once Nikoli had crossed the connection between two points, Nikoli couldn’t cross it again (in either direction).

For example, the following two constructions were valid loops:

Meanwhile, the following three constructions were not valid. The one on the left crossed over itself, the one in the middle had two corners that met at a single point, and the one on the right required Nikoli to pass over the same line segment twice.

How many unique loops could Nikoli make on the 4-by-4 grid? (For any given loop, Nikoli could travel in two directions around it. However, these should still have been counted as a single loop.)

Instead of thinking about the loop itself, a popular strategy was to look at the space inside the loop. More specifically, as noted by solver Dan Katz, that shape had to be a polyomino that fit on the grid. You could tackle these cases based on the size of the polyomino:

• There was only one kind of monomino: a tiny square. It had nine possible locations on the grid. Altogether, there were nine loops around monominoes.

• There was one kind of domino. Accounting for translations and rotations, there were 12 loops around dominoes.

• There were two kinds of trominoes: straight and L-shaped. Accounting for translations and rotations, there were 22 loops around trominoes.

• There were five kinds of tetrominoes: straight (which didn’t fit), square, T-shaped, L-shaped, and skew. Accounting for translations, rotations, and reflections, there were 36 loops around tetrominoes.

• Of the 12 kinds of pentominoes, only eight of them could fit within the grid, Altogether, there were 49 loops around pentominoes.

• Of the 35 kinds of hexominoes, again only eight of them could fit within the grid. Altogether, there were 48 loops around hexominoes.

• Of the 108 kinds of heptominoes …

You know, at some point, it was easier to construct loops based on which squares were missing from the interior rather than which squares were included. Since a heptomino was made of seven squares, that meant two of the nine had to be missing. If one of these was the center, the other had to be adjacent to it, giving four possible loops. Otherwise, any two of the eight non-center squares could be missing, giving 8 choose 2 (or 28) loops—provided the two missing squares didn’t cut off a corner square from the rest (one of the red counterexamples shown above). Altogether, there were 28 loops around heptominoes.

Forget how many octominoes there are. (Okay, there are 369.) With eight squares in the loop, the one missing square could have been any of the nine except the middle. That meant there were eight loops around octominoes.

Finally, there was just one loop around a nonomino (an awesome word, by the way). That was when all nine squares were inside the loop.

Adding up all these polyomino cases gave the total number of loops, which was 9 + 12 + 22 + 36 + 49 + 48 + 28 + 8 + 1, or 213.

Several solvers, including 🎬 Michael Schubmehl 🎬 and 🎬 Tom Keith 🎬, went the extra mile by plotting all 213 of these loops (with some computer assistance). In particular, Michael plotted all 2⁹ (or 512) ways to select a group among the nine squares, and then colored the 213 selections that resulted in a successful loop:

As per usual, a couple of solvers (this time around, it was Mike Strong and Dennis Okon) observed that there was an OEIS sequence that gave away the answer to the puzzle. According to this sequence, there was 1 loop around what I had defined as a 2-by-2 grid, 13 loops around what I had defined as a 3-by-3 grid, 213 loops around what I had defined as a 4-by-4 grid, and 9,349 loops around what I had defined as a 5-by-5 grid. Judging by how quickly this sequence grew, I think it was pretty clear why the 4-by-4 grid was chosen for the puzzle.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Sanandan Swaminathan 🎻 from San Jose, California. I received 9 timely submissions, of which 8 were correct—good for an 89 percent solve rate. That wasn’t a whole lot of solvers, which meant every one of them got a shoutout below!

In a Slitherlink, you connect adjacent points in a grid to form a loop that does not self-intersect, as described above. But what makes a Slitherlink a puzzle is that numbers are provided in some of the spaces between four grid points. These numbers specify how many of the four surrounding edges are present in the desired loop. Then it’s entirely up to you to draw the loop.

As an example, last week I offered a puzzle I had encountered on a Slitherlink site, as well as its solution. (I marked red x’s where I knew there couldn’t be any edges—a helpful strategy when solving such puzzles.)

For Extra Credit, I wanted to know how many distinct Slitherlink puzzles you could create on a 4-by-4 grid of points. Each puzzle consisted of a placement of numbers (from 0 to 4) between grid points, and had to result in exactly one loop. Note that multiple distinct puzzles could result in the same loop, but again, each puzzle itself could have only one loop solution.

Note: What I called a “4-by-4” grid was technically a “3-by-3” Slitherlink, since the latter described the array for the numbers, rather than the points. But to keep things consistent between the puzzles last week, I steadfastly called this a “4-by-4” grid.