Can You Win the Collaborative Card Game?

You and a friend each shuffle your own deck of cards. If you both flip cards over one at a time, how often will you never see matching cards?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

This week’s puzzle is based on a suggestion from Stephen Cranston. Some of you may no doubt be familiar with this one, but it was new to me (I think?), and it was so juicy that I just had to share it.

You and a friend each have a standard deck with 52 cards. You thoroughly shuffle your deck, while your friend thoroughly shuffles theirs. Then, you both draw cards one at a time. If the first card you draw is the same as the first card your friend draws, you lose! Otherwise, you draw again. If the next card you draw is the same as the next card your friend draws, you lose! Otherwise … and so on.

If the two of you can make it through your entire decks without ever drawing the same card at the same time, you both win. Otherwise, you both lose.

What is the probability that you and your friend will win this collaborative game?

Extra Credit

If you’ve already seen some version of this week’s Fiddler before, then you should try your hand at this variant:

Once again, you and your friend both have standard decks of 52 cards. This time, you first combine them into a single deck with 104 cards, and you thoroughly shuffle it. Then, you randomly split this back into two decks with 52 cards each—one for you, and one for your friend.

At this point, you continue as before, with each of you drawing one card at a time. If the two of you can make it through your entire decks without ever drawing the same card at the same time, you both win. Otherwise, you both lose.

What is the probability that you and your friend will win this collaborative game?

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a question about one of the “einstein” monotiles that caught my attention.

Here’s part of a figure from the 2023 paper, “​​An aperiodic monotile”:

The tiles in dark blue are reflections of the other tiles. As the number of tiles increases (toward infinity), what fraction of the tiles will be dark blue?

I’m not sure if this question was posted as a joke, due to the tiling’s aperiodic nature. But thanks to the substitution methods from the original paper, this question might be answerable…

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Emilie Mitchell 🎻 from Nashville, Tennessee. I received 26 timely submissions, of which 22 were correct—good for a 85 percent solve rate.

Last week’s puzzle was inspired by the eclipse. But instead of covering a circle (i.e., the Sun) with another circle (i.e., the Moon), you wanted to cover a circle with ellipses. (I mean, how cool would it be to have a moon shaped like Haumea?)

More specifically, you wanted to cover a unit circle (i.e., a circle with radius 1) using two congruent ellipses. These ellipses could have had any eccentricity you liked, but they had to be congruent to each other.

What was the smallest possible area one of these ellipses could have had, such that they completely covered the circle?

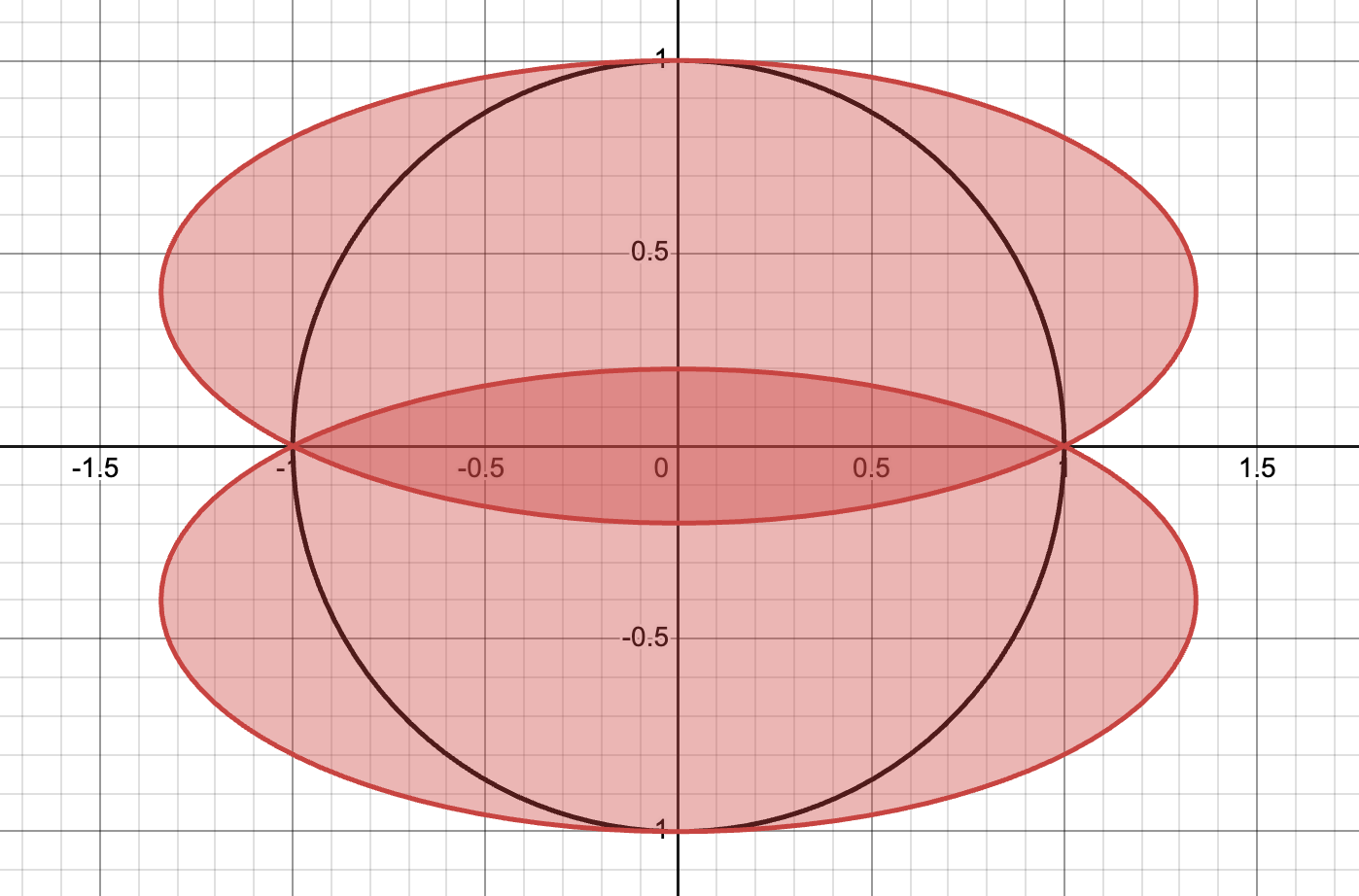
The approach most solvers took was to have two ellipses stretched across the two halves of the circle, as shown below. This resulted in some overlap of the ellipses, but so be it—some overlap was inevitable.

In the image above, the upper ellipse passed through the points (1, 0), (-1, 0), and (0,1); the lower ellipse was a reflection across the x-axis, so it passed through the points (1, 0), (-1, 0), and (0, -1). If you could find an equation for one of these ellipses, then perhaps you could somehow use it to minimize that ellipse’s area.

The general formula for an ellipse oriented along the x- and y-axes is (x−h)²/a² + (y−k)²/b² = 1, where (h, k) is the center of the ellipse, and a and b are the lengths of the semi-major and semi-minor axes (not necessarily respectively). The area of such an ellipse is 𝜋ab, a fact we’ll need later on when minimizing the area.

The upper ellipse was centered on the y-axis, which meant h was zero for this ellipse. Its equation was therefore x²/a² + (y−k)²/b² = 1, which had three unknowns: a, b, and k. As we already said, you also knew it had to pass through three points: (1, 0), (-1, 0), and (0,1). However, this was not enough information to identify a single ellipse, since passing through (1, 0) automatically meant it also passed through (-1, 0).

In short, you wanted to find an ellipse of the form x²/a² + (y−k)²/b² = 1 that had solutions (1, 0) and (0, 1). Plugging in (1, 0) for (x, y) gave you the equation 1/a² + k²/b² = 1. Meanwhile, plugging in (0, 1) for (x, y) gave you the equation (1−k)²/b² = 1.

With three variables and two equations, the best you could do was find a family of ellipses in terms of a single variable—k was a good a choice as any, meaning we’ll express a and b in terms of k.

The second equation above told you that b = 1−k. Plugging that result into the first equation gave you a = (1−k)/√(1−2k). By trying out different values of k between 0 and 0.5, you could find all sorts of pairs of congruent ellipses (with corresponding values of a and b) that completely covered the circle. The animation below shows these ellipses, which varied from circles (when k was zero) to strips of infinite eccentricity (when k was 0.5).

But which ellipses had the least area? Earlier, we said the area of an ellipse is 𝜋ab, which meant the upper (and lower) ellipse’s area in terms of k was 𝜋(1−k)²/√(1−2k). To find the minimum of this function, you could take the derivative with respect to k and set it equal to zero. If, like me, you’re not a fan of square roots, you could also have minimized the square of this function, as the same value of k minimized both the area and the square of the area.

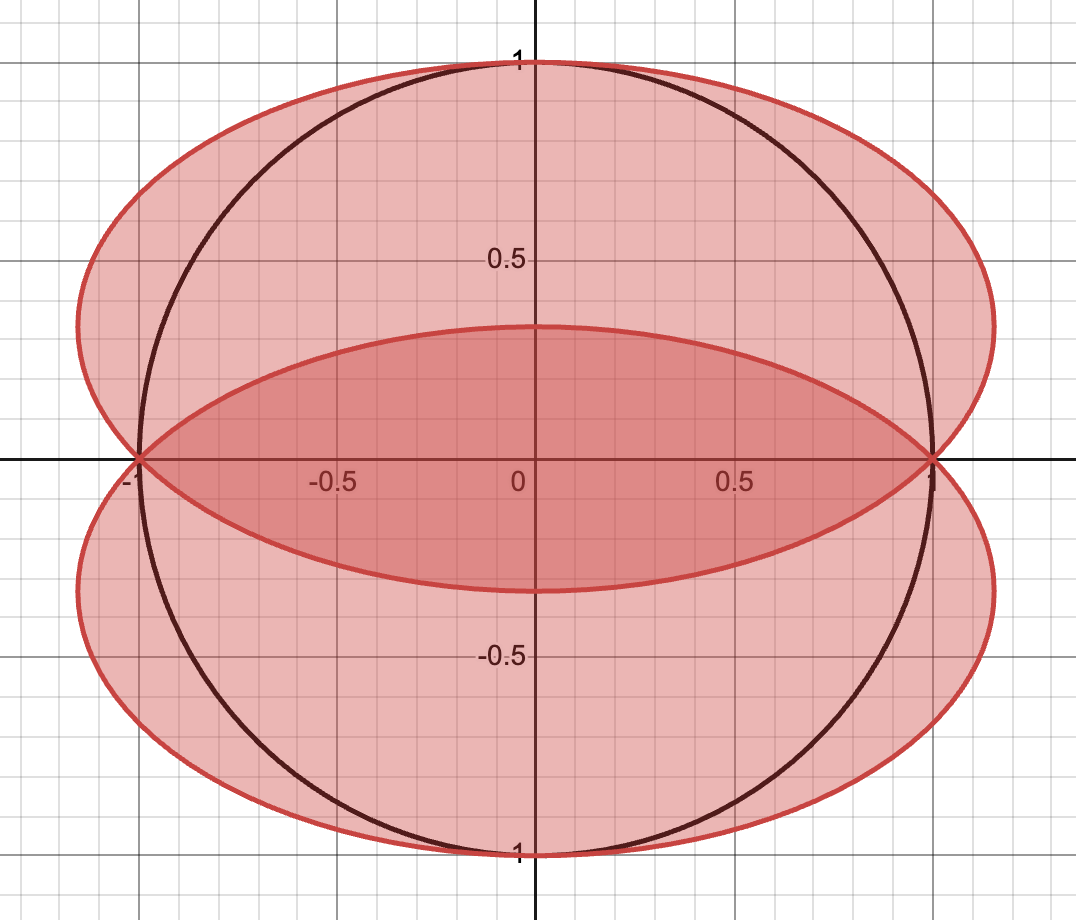
So what value of k minimized (1−k)⁴/(1−2k)? (Yes, we discarded the constant coefficient of 𝜋² here.) By the quotient rule, the derivative was a fraction whose numerator was 2(1−k)⁴ − 4(1−k)³(1−2k). Setting this equal to zero and dividing through by 2(1−k)³ gave you (1−k) − 2(1−2k) = 0, the solution to which was k = 1/3. After all that work, it turned out the ellipses were centered at the suspiciously friendly-looking coordinates (0, 1/3) and (0, -1/3), as shown below.

As for each ellipse’s area, having k = 1/3 meant 𝜋(1−k)²/√(1−2k) was equal to 4𝝅√3/9, or approximately 2.4184. In other words, each ellipse itself had approximately 77 percent of the circle's area. If you happened to double this answer, giving me the combined area of the two ellipses, I still marked you as correct.

By the way, solver Tom Singer found the rather intriguing result that the foci of these two ellipses just happened to be on the circumference of the circle as well. Weird, right?

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Eric Widdison 🎻 from Kaysville, Utah. I received 14 timely submissions, of which 11 were correct—good for a 79 percent solve rate.

Instead of two congruent ellipses, now you were asked to cover the unit circle with three congruent ellipses. What was the smallest possible area one of these ellipses could have had, such that they completely covered the circle?