Can You Eclipse via Ellipse?

Suppose you want to cover a circle with two congruent ellipses. How small can those ellipses be?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

Like many folks around the United States and Mexico, I had the chance to see a mostly-occluded sun this past Monday. (It’s pretty remarkable that the sun and the moon have such similar apparent sizes in the sky.)

But instead of one circular shape obscuring another, what if there were two such shapes? In other words, suppose you have two congruent circles that, together, completely cover another circle. How small could those two congruent circles be?

The answer to this version of the “disk covering problem” turns out to be rather boring: Both circles must be the same size as the one they cover. In the past, when circles have proven uninteresting for one reason or another, I turn to ellipses. (How cool would it be to have a moon shaped like Haumea?)

So suppose you have two congruent ellipses that, together, cover a unit circle (i.e., a circle with radius 1). These ellipses can have any eccentricity you like, but they must be congruent to each other.

What is the smallest possible area one of these ellipses can have, such that they completely cover the circle?

Extra Credit

(You probably know what’s coming…)

Instead of two ellipses, suppose you are trying to cover the unit circle with three congruent ellipses. What is the smallest possible area one of these ellipses can have, such that they completely cover the circle? (If you are so inclined, then by all means look for N congruent ellipses, with N > 2.)

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. While the AI Math Olympiad hasn’t seemed to progress much in recent days (as of the time of this writing, the top score remains 17 out of 50), I’m sharing an intriguing question I recently saw on social media, which I’ll attempt to paraphrase:

Alice has n positive real numbers, which we’ll call a₁, a₂, …, a_n, such that the sum of these numbers is n. Alice informs her friend Bob that either all n numbers are the same (meaning they’re all equal to 1), or their mean absolute deviation (i.e., the average difference between each number and the mean, which is 1) is greater than 0.1.

Bob is trying to figure out whether or not all the numbers are equal. To find out, he can ask Alice to reveal one of the n numbers at random, such that the probability of picking the number a_k is proportional to a_k (meaning the probability is a_k/n), or he can ask Alice to draw two specific indices p and q and find out if a_p > a_q.

How many questions does Bob need to figure this out? More specifically, does this number of questions scale with n, does it scale with the square root of n, or does it remain constant as n increases?

So either every number is 1, or some fraction of them must differ from 1 by a collective amount (while maintaining an average of 1). It seems to me the key is how many questions Bob needs until he can pin down a value that’s not 1, which doesn’t seem like it would take too many questions—at least, not on average. But I’m wondering if this is asking about the average number of questions Bob needs, or the maximum number of questions Bob needs.

So, what do you think the answer is?

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Ed Foley 🎻 from Redmond, Washington. I received 78 timely submissions, of which 73 were correct—good for a 94 percent solve rate.

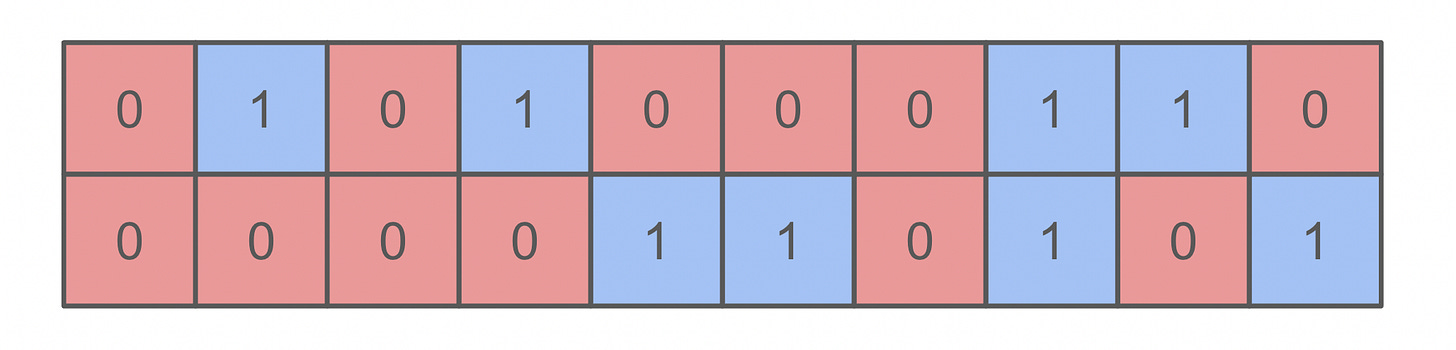
Last week, I was painting an infinitely long strip of canvas that was 1 cm wide. It was broken up into adjacent 1 cm-by-1 cm squares, each of which was independently numbered zero or one, each with a 50 percent chance. Every square with a zero I colored red, while every square with a one I colored blue.

Once I finished painting, there were many “clusters” of contiguous red and blue squares. For example, the finite strip of canvas below contained 10 total squares and seven clusters, which meant the average size of a cluster here was approximately 1.43 cm².

So, once I finished painting the entire, infinite strip, what was the average size of each red or blue cluster?

Solver Chris Payne ran a simulation—not in Python or MATLAB, but in Excel! Chris randomly assigned values of 0 or 1 to 1,000 cells, and then tallied up the average size of the clusters. Thanks to randomization, this average came out to be a different value every time you reloaded the page, but it was typically around 2. Could that have been the answer?

Suppose you were painting the strip from left to right and you encountered a square whose color was different from the previous square’s, meaning this was the start of a new cluster. How long did you expect this cluster to be?

There was a 50 percent chance the next square had a different color, meaning the cluster’s length was 1. There was a 25 percent chance that the cluster’s length was 2, since you needed the next square to be the same color (50 percent) and the square after that to be the other color (50 percent). Continuing in this fashion, there was a 12.5 percent chance the cluster’s length was 3, a 6.25 percent chance the length was 4, and so on.

To find the average length of a cluster, you had to multiply these lengths by their respective probabilities, and then add up all the resulting products. Writing these terms as fractions, you had 1/2 + 2/4 + 3/8 + 4/16 + 5/32 + 6/64 + …, which you could equivalently write using powers of 2 in the denominators: 1/2¹ + 2/2² + 3/2³ + 4/2⁴ + 5/2⁵ + 6/2⁶ + … + N/2^N + ….

This is known as an arithmetic-geometric series, in which the numerators form an arithmetic sequence and the denominators form a geometric sequence. One way to calculate the sum was to break up the terms into unit fractions: (1/2) + (1/2² + 1/2²) + (1/2³ + 1/2³ + 1/2³) + (1/2⁴ + 1/2⁴ + 1/2⁴ + 1/2⁴) + …. Adding the first term from each parenthetical gave 1/2 + 1/2² + 1/2³ + 1/2⁴ + …, a geometric series whose sum was 1. Adding the second term in each parenthetical (if it existed) gave 1/2² + 1/2³ + 1/2⁴ + …, a geometric series whose sum was 1/2. Adding the third terms gave 1/4, while adding the fourth terms gave 1/8. The sum of each such set of terms was half the sum of the previous set.

Summing these geometric series gave 1 + 1/2 + 1/4 + 1/8 + …, itself a geometric series whose sum was 2. Chris’ simulation was spot on: The average size of a cluster was precisely 2 cm².

Another approach—which we’ll return to for last week’s Extra Credit—was to determine the probability that a given square was the start of a new cluster. This happened when that square was a different color from the preceding square, which occurred with probability 1/2. And so, as the number of squares N went to infinity, the expected number of clusters approached (1/2)·N. That meant the average cluster size approached N/[(1/2)·N], or 2 cm², the same answer we just found.

Finally, solver Izumihara Ryoma noted an interesting paradox related to how clusters were sampled. What if, instead of asking for the average cluster size, we asked how large we expected a cluster to be that contained a given square. Before looking at an infinite strip, let’s return to the finite example I provided above:

We already said the average cluster size for this strip was (1+1+1+1+3+2+1)/7, or approximately 1.43 cm². But if you picked one of the 10 squares and averaged its resulting cluster size, you got (1+1+1+1+3+3+3+2+2+1)/10, or 1.8 cm². This value was greater, since each larger cluster had a greater probability of being sampled than any given smaller cluster.

For an infinite strip, once you picked a square to look at, you had an average of 1 cm² of the same cluster to its left, and another 1 cm² of the cluster to its right. That gave you a total of 3 cm², which was indeed greater than the accepted answer of 2 cm².

I thought this was a pretty neat aside. Yes, the average cluster size was 2 cm². But the moment you pointed to any given square, that square’s average cluster size was 3 cm². 🤯

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Austin Shapiro 🎻 from Oakland, California. I received 43 timely submissions, of which 29 were correct—good for a 67 percent solve rate.

Once again, I was painting an infinitely long strip of canvas, broken up into adjacent 1 cm-by-1 cm squares. As before, squares were randomly and independently numbered 0 or 1. But this time, the strip itself was 2 cm wide.

Squares were considered adjacent if they shared a common edge. So squares could be horizontally or vertically adjacent, but not diagonally adjacent.

Once I finished painting, there were again many “clusters” of contiguous red and blue squares. The example below contained 20 total squares and nine clusters, which meant the average size of a cluster here was approximately 2.22 squares.

So, once I finished painting the entire, infinite strip, what was the average size of each red or blue cluster?