Can You Win at “Rock, Paper, Scissors, Lizard, Spock?”

You’re playing a dastardly variant of “Rock, Paper, Scissors.” How often will you win outright?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

From Jake Conway comes a question regarding a variant of a well-known game:

In a game of “Rock, Paper, Scissors,” each element you can throw ties itself, beats one of the other elements, and loses to the remaining element. In particular, Rock beats Scissors beats Paper beats Rock.

“Rock, Paper, Scissors, Lizard, Spock” (popularized via The Big Bang Theory) is similar, but has five elements you can throw instead of the typical three. Each element ties itself, beats another two, and loses to the remaining two. More specifically, Scissors beats Paper beats Rock beats Lizard beats Spock beats Scissors beats Lizard beats Paper beats Spock beats Rock beats Scissors.

Three players are playing “Rock, Paper, Scissors, Lizard, Spock.” At the same time, they all put out their hands, revealing one of the five elements. If they each chose their element randomly and independently, what is the probability that one player is immediately victorious, having defeated the other two?

This Week’s Extra Credit

The rules for “Rock, Paper, Scissors” can concisely be written in one of the following three ways:

• Rock beats Scissors beats Paper beats Rock

• Scissors beats Paper beats Rock beats Scissors

• Paper beats Rock beats Scissors beats Paper

Each description of the rules includes four mentions of elements and three “beats.”

Meanwhile, as previously mentioned, a similarly concise version of the rules for “Rock, Paper, Scissors, Lizard, Spock” (and adapted from the original site) is:

• Scissors beats Paper beats Rock beats Lizard beats Spock beats Scissors beats Lizard beats Paper beats Spock beats Rock beats Scissors

In this case, there are 11 mentions of elements and 10 “beats.” Including the one above, how many such ways are there to concisely describe the rules for “Rock, Paper, Scissors, Lizard, Spock?”

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing the fact that LinkedIn has … games?

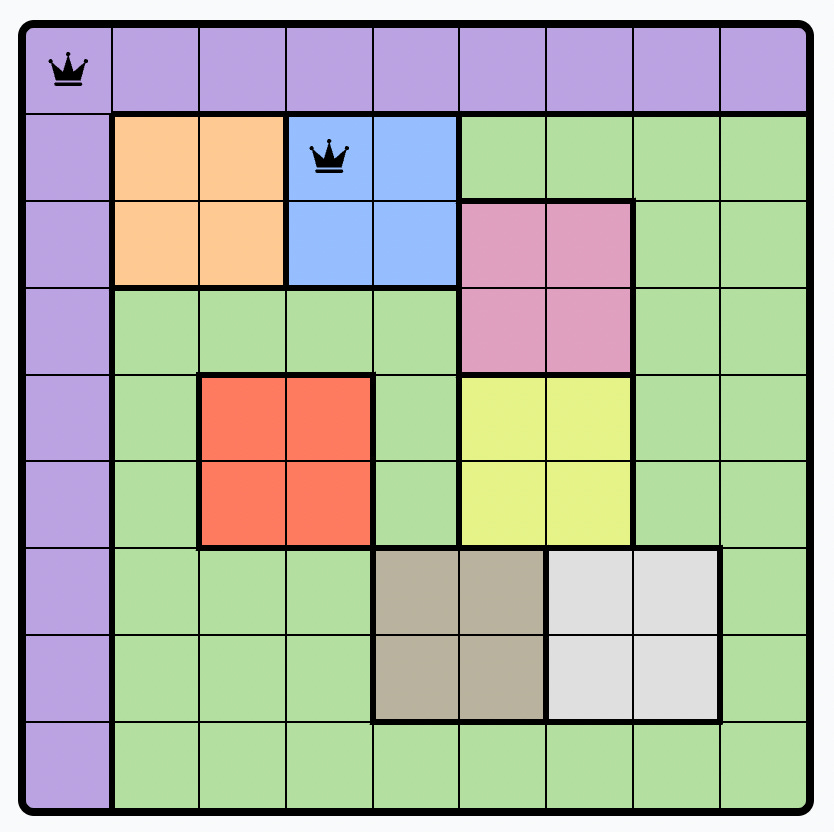
Apparently they do. One of them, Queens, feels like the offspring of chess and sudoku. (It’s essentially Star Battle … with a color scheme?) On a square grid, your goal is to have exactly one queen in each row, column, and color region. Two queens cannot touch each other, not even diagonally.

Here’s a partially filled board I encountered (and, to my credit, ultimately solved):

Check it out, and let me know if their other games are any good!

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Kevin Lin 🎻 from Austin, Texas. I received 49 timely submissions, of which 42 were correct—good for an 86 percent solve rate.

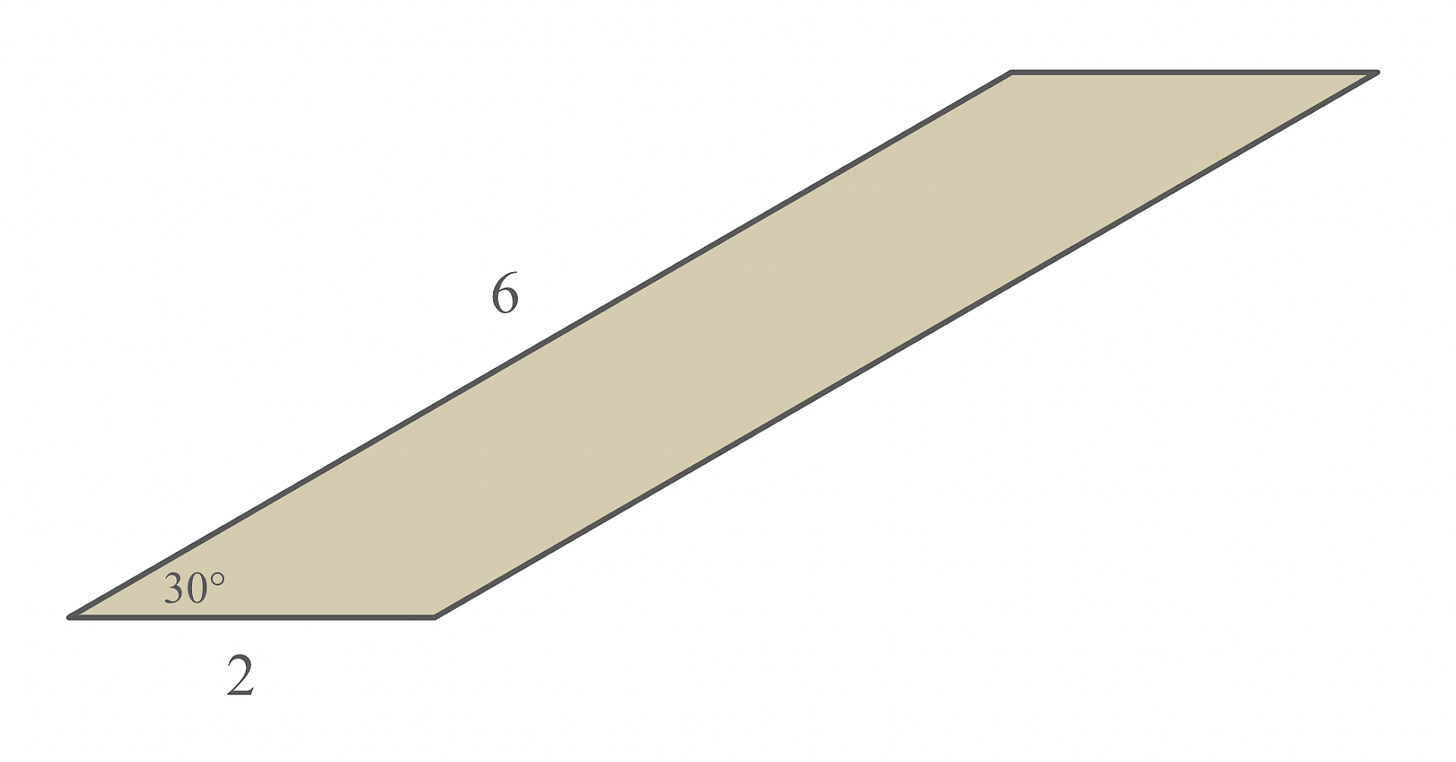
Last week’s puzzle was one worth pondering … on the toilet! You had the parallelogram of cardboard shown below, with side lengths of 2 units and 6 units and angles of 30 degrees and 150 degrees:

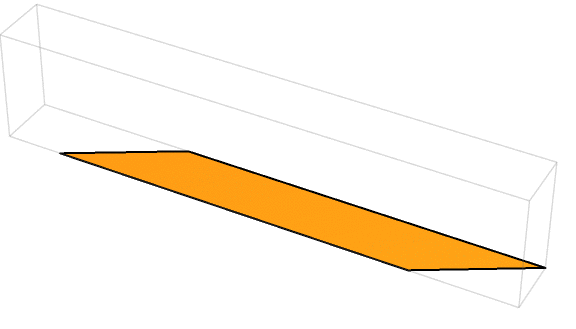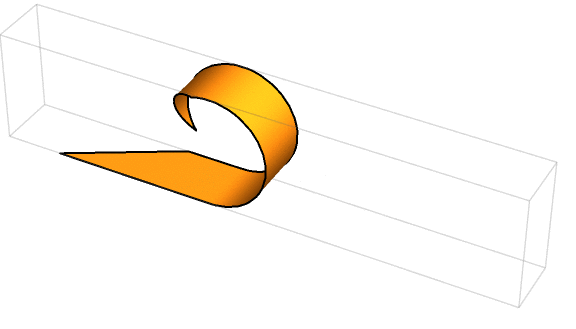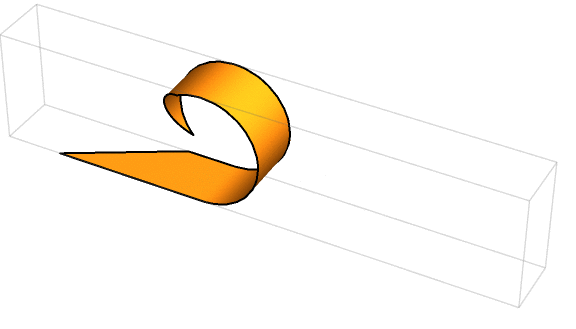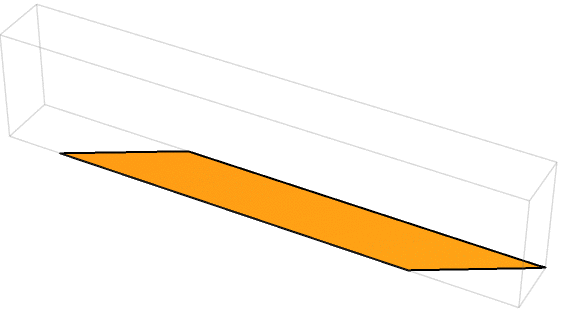
By swirling two edges together, it was possible to neatly (without any overlap) generate the lateral surface of a right cylinder—in other words, a toilet paper roll!

If you weren’t convinced, you could gently tear a toilet paper roll along its diagonal seam and then unwrap it into a flat shape. You got a parallelogram! Solver Peter Ji did exactly this:

Your challenge was to determine the volume of a cylinder you could make from the particular piece of cardboard diagrammed above.

The formula for the volume of a right cylinder is 𝜋r²h, where r is the radius of the circular base and h is the height. So, how could you determine values for r and h for the given parallelogram?

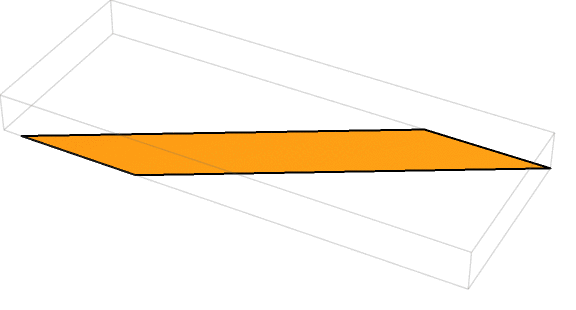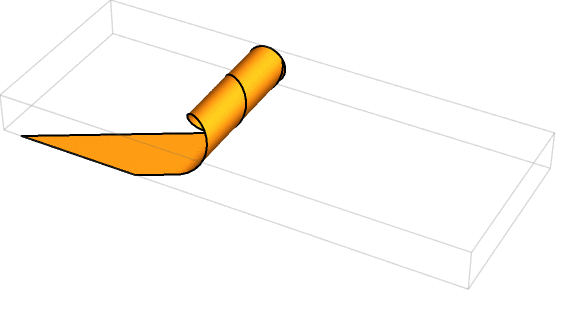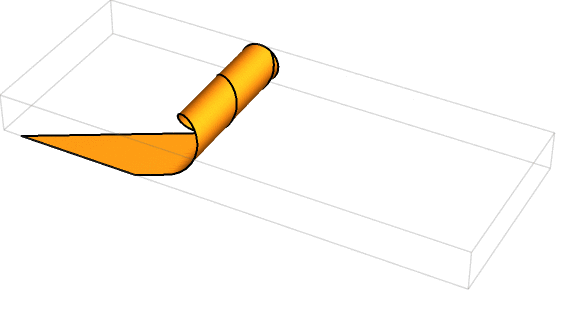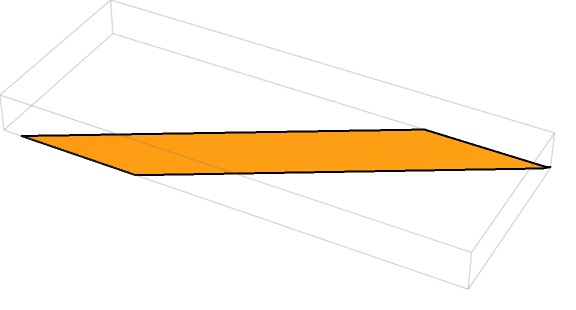
This is the part where I’d normally say that a drawing helps. But given that we’re dealing with furling and unfurling in three dimensions, instead I’ll say that an animation helps. Here was one such looping animation, courtesy of solver 🎬 Michael Schubmehl 🎬:

If you watched this enough times, you’d notice that the short sides of the parallelogram (which had lengths of 2 units) became the circumferences of the circular bases. That meant 2𝜋r = 2, or that r = 1/𝜋 units.

With this radius in hand, all that was left was to determine the cylinder’s height. Based on the animation, that was the height, or altitude, of the parallelogram itself. With a little trigonometry, that came out to be 6·sin(30°), or 3 units. That meant h was 3.

Plugging these values of r and h into the formula for the cylinder’s volume, you got 𝜋r²h = 𝜋·(1/𝜋)²·3 = 3/𝜋 cubic units. That was the volume of the cylinder animated above.

A whole bunch of solvers submitted this perfectly correct answer. But others submitted a different response. Was it possible that there was more than one solution here? Indeed, it was!

To see why, let’s return to the original parallelogram. So far, we’ve been assuming that its two shorter sides would become the circumferences of the two circular bases, while the longer sides met to form a helix that wrapped around the cylinder’s height. That resulted in a cylinder that was taller than it was wide, something we’re accustomed to seeing with paper towel rolls.

But it was equally valid to swap which sides became the circumference versus the helix. That is, you could have the longer sides become the circumferences of the circular bases, while the shorter sides became a helix (but one that didn’t quite wrap all the way around the cylinder). Here was Michael’s animation of this second possible cylinder:

This time, the circumference of the base was 6 rather than 2, which meant 2𝜋r = 6, or r = 3/𝜋 units. And instead of being 6·sin(30°), the height was now 2·sin(30°), or 1. Plugging these values into the formula for the volume, you got 𝜋r²h = 𝜋·(3/𝜋)²·1 = 9/𝜋 cubic units.

In summary, two volumes were possible for the right cylinder, depending on which pair of opposite edges you furled together. These volumes were 3/𝝅 and 9/𝝅, and I accepted any solution that provided at least one of these.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Isabella Ho and Summer Kang 🎻 from San Francisco, California. I received 27 timely submissions, of which 26 were correct—good for an impressive 96 percent solve rate.

For Extra Credit, you had a parallelogram with an area of 1 square unit. Let V represent the average volume of all cylinders whose lateral surface you could neatly make by swirling two edges of the parallelogram together.

What was the minimum possible value of V?