Can You Make a Toilet Paper Roll?

When you unfurl a toilet paper roll, you get a parallelogram of cardboard. If, instead, you furl a parallelogram, what size toilet paper roll can you make?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

From one of my kids comes a question worth pondering … on the toilet:

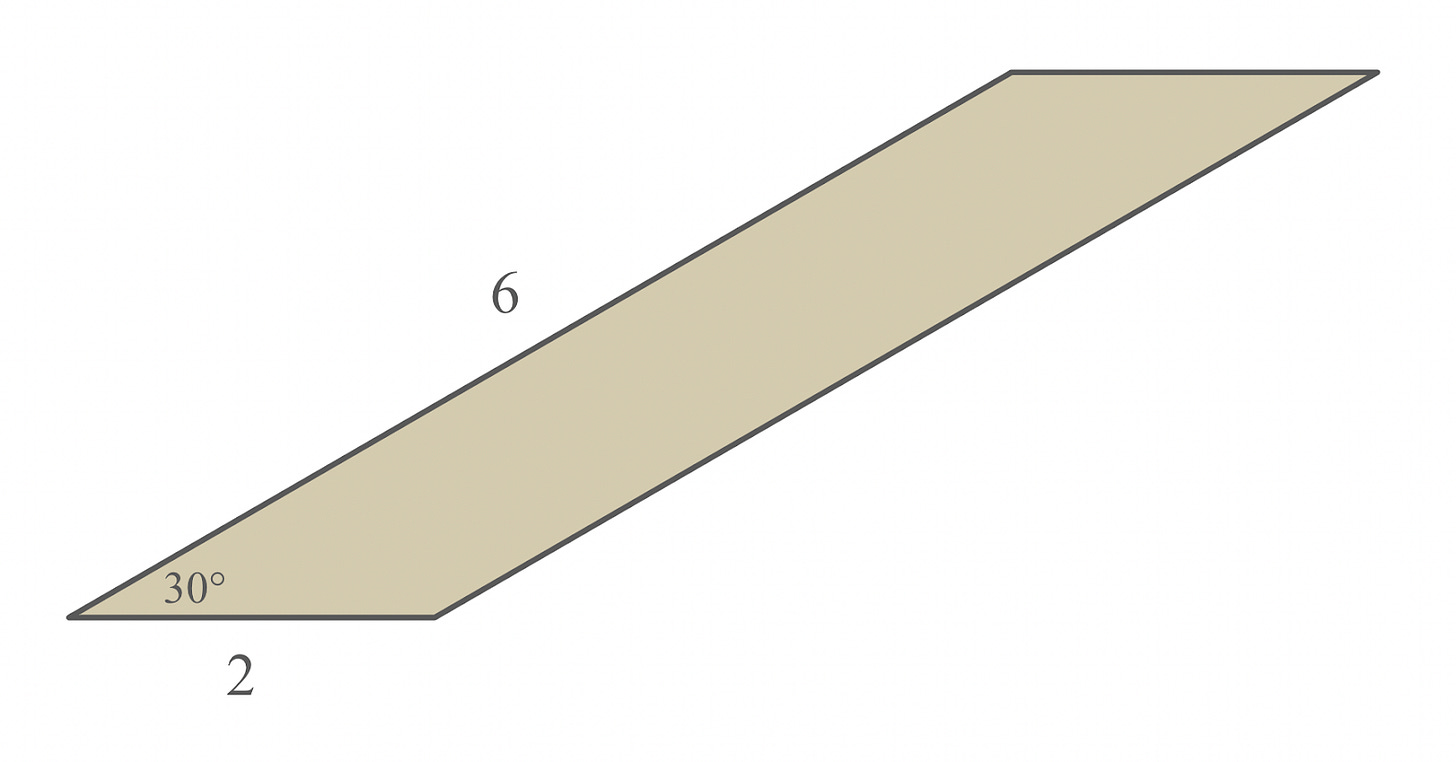
Suppose you have the parallelogram of cardboard shown below, which has side lengths of 2 units and 6 units, and angles of 30 degrees and 150 degrees:

By swirling two edges together, it’s possible to neatly (without any overlap) generate the lateral surface of a right cylinder—in other words, a toilet paper roll! (If you’re not convinced, try gently tearing a toilet paper roll along its diagonal seam and then unwrapping it into a flat shape. You get a parallelogram!)

Determine the volume of a cylinder you can make from this particular piece of cardboard.

This Week’s Extra Credit

Suppose you have a parallelogram with an area of 1 square unit. Let V represent the average volume of all cylinders whose lateral surface you can neatly make by swirling two edges of the parallelogram together.

What is the minimum possible value of V?

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a puzzle from Alex Bellos over at The Guardian. I think it’s a fantastic puzzle, but I’m tweaking the wording to make it a little clearer:

You’re playing five-card stud poker against a single opponent. Which of the following two hands would you rather be dealt?

• Ace, Ace, Ace, King, King

• Ace, Ace, Ace, Nine, Nine

According to Alex, this “poker puzzle is one of [his] favorites. [He has] never met anyone who has got[ten] it right.” Maybe you’ll be the first?

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Nate McIntosh 🎻 from Toledo, Ohio. I received 32 timely submissions, of which 19 were correct—good for a 59 percent solve rate.

Last week, you played a simplified version of Shut the Box, in which there were six initially unflipped tiles (numbered 1-6) on the side of a box. You rolled a fair, six-sided die, after which you could flip down any combination of unflipped tiles that added to the roll. For example, if you rolled a 5, you could have flipped down the 5, the 1 and the 4, or the 2 and the 3. You proceeded until no set of flips was possible (e.g., you rolled a 3 but your only remaining tiles were 2 and 6). To win, you had to flip down all six tiles.

Assuming you played with an optimal strategy (i.e., maximizing your chances of winning after any given roll), what was the probability that you would win?

To flip down a larger number (e.g., 5), you had to actually roll at least that value (e.g., 5 or 6). Since those didn’t come around too often, it made sense for your strategy to flip over the highest number you possibly could. Smaller numbers (e.g., 1 and 2) could often be flipped whether your roll was high or low, so it made sense to save them for later.

Several solvers attempted to explore this sort of “greedy” strategy by listing out the sequences of rolls that would result in victory. All of these sequences had to sum to 21 (the sum of the numbers from 1-6) and had to include at least one 6 (in order to flip the 6).

For example, any ordering of 1, 2, 3, 4, 5, and 6 resulted in a win. The probability of getting these six different rolls in six tries was 6!/6⁶, or about 1.54 percent.

But other combinations of rolls were trickier to analyze, such as the orderings of 1, 4, 5, 5, 6. If that had been the actual order of the rolls, then you would have flipped the 3 and the 2 when you rolled the second 5, resulting in victory. But if the order had instead been, say, 5, 5, 4, 1, 6, then you would have had a problem. After the first roll you’d flip over the 5. After the second roll you’d flip over the 4 and the 1. After the third roll … you were stuck, as there was no way to make 4 from the unflipped tiles 2, 3, and 6.

Thus, listing out all the “winning” sequences was incredibly tricky work, and typically resulted in answers that were slightly off one way or the other due to undercounting or overcounting the cases.

An alternative computational approach to test out all possible six-roll sequences. (Why six rolls? Because you had to flip at least one tile per roll, and there were six tiles.) That meant there were 6⁶, or 46,656, sequences to consider. For each case, your code flipped over tiles based on what was still there, with higher tiles receiving greater priority. For example, if you rolled a 6, your code first tried to flip over the 6. If that had already been flipped, it next tried the 5 and the 1. If at least one of those had already been flipped, it next tried the 4 and the 2. If at least one of those had already been flipped, it tried the 3, the 2, and the 1. And if at least one of those had been flipped, then you lost the game.

Proceeding in this fashion through all 46,656 cases, it turned out that 3,480 of them resulted in victory. That suggested the answer was 3480/46656, which simplified to 145/1944, or about 7.46 percent.

This was the best our greedy strategy could do, and it represented a lower bound on the actual solution to the puzzle. But it was still possible that a less greedy strategy might have done better. For example, when rolling a 6, what if you tried flipping over the 4 and the 2 before flipping over the 5 and the 1? Would that have resulted in a greater chance of victory?

To figure this out, solvers like David Kravitz and Michael Schubmehl made their computers work even harder. Using recursion or dynamic programming, they had their computers figure out, given the current state of flipped versus unflipped tiles, which remaining tiles should be flipped for any given roll.

Such techniques tended to work backward. For example, if only the 5 tile was unflipped and you rolled a 5, it was clear you should flip the 5. But if 1, 2, 3, and 4 were all unflipped when you rolled a 5, the program analyzed whether you were more likely to win from a state where 1 and 4 remained unflipped (i.e., you had flipped the 2 and the 3) or a state where 2 and 3 remained unflipped (i.e., you had flipped the 1 and the 4).

After all this number crunching, your probability of winning when all six tiles were initially unflipped was … drumroll, please … 145/1944. Yes, the greedy strategy of always flipping the highest number possible was also an optimal strategy! Table I from solver Eric Widdison’s write-up included the detailed strategy of which tiles to flip given the current state and roll. (Before you ask, yes, there was a Table II and a Table III, but more on those later.)

A benefit of working out the answer via dynamic programming was that it also gave you the probability of winning from any particular state of flipped tiles. That, in turn, allowed you to answer some other interesting questions.

For example, assuming at least one tile remained unflipped, which state gave you the best chance of winning? That was when the 1, 2, and 3 tiles all remained unflipped, at which point you had a solid 1-in-3 chance of victory. And which state gave you the worst chance? That was when the 3, 4, 5, and 6 tiles all remained unflipped, at which point you had a measly 1-in-54 chance of victory.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Michael Coffey 🎻 from Melbourne, Australia. I received 18 timely submissions, of which 17 were correct—good for a 94 percent solve rate. In other words, if you were confident enough to submit a solution, you probably knew exactly what you were doing.

For Extra Credit, you played a standard game of Shut the Box. This time around, you were rolling two fair, six-sided dice, and there were initially nine unflipped tiles (numbered 1-9). To win, you had to flip down all nine tiles.

Assuming you played with an optimal strategy, what was the probability that you would win?