Can You Take the Scenic Route?

You want to drive around a circular loop. But there’s just one gas station, and a full tank only gets you halfway around. Can your friends help you make it all the way around?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

From Sanandan Swaminathan comes a logic puzzle about a picturesque drive, and getting by with a little help from your friends:

There is a circular road, along which travelers can drive in either direction. However, there is only one gas station on the loop. Driving the full loop in your car requires 40 gallons of gas, but your car’s fuel tank has a maximum capacity of 20 gallons. That said, you’d love to see every last spot along the route.

Of course, you can’t achieve this with just your own car. Fortunately, you can call on any number of your Fiddler Nation friends, all of whom happen to have the same make and model car as you, each with a 20-gallon fuel tank and identical fuel efficiency.

Now, all the cars, including yours, must start and end at the gas station. However, only your car must cover the entire route. The gas station can be visited (and refueled at) by any car, any number of times. Cars may also transfer fuel from one to another, provided they meet up together at a spot along the route.

What is the smallest number of cars (including yours) needed for you to see every spot on the circular route?

(Note: There’s no “cheating” here. No towing or pushing of cars. Every car must be driven on its own, and by one person. No jerrycans for lugging around extra fuel, and so on and so forth.)

Extra Credit

Assuming you’ve used the smallest number of cars to complete your tour of the entire circular road, Sanandan offers the following as Extra Credit:

What is the minimum amount of gas collectively needed by all cars for this journey? (Remember, all the cars must begin and end at the gas station.)

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a recent column from Alex Bellos over at The Guardian. (No spoilers in the link this time!)

The column features three word puzzles of increasing difficulty. For each puzzle, you must determine eight letters arranged in a column. You are also given six clues, each of which applies to three letters within the column that spell out a word suggested by the clue.

The second half of Alex’s column connects these puzzles to work in computational complexity theory. Definitely worth a read!

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winners from last week: 🎻 Brett and Xavier Kiefer 🎻 from Honolulu, Hawaii. I received 51 timely submissions, of which 50 were correct—good for a staggering 98 percent solve rate!

Last week, you and two friends were celebrating your birthdays together with one big cake that had delicious frosting around its perimeter. To share the cake fairly, you wanted to ensure that (1) each of you got the same amount of cake, by area, and (2) each of you got the same amount of frosting along the cake’s edge.

What’s more, you wanted to cut the cake by starting at a single point inside of it, and then making three straight cuts to the edge from that point. You had already worked out ways to do this for circular and square cakes, as shown below.

However, the cake you bought was rectangular, with a length of 20 inches and a width of 10 inches. Using the coordinate system of your choice, you had to describe a way this particular cake could be cut fairly, so that all three of you got the same amount in terms of both area and the cake’s perimeter.

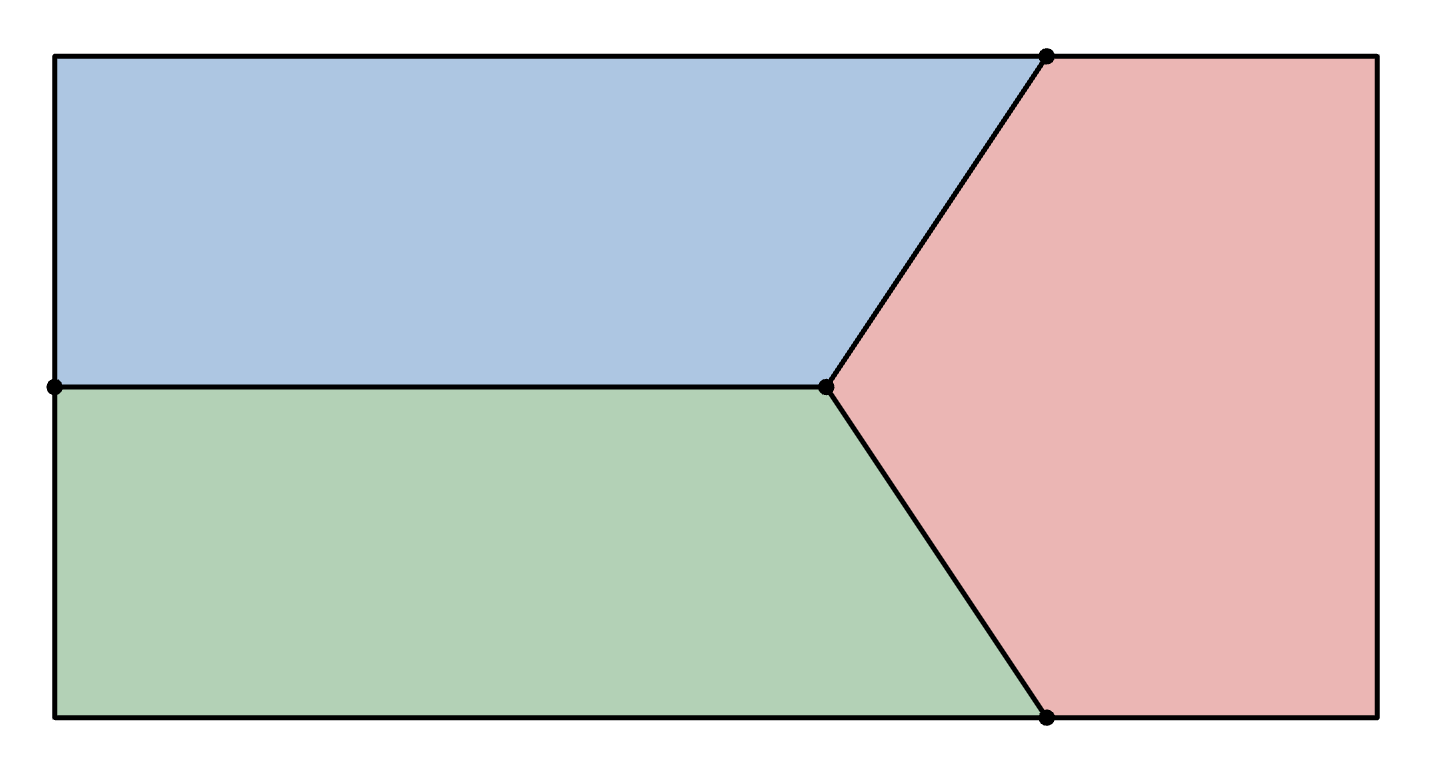
There were two solutions that made up the vast majority of the submissions. First, many solvers split the cake like this:

There were two congruent trapezoids (shown in blue and green) and a pentagon (shown in red). Also, the internal point from which all three cuts emanated was vertically centered. That left two degrees of freedom: (1) the horizontal position of the point from which the cuts emanated, and (2) the lengths of the two parallel sides of the pentagon.

Let’s suppose the length of the edge shared by the two trapezoids was x, while the length of the two parallel sides of the pentagon was y. By plugging these two variables into equations for area and the cake’s perimeter, it was possible to determine specific values of x and y that resulted in a fair cut.

First, let’s look at perimeter. All three pieces had to have a length of frosting equal to one third of the rectangle’s perimeter, or 20. You could have analyzed any of the three pieces; here, let’s look at the red pentagon. It had three edges from the original rectangle: one of length 10, the other two of length y. Setting 10+2y equal to 20 meant y was 5. One variable down, one to go!

Next, let’s look at area. All three pieces had the same area, which was 200/3. Again, you could have analyzed any of the three pieces; this time, let’s look at the blue trapezoid. Its bottom base had length x, while its top base had length 15 (now that you knew y was 5). Its height was 5. Plugging these values into the formula for the area of a trapezoid gave you the equation 5·(x+15)/2 = 200/3. Solving this gave you x = 35/3, or 11 and 2/3.

If the bottom left corner of the rectangle was the origin, then the point from which the cuts emanated was (35/3, 5), and the cuts extended from there to the points (0, 5), (15, 0), and (15, 10).

The other popular solution looked a little different:

Once again, there were two congruent trapezoids (shown in blue and green). But instead of a pentagon, there was now an isosceles triangle (shown in red). This time, the point from which the cuts emanated was horizontally centered, which left a single degree of freedom: the height of the triangle, which we’ll call z.

These three pieces definitely had the same amount of frosting, since the triangle had one side of length 20 from the rectangle, while the trapezoids each had two edges of length 10 from the rectangle.

As for area, the triangle had a base of 20 and a height of z, so its area was 10z. Setting this equal to 200/3 meant z was 20/3.

If the bottom left corner of the rectangle was the origin, then the point from which the cuts emanated was at (10, 20/3), and the cuts extended from there to the points (0, 0), (20, 0), and (10, 10).

As I said, these were the two most popular solutions. Of course, there were others, as we’ll see in the Extra Credit below.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Michael Bradley 🎻 from London, England. I received 39 timely submissions, of which 23 were correct—good for a 59 percent solve rate.

As it turned out, there were many possible central points from which you could fairly cut the 20-inch by 10-inch rectangular cake. Together, these points formed a locus that was a closed shape. 

For Extra Credit, what was the area contained within this shape?