Can You Fairly Cut the Birthday Cake?

It’s one thing for everyone to get the same amount of cake. But can everyone also get the same amount of frosting around the cake's edge?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

For all those special people who have birthdays this month, here’s a fun geometry puzzle from Friend-of-The-Fiddler Dean Ballard:

You and two friends all have March birthdays, so you’ve decided to celebrate together with one big cake that has delicious frosting around its perimeter. To share the cake fairly, you want to ensure that (1) each of you gets the same amount of cake, by area, and (2) each of you gets the same amount of frosting along the cake’s edge.

What’s more, you want to cut the cake by starting at a single point inside of it, and then making three straight cuts to the edge from that point. You’ve already worked out ways to do this for circular and square cakes, as shown below.

However, the cake you bought is rectangular, with a length of 20 inches and a width of 10 inches. Using the coordinate system of your choice, describe a way this particular cake can be cut fairly, so that all three of you get the same amount in terms of both area and the cake’s perimeter. Again, there should be three straight cuts emanating from a single point inside the cake.

To be clear, the three pieces themselves need not have the same perimeter. Instead, each piece must have the same amount of the perimeter from original, uncut cake.

Extra Credit

By now, you’ve hopefully found at least one central point from which you can make your three straight cuts, so that you and your two friends each get the same amount of birthday cake, in terms of both area and the frosting along the edge.

As it turns out, there are many possible central points from which you can fairly cut the 20-inch by 10-inch rectangular cake. Together, these points form a locus that’s a closed shape. 

For Extra Credit, what is the area contained within this shape?

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m delighted to share that Catriona Agg recently posted two brand new felt-tip geometry puzzles. Here are direct links to the first and second of these puzzles, but be wary of spoilers!

For a spoiler-free experience, I’m sharing Catriona’s drawings below.

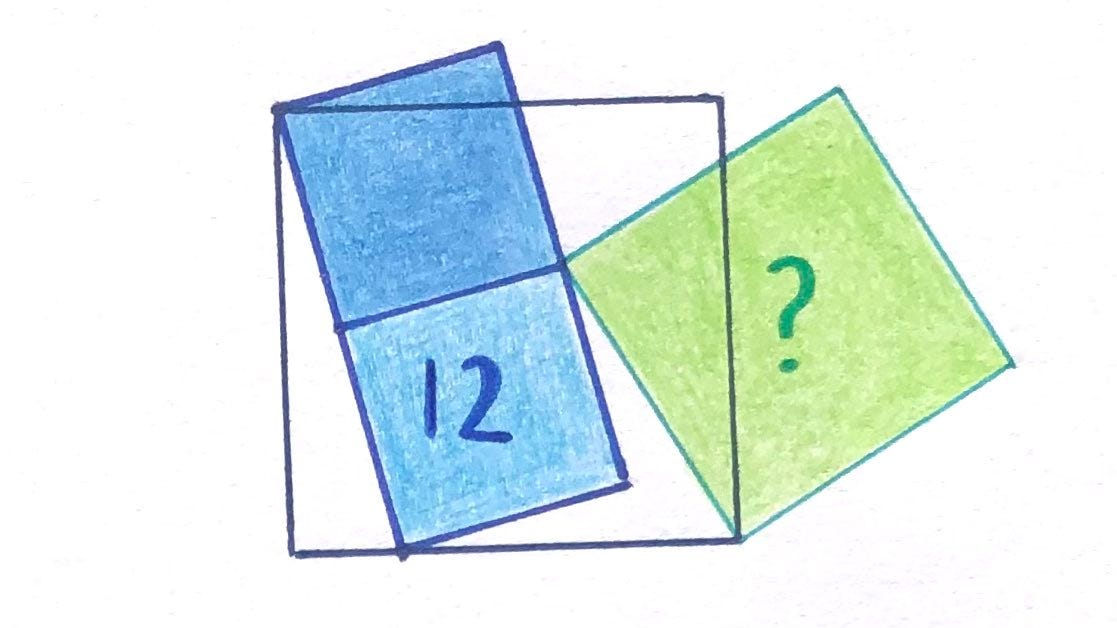
“Four squares. What’s the green area?”

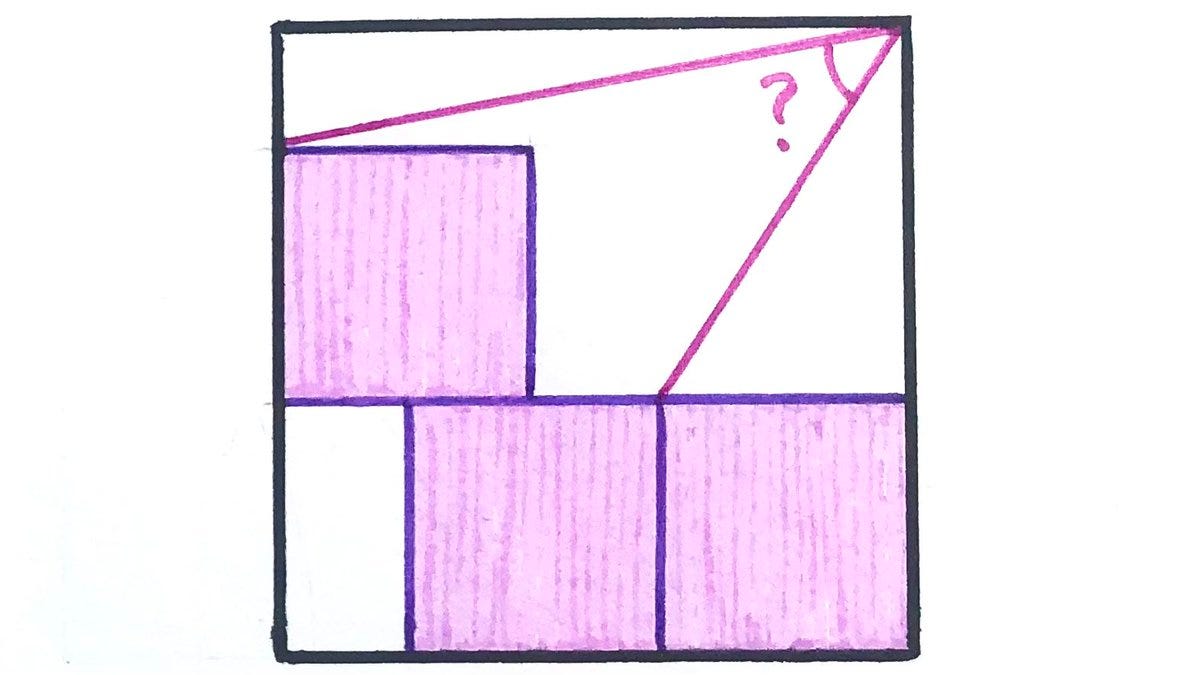
“The three smaller squares are the same size. What’s the angle?”

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Will Apostolides 🎻 from Mechanicsville, Virginia. I received 72 timely submissions, of which 70 were correct—good for a 97 percent solve rate. That’s a new record high solve rate for a Fiddler (excluding the Extra Credit). Great job, everyone!

Last week, you tried your hand at coaching in a Super Bowl headed into overtime. Every time either team was on offense, there was a 1-in-3 chance they scored a touchdown (worth a total of 7 points, as we didn’t bother with 2-point conversions here), a 1-in-3 chance they scored a field goal (worth 3 points), and a 1-in-3 chance they didn’t score any points (i.e., they punted or turned the ball over on downs).

Now, here’s how overtime worked: Your team was on offense first. No matter how many points your team did or did not score, the other team then got a chance at offense. If the game was still tied beyond this point, the teams continued alternating between offense and defense. Whichever team scored next won immediately.

Again, your team was on offense first. What was your team’s probability of winning?

Let’s take this case by case, and see what happens. Suppose your team scored a touchdown first, which occurred with probability 1/3. If your opponent scored a field goal or didn’t score (with combined probability 2/3), you won! But if they scored a touchdown, the game went to “sudden death,” a colloquial way of saying that the next team to score won immediately.

Let’s pause for a moment and figure out what your team’s chances of winning sudden death were, provided you were on offense first. Upon entering sudden death, your team scored either a touchdown or a field goal with probability 2/3, in which case you won. But your team didn’t score with probability 1/3, after which you needed your opponent to similarly not score, also with probability 1/3. After that, you found yourself again winning with probability 2/3, or else you didn’t score and you needed your opponent to similarly not score. (Every time you didn’t score, you needed your opponent to also not score, after which the process repeated itself.) Multiplying the probabilities within each case together, and then adding up the resulting products, your chances of winning sudden death were 2/3 + (1/3)²·(2/3) + (1/3)⁴·(2/3) + (1/3)⁶·(2/3) + …, a geometric series! The sum of any convergent geometric series is the first term divided by one minus the ratio between successive terms. Here, that came to 2/3 ÷ 8/9, or 3/4. In other words, upon reaching sudden death, you had a 75 percent chance of winning.

Okay, now back to your team scoring a touchdown on the first drive in overtime. Again, you won if your opponent couldn’t match your touchdown, and the probability of all this was (1/3)·(2/3), or 2/9. But if you both scored touchdowns, then it went to sudden death. The probability of this scenario—and your winning it—was (1/3)·(1/3)·(3/4), or 1/12. In total, initially scoring a touchdown contributed 2/9 + 1/12, or 11/36, to your probability of winning.

Instead of an opening touchdown, what if your team scored a field goal (probability 1/3)? You won if your opponent then didn’t score (probability 1/3), or if they too scored a field goal and it went into sudden death (probability 1/3) that you then won (probability 3/4). Putting these together, initially scoring a field goal contributed (1/3)·(1/3) + (1/3)·(1/3)·(3/4), or 7/36, to your probability of winning.

Finally, what if your team didn’t score on its opening drive of overtime (probability 1/3)? You needed your opponent to similarly not score (probability 1/3), after which you needed to win in sudden death (probability 3/4). That meant initially not scoring contributed (1/3)·(1/3)·(3/4), or 1/12, to your probability of winning.

Adding these all together—the cases in which you initially scored a touchdown, a field goal, or turned the ball over—meant your probability of winning was 11/36 + 7/36 + 1/12, which simplified to 7/12, or about 58.3 percent. By starting on offense, you were more likely to win than your opponent was!

By the way, the classroom in Mechanicsville (which included this week’s winner, Will) arrived at the same conclusion, as shown in the photo below:

As I mentioned in last week’s puzzle, San Francisco’s coach indeed opted to be on offense first during overtime of the most recent Super Bowl. Nevertheless, his team lost, resulting in some criticism. Of course, when you expect to win 58.3 percent of the time, you should expect to lose 41.7 percent of the time, which is to say, quite often.

At the same time, the model for this puzzle—equal probabilities for scoring a touchdown, a field goal, and turning the ball over, and without any 2-point conversions—was rather simple. Perhaps adding more complexity to the model, so that it better represented a real football game in overtime, would reveal that being on offense first held less of an advantage (or even a disadvantage). For that, we turn to the Extra Credit!

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Adam DeBruler 🎻 from Atlanta, Georgia. I received 45 timely submissions, of which 35 were correct—good for a 78 percent solve rate.

For Extra Credit, you were still a coach at the Super Bowl, but now both teams could choose between two offensive strategies with each possession. They could still opt for a strategy that resulted in 7 points, 3 points, or 0 points, each with a 1-in-3 chance. Alternatively, they could opt for a more aggressive strategy that resulted in 7 points or 0 points, each with a 1-in-2 chance.

Why include this second strategy? If your team happened to score a touchdown on its first possession, then it didn’t make sense for your opponent to then attempt a field goal, since they’d be guaranteed a loss. Instead, they would have attempted a tying touchdown at all costs.

Once again, your team was on offense first. Assuming both teams played to maximize their own chances of a Super Bowl victory, what was your team’s probability of winning?