How Many Loops Can You Slither Around?

Warning: This week’s puzzles may introduce you to an addictive logic game.

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

From Emilie Mitchell comes some loopy fun:

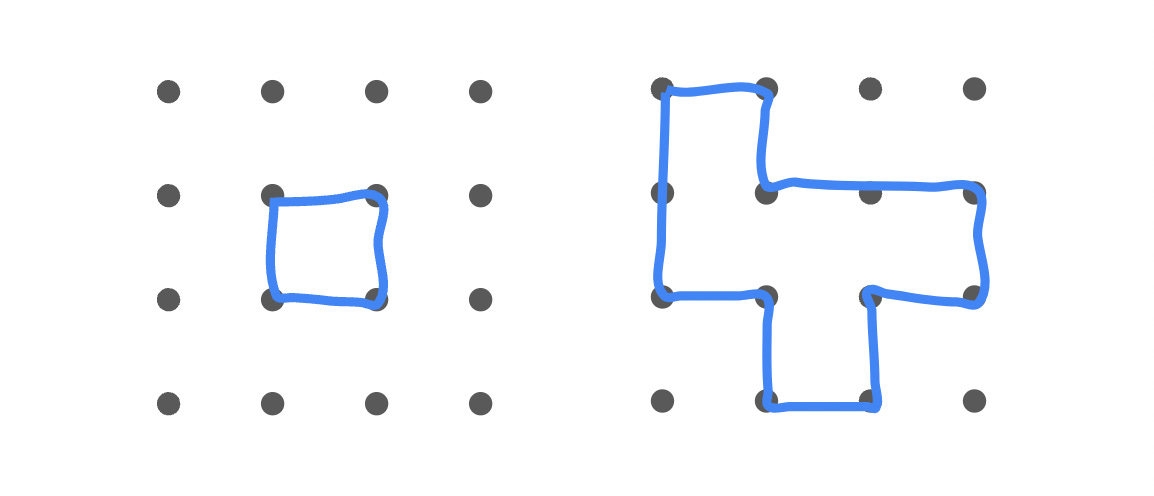
Nikoli the snake wants to slither along a loop through a four-by-four grid of points. To form a loop, Nikoli can connect any horizontally or vertically adjacent points with a line segment. However, Nikoli has certain standards when it comes to loop construction. In particular:

• The loop can never cross over itself.

• No two corners of the loop can meet at the same point.

• Once Nikoli has crossed the connection between two points, Nikoli can’t cross it again (in either direction).

For example, the following two constructions are valid loops:

Meanwhile, the following three constructions are not valid. The one on the left crosses over itself, the one in the middle has two corners that meet at a single point, and the one on the right requires Nikoli to pass over the same line segment twice.

How many unique loops can Nikoli make on the four-by-four grid? (For any given loop, Nikoli can travel in two directions around it. However, these should still be counted as a single loop.)

Extra Credit

From Emilie Mitchell also comes some sneaky, slithery Extra Credit:

Emilie recently introduced me to Slitherlink puzzles. If you too have never played these before, you might want to spend a few minutes getting hooked here or here.

In a Slitherlink, you connect adjacent points in a grid to form a loop that does not self-intersect, as described above. But what makes a Slitherlink a puzzle is that numbers are provided in some of the spaces between four grid points. These numbers specify how many of the four surrounding edges are present in the desired loop. Then it’s entirely up to you to draw the loop.

For example, here’s a puzzle I encountered on one of the previously linked sites, as well as the solution. (I marked red x’s where I knew there couldn’t be any edges—a helpful strategy when solving such puzzles.)

Got all that? Okay, so the Extra Credit is this: How many distinct Slitherlink puzzles can you create on a four-by-four grid of points? Each puzzle consists of a placement of numbers (from 0 to 4) between grid points, and must result in exactly one loop. Note that multiple distinct puzzles can result in the same loop, but again, each puzzle itself can have only one loop solution.

Note: What I’m calling a “four-by-four” grid is technically a “three-by-three” Slitherlink, since the latter describes the array for the numbers, rather than the points. But to keep things consistent between the puzzles this week, I’m steadfastly calling this a “four-by-four” grid.

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a quickie I saw from Michael Jacobs, which I’ll paraphrase (spoiler-free) below:

Each block in the pyramid above is the product of the two blocks below it. At the bottom, a, b, c, and d are distinct whole numbers that are not perfect squares, so that the bottom four blocks are irrational. What values for a, b, c, and d result in a top square that’s a whole number?

I’ll also ask an additional question that wasn’t in the original puzzle statement: What’s the smallest possible whole number value for the top square?

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Morgan Schreffler 🎻 from Peoria, Illinois. I received 120 timely submissions, of which 113 were correct—good for an impressive 94 percent solve rate. Better yet, this was a new record number of solvers for any puzzle here at The Fiddler. Nice job, everyone!

Last week, for any positive, base-10 integer N, we defined f(N) as the number of times you had to add up its digits until you got a one-digit number. For example, f(23) = 1 because 2+3 = 5, a one-digit number. Meanwhile, f(888) = 2, since 8+8+8 = 24, a two-digit number, and then adding up those digits gave you 2+4 = 6, a one-digit number.

Your task was to find the smallest whole number N such that f(N) = 4.

To figure this out, a good strategy was to start small and work your way up. First off, there were nine positive integers N such that f(N) = 0: 1, 2, 3, 4, 5, 6, 7, 8, and 9. So far, so good.

Next, there were infinitely many integers N such that f(N) = 1. (Well, that escalated quickly.) Any number whose digits added up to 1, 2, 3, 4, 5, 6, 7, 8, or 9 fell into this category. The smallest such numbers were 10, 11, 12, 13, 14, 15, 16, 17, 18, 20, 21, 22, 23, 24, 25, 26, 27, 30, 31, 32, 33, 34, 35, 36, 40, etc.

Notably, there were a few numbers missing from that sequence. Where were 19, 28, 29, 37, 38, 39, and so on? Well, the sum of their digits was 10 or greater, which meant these values of N had f(N) = 2. The smallest of these was 19: 1+9 = 10, and then 1+0 = 1.

The key insight to solving this puzzle was to recognize that if f(N) equaled some value k, then applying f to any number whose digits added up to f(N) gave you k+1. For example, to find N such that f(N) = 3, you needed the sum of N’s digits to be somewhere on that list where f(N) = 2. In other words, N’s digits had to add up to 19, 28, 29, 37, 38, 39, etc. First-time solver Will Roberts, who teaches 7th grade mathematics, made this insight on a break between parent teacher conferences. Way to go, Will!

Okay, so then what were some numbers whose digits added up to 19? The smallest of these were 199, 289, 298, 379, 388, 397, and so on. Meanwhile, the first few numbers whose digits added up to 28 were 1999, 2899, 2989, 2998, 3799, and so on.

Continuing this strategy, you could find numbers N such that f(N) = 4 by looking for numbers whose digits added up to 199, 289, 298, etc. These were some pretty big sums, so your best best was to find a number whose digits added up to the smallest of these—199. The smallest such number was 19,999,999,999,999,999,999,999, which could equivalently be described as “a one followed by 22 nines” or 2×10²²−1, which was indeed the answer to the puzzle. Why? Because 1 + 22×9 was equal to 199, and f(199) = 3.

Several solvers, including Brennan Taylor and Ed Parks, noted that there was an OEIS sequence (isn’t there always?) with the smallest natural numbers such that f(N) = 0, f(N) = 1, f(N) = 2, f(N) = 3, f(N) = 4, etc. It turns out there’s an elegant name for this function f—it’s a number’s “additive persistence.” (By the way, that OEIS page includes a link to an article on multiplicative persistence, which seems like good fodder for another puzzle at some point.)

The next number in the sequence, that is, the smallest value of N such that f(N) = 5, was a one followed by 2,222,222,222,222,222,222,222 nines. Suffice it to say that this sequence grows very quickly.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Justin Vitanza 🎻 from Chicago (who, it turns out, is the Puzzle Pusher over on YouTube). I received 78 timely submissions, of which 70 were correct—good for a 90 percent solve rate. And you know what? That set a record for most solvers for an Extra Credit. What a week it was!

For Extra Credit, you were again analyzing the function f(N). For how many whole numbers N between 1 and 10,000 (inclusive, not that it matters) did f(N) = 3?