Can You Sprint to the Finish?

This year’s Tour de France may already be decided. But the Tour de Fiddler remains in need of some serious solving!

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. The “Extra Credit” is where the analysis typically gets hairy, or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

Every summer I try to run a cycling-related puzzle to coincide with the Tour de France. Previous puzzles have involved the team time trial, “King of the Mountain” points, the shape of the peloton, being paced up a climb, and last year’s catching the breakaway.

This time around, you and a competitor are approaching the finish of a grueling stage of the Tour de Fiddler. One of you will win the stage, the other will come in second. As you approach the finish, each of you will test the feeling of your legs, which will be somewhere between 0 percent (“I can barely go on!”) and 100 percent (“I can do this all day!”). For the purposes of this puzzle, these values are chosen randomly, uniformly, and independently.

Immediately after feeling your legs, you and your opponent each have a decision to make. Do you maintain your current pace, or do you sprint to the finish? Among those who sprint for the finish, whoever’s legs are feeling the best will win the stage. But if no one sprints for the finish, everyone has an equal chance of winning the stage. In the Tour de Fiddler, you must each decide independently whether to sprint for the finish based on your legs—you don’t have time to react to your opponent’s decision.

Normally, teams at the Tour de Fiddler keep their strategy and tactics close to the vest. But earlier today, your opponent’s manager declared on international television that if (and only if) your opponent’s legs were feeling 50 percent or better, they’d sprint for the finish.

As you are about to test your legs for the final sprint and see how they feel, what are your chances of winning the stage, assuming an optimal strategy?

This Week’s Extra Credit

Instead of one opponent, now you have two—meaning three riders in total. As luck would have it, the managers for both other riders proclaimed that they’d sprint for the finish if (and only if) their legs were feeling 50 percent or better. Note that your opponents’ feelings are independent of each other.

As the three of you near the finish, your own team manager radios you the following message: “If your legs feel <garbled> percent or better, sprint for the finish!”

You can’t make out what the garbled part of the message is, and you’re too tired to radio back for confirmation. Instead, you somehow muster the energy to randomly, uniformly pick a number between 0 and 100 to fill in the blank from your manager’s message, thereby determining your racing strategy—optimization be damned!

Right before you choose your random strategy and test your legs, what are your chances of winning the stage against both opponents?

Making the ⌊Rounds⌉

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a watershed moment—an AI has earned a gold medal on this year’s International Math Olympiad.

Google’s Gemini Deep Think scored 35 out of 42 points, solving the first five problems on the six-problem exam. Its generated solutions can be found here. Not too shabby!

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Standings

I’m tracking submissions from paid subscribers and compiling a leaderboard, which I’ll reset every quarter. All correct solutions to Fiddlers and Extra Credits are worth 1 point each. Solutions should be sent prior to 11:59 p.m. the Monday after puzzles are released. At the end of each quarter, I’ll 👑 crown 👑 the finest of Fiddlers. If you think you see a mistake in the standings, kindly let me know.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Connor Colombe 🎻 from Austin, Texas. I received 43 timely submissions, of which 30 were correct—good for a 70 percent solve rate.

Last week’s puzzle was a very special collaboration between Fiddler on the Proof and Science News, where the puzzles were also posted.

You and two friends had arranged to meet at a downtown mall between 3 p.m. and 4 p.m. one afternoon. However, you had neglected to specify a time within that one-hour window. Therefore, the three of you would be arriving at randomly selected times between 3 p.m. and 4 p.m. Once each of you arrived at the mall, you were there for exactly 15 minutes. When the 15 minutes were up, you left.

At some point (or points) during the hour, there was a maximum number of friends at the mall. This maximum could have been one (sad!), two, or three. On average, what would you have expected this maximum number of friends to be?

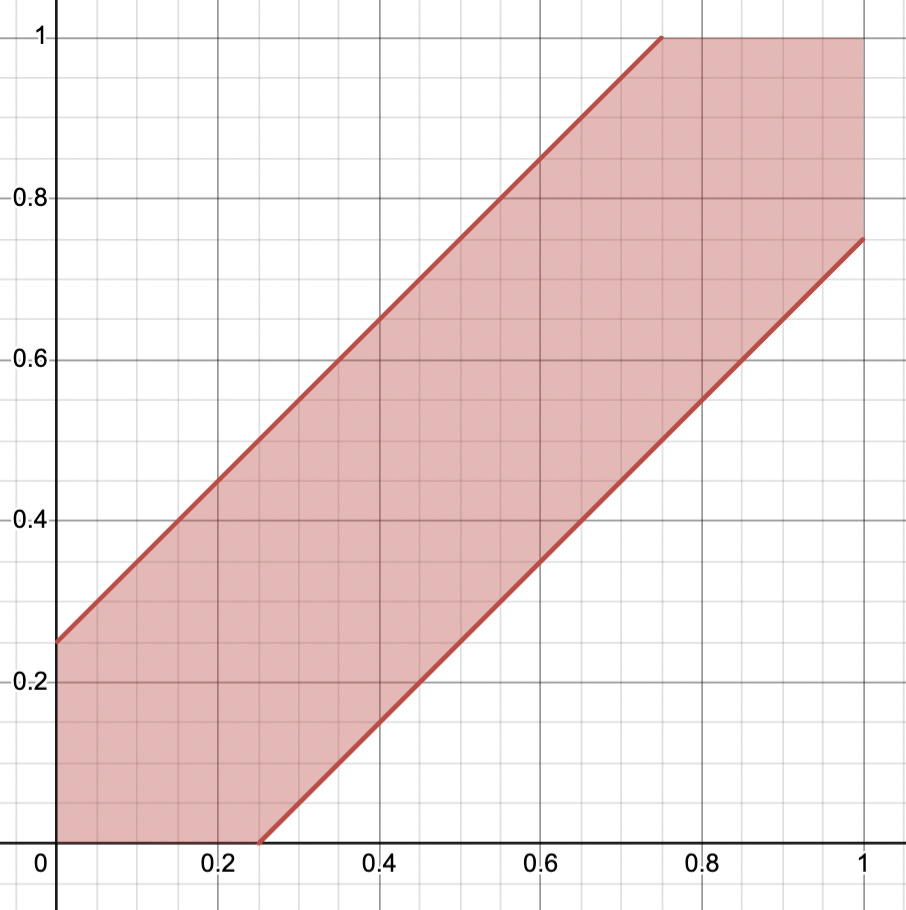
The version of this puzzle with just two friends is fairly well known, but worth revisiting before working our way back up to three friends. In the case of two friends, let x be the time you arrive at the mall (in hours after 3 p.m.), and let y be the time your friend arrives, so that 0 ≤ x, y ≤ 1. The space of possible arrival times to consider is the unit square (shown below). To meet up, the two friends had to arrive within 15 minutes (or one-quarter hour) of each other, a situation represented by the shaded hexagonal region.

You could compute the area of the hexagon by decomposing it or by subtracting from 1 the areas of the two isosceles right triangles on either side. Either way, the hexagon’s area came to 7/16. That meant the maximum number of friends meeting up was two with probability 7/16, and one with probability 9/16. The average was 2·(7/16) + 1·(9/16) = 23/16, or 1.4375.

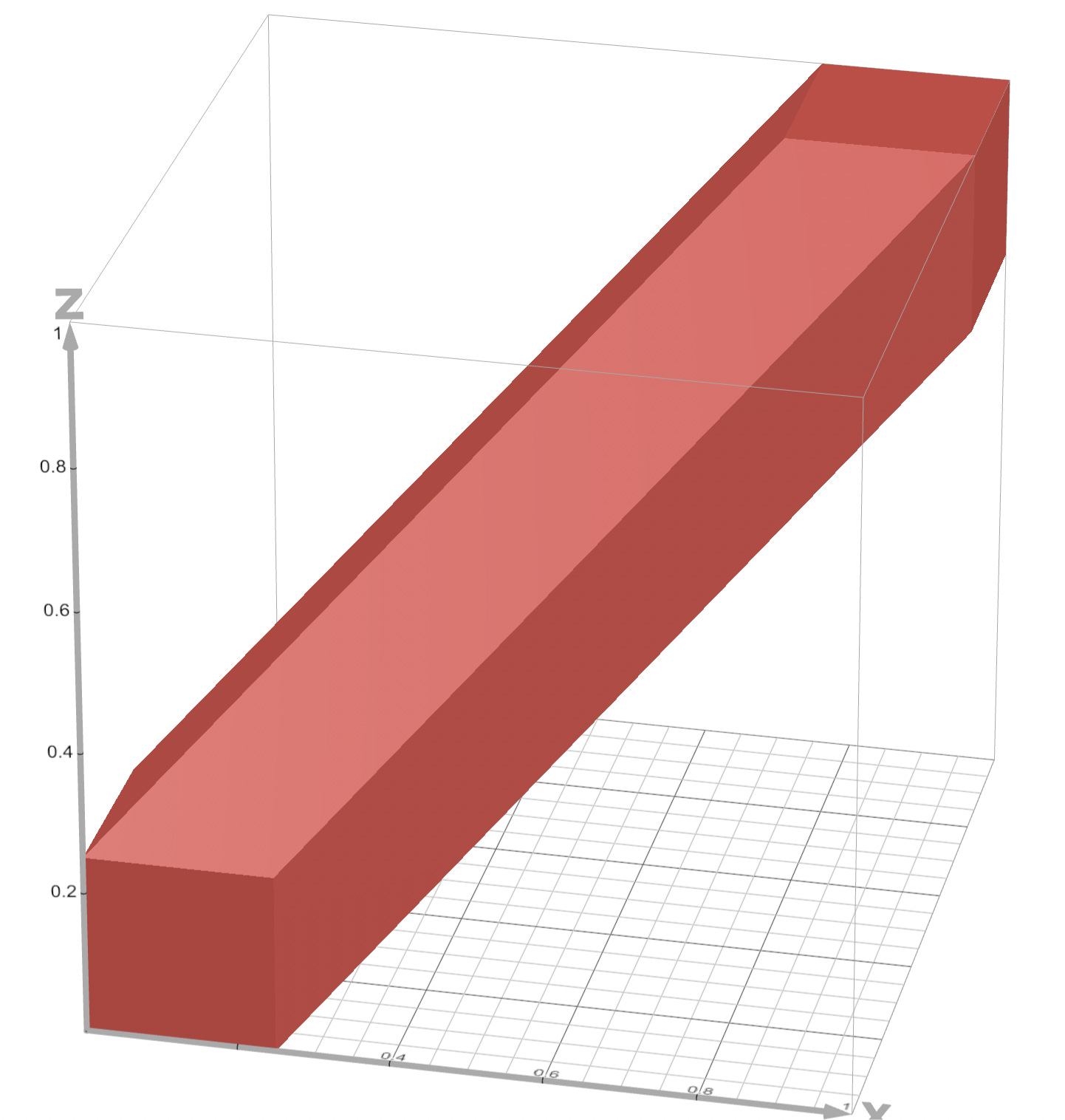
With that out of the way, let’s return to three friends. Instead of a unit square, you now considered a unit cube, with coordinates of x, y and z representing the three arrival times. All three friends met when their arrival times were within a quarter-hour of each other. Mathematically, this could be expressed as three inequalities: |x−y| ≤ 1/4, |y−z| ≤ 1/4, and |z−x| ≤ 1/4. All three of these were true in the region below:

To find the volume of this solid, you could decompose it into a cube of edge length 1/4 in the bottom left, as well as three parallelepipeds coming off three of this smaller cube’s faces. (Similarly, the 2-D case could be decomposed into a square and two parallelograms.) The cube had volume (1/4)³, or 1/64. Each parallelepiped had a square base with area (1/4)², or 1/16, and an altitude of 3/4, for a volume of 3/64. Adding all these volumes together came to 5/32. Note that this was significantly greater than (7/16)³, since the pairwise events of friends meeting up were not independent. (That is, if A met up with B and B met up with C, then it was quite likely that A also met up with C.)

So the probability that all three friends met up was 5/32. Next, we could try to find the probability that two friends met up, but not three. However, that was quite difficult to calculate!

Instead, let’s look at the probability that no friends met each other, so that the maximum number present at any given time was one. Mathematically, that was when the following three inequalities were all true: |x−y| > 1/4, |y−z| > 1/4, and |z−x| > 1/4. Here’s what the 3-D graph of this regime looked like:

It was a collection of six congruent tetrahedra. Each had a base that was a right isosceles triangle with leg length 1/2, and a height of 1/2. So the volume of each was 1/48, which meant their collective volume was 1/8.

If the probability that all three friends met up was 5/32, and the probability that no friends met up was 1/8, then the probability that a maximum of two friends met up was what remained: 1 − 5/32 − 1/8 = 23/32.

The expected maximum number of friends was therefore 3·(5/32) + 2·(23/32) + 1·(1/8) = 65/32, or 2.03125. It was kind of nice that the average was more than just a pair of friends! I awarded credit for all answers that were accurate to at least two decimal places (i.e., 2.03).

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Q P Liu 🎻 from Santa Cruz, California. I received 29 timely submissions, of which 22 were correct—good for a 76 percent solve rate.

Instead of three total friends, now there were four total friends (yourself included). As before, you all arrived at random times during the hour and each stayed for 15 minutes.

On average, what would you have expected the maximum number of friends meeting up to be?