Can You Race Around the Monopoly Board?
Where are you most likely to land? Where are you least likely to land?
Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.
Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.
Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.
I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.
This Week’s Fiddler
Like Monopoly, the game of Oligopoly consists of a square board with 40 individual spaces around it, numbered from 0 to 39. All players begin on space 0 (akin to the “Go” square in Monopoly) and roll a pair of dice to determine how many spaces they advance each turn. However, unlike Monopoly, there is no way to otherwise advance around the board (i.e., there’s no “Chance,” “Community Chest,” going to jail, etc.).
In their first pass around the board, which space from 1 to 39 are players most likely to land on at some point (i.e., not necessarily on their first or last roll, but after any number of rolls)?
Extra Credit
The square Oligopoly board has 10 spaces on each side. The first side has spaces 0 through 9, the second side has spaces 10 through 19, the third side has spaces 20 through 29, and the fourth side has spaces 30 through 39.
Because you’re rolling two dice, it’s impossible to land on space 1 in your first pass around the board. Several other spaces on the first side of the board are similarly unlikely.
Putting that first side of the board aside, which space from 10 to 39 are players least likely to land on at some point during their first pass around the board? (Another question: What if you rolled three dice at a time instead of two?)
Making the Rounds
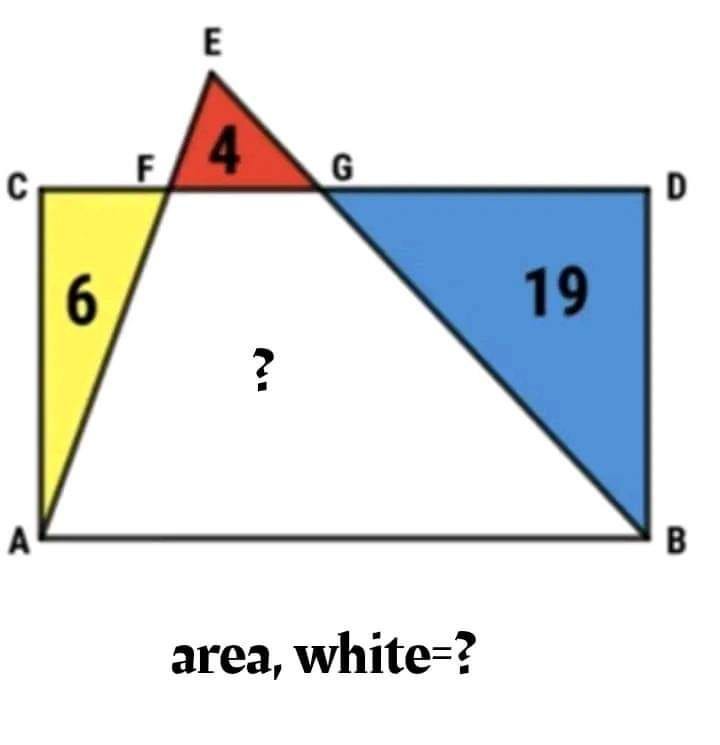
There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a geometric puzzle I encountered a while back. (Spoiler alert: Solutions can readily be found on the thread containing the puzzle. Click the link at your own risk!)
Last Week’s Fiddler
Congratulations to the (randomly selected) winner from two weeks ago: 🎻 Kiera Jones 🎻 from Cincinnati, Ohio. I received 88 timely submissions, of which 78 were correct. That was the third-greatest number of correct answers all-time, and a solid 89 percent solve rate to boot!
When flipping three fair and independent coins, there are four possible outcomes:
You could get three heads, with a probability of 1/8.
You could get two heads, with a probability of 3/8.
You could get one heads, with a probability of 3/8.
You could get zero heads, with a probability of 1/8.
Two weeks ago, you were flipping three such coins, and you did this eight times. What was the probability that you got exactly one occurrence of three heads, three occurrences of two heads, three occurrences of one heads, and one occurrence of zero heads? (Note that these eight occurrences could happen in any order.)
First, let’s pick some order for the results, such as (1) getting three heads, (2) getting two heads, (3) getting two heads, (4) getting two heads, (5) getting one heads, (6) getting one heads, (7) getting one heads, and (8) getting zero heads. What was the probability of getting these results, in this precise order? That was (1/8)·(3/8)·(3/8)·(3/8)·(3/8)·(3/8)·(3/8)·(1/8), or, more compactly, (1/8)2·(3/8)6. Multiplying this out, the probability was 729/16,777,216. Not too likely!
But finding the probability of one such ordering was only half the problem. The second half was figuring out how many of these equally likely orderings there were. There were 8! ways to order the results, but three of these—getting two heads—were equivalent to each other, meaning we overcounted by a factor of 3!, and another three—getting one heads—were also equivalent, meaning we overcounted by another factor of 3!. In total, there were 8!/(3!·3!) distinct ways to order the results.
To find the probability of getting one occurrence of three heads, three occurrences of two heads, three occurrences of one heads, and one occurrence of zero heads—in any order—you had to multiply the number of orderings, 8!/(3!·3!), by the probability of each ordering, (1/8)2·(3/8)6. After a bunch of simplification, this product came to 36·5·7/219, or about 4.8666 percent.
While this probability was still fairly small, it was still the most likely result from eight trials. Indeed, having the ratio of outcomes precisely match the ratio of the probabilities themselves is always the most likely result!
Last Week’s Extra Credit
Congratulations to the (randomly selected) winner from two weeks ago: 🎻 John O'Donoghue 🎻 from Eugene, Oregon (quack!). I received 51 timely submissions, of which 41 were correct. That was the second-greatest number of correct answers for Extra Credits all-time, along with an impressive 80 percent solve rate.
For Extra Credit, you were again flipping three fair and independent coins a total of eight times. Among the four possible outcomes (three heads, two heads, one heads, zero heads), the outcome that happened to occur most frequently—but, importantly, I didn’t saying which one this was!—occurred a times. The next most frequent outcome occurred b times. The next most frequent after that occurred c times. And the least frequent occurred d times. Note that a+b+c+d = 8, and that a ≥ b ≥ c ≥ d. (Yes, equalities were allowed here).
Which ordered quadruple (a, b, c, d) was most likely?
I think half the challenge of this Extra Credit was simply understanding what was being asked. (And I really did try to make it as clear as possible.)
As is often the case, I think it helps to look at an example. In the previous Fiddler, we already analyzed the case of one occurrence of three heads, three occurrences of two heads, three occurrences of one heads, and one occurrence of zero heads. This ratio of 1:3:3:1 was one way to generate the ordered triple (3, 3, 1, 1). But there were other ways, as well. Here were all six of them, along with respective probabilities in parentheses:
three occurrences of three heads, three occurrences of two heads, one occurrence of one heads, and one occurrence of zero heads probability (0.54 percent)
three occurrences of three heads, one occurrence of two heads, three occurrences of one heads, and one occurrence of zero heads (0.54 percent)
three occurrences of three heads, one occurrence of two heads, one occurrence of one heads, and three occurrences of zero heads (0.06 percent)
one occurrence of three heads, three occurrences of two heads, three occurrences of one heads, and one occurrence of zero heads (4.87 percent—the answer to the previous Fiddler!)
one occurrence of three heads, three occurrences of two heads, one occurrence of one heads, and three occurrences of zero heads (0.54 percent)
one occurrence of three heads, one occurrence of two heads, three occurrences of one heads, and three occurrence of zero heads (0.54 percent)
Adding up these six results meant the overall probability of winding up with the quadruple (3, 3, 1, 1) was about 7.1 percent.
But as it turned out, (3, 3, 1, 1) was not the most likely quadruple. Only one of its six permutations was particularly likely, and what’s more, there were just six permutations of the digits 3311 (3311, 3131, 3113, 1331, 1313, and 1133).
So if the answer wasn’t (3, 3, 1, 1), what were the other possible candidates? Well, there were only 15 ordered integer quadruples (a, b, c, d) with a+b+c+d = 8 and a ≥ b ≥ c ≥ d:
(8, 0, 0, 0)
(7, 1, 0, 0)
(6, 2, 0, 0)
(6, 1, 1, 0)
(5, 3, 0, 0)
(5, 2, 1, 0)
(5, 1, 1, 1)
(4, 4, 0, 0)
(4, 3, 1, 0)
(4, 2, 2, 0)
(4, 2, 1, 1)
(3, 3, 2, 0)
(3, 3, 1, 1)
(3, 2, 2, 1)
(2, 2, 2, 2)
For a quadruple to have a high probability of occurring, you wanted all the numbers to be reasonably small, and you also wanted them to be different from each other. If all four numbers were distinct, then they accounted for 4!, or 24, total permutations, as opposed to the measly six permutations of (3, 3, 1, 1).
The likeliest quadruple turned out to be (4, 3, 1, 0), which occurred about 17.5 percent of the time. A few solvers had their computers churn through the combinatorics to calculate this result, while others ran a few million Monte Carlo simulations to see which permutation came out on top. Sure enough, all four values in the quadruple were distinct and relatively small.
Solver 🎬 David Ding 🎬 ran 1 million simulations and plotted the relative frequency of the fifteen possible quadruples, confirming that (4, 3, 1, 0) was our big winner (albeit in rather tiny font):
To wrap things up, I’ll attempt to explain this Extra Credit one more time. If you flip three coins a total of eight times, you are most likely to get one occurrence of three heads, three occurrences of two heads, three occurrences of one heads, and one occurrence of zero heads. (Cool.)
But if you just count how many times you get each of these four possible outcomes and put those four values in a non-increasing ordered quadruple, the most likely result is (4, 3, 1, 0). (Okay, maybe not as cool, but hopefully a little surprising.)
Want to Submit a Puzzle Idea?
Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.





My full write-up, first in a while for me:
https://drive.google.com/file/d/1G9zxvEdzN7xyIhXXF-hFycsgf3raNRFJ/view?usp=drive_link
Nice write-up by Eric Snyder on this one.
I started with statistical simulations to find out what the answers should be. Here's what I got after 2e9 first passes with 1, 2, 3, and 4 dice:
https://i.servimg.com/u/f89/19/74/46/40/oligo10.jpg