Can You Flip the Coins Exactly as You’d Expect?

Sure, you know the odds. But what are the odds of getting precisely those odds?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

Importantly, due to the holidays, there will be no Fiddler next week. The next column will come out on Dec. 1.

This Week’s Fiddler

From Raven Deerwater comes a metapuzzle of coin flipping:

If you flip three (independent) fair coins, there are four possible outcomes:

• You can get three heads, with a probability of 1/8.

• You can get two heads, with a probability of 3/8.

• You can get one heads, with a probability of 3/8.

• You can get zero heads, with a probability of 1/8.

Now suppose you are flipping three coins, and you do this eight times. What is the probability that you’ll get exactly one occurrence of three heads, three occurrences of two heads, three occurrences of one heads, and one occurrence of zero heads? (Note that these eight occurrences can happen in any order.)

Extra Credit

Again, suppose you are flipping three fair and independent coins, and you do this eight times. Among the four possible outcomes (three heads, two heads, one heads, zero heads), the outcome that happens to occur most frequently—but, importantly, I’m not saying which one this is!—occurs a times. The next most frequent outcome occurs b times. The next most frequent after that occurs c times. And the least frequent occurs d times. Note that a+b+c+d = 8, and that a ≥ b ≥ c ≥ d. (Yes, equalities are allowed here).

Which ordered quadruple (a, b, c, d) is most likely?

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing two related puzzles to which reader Bart Wright directed me.

Here’s a statement of the first puzzle:

There are 15 players who will play a cooperative game. They begin by closing their eyes. A referee will place either a black hat or a white hat (chosen by fair coin flip) on each player's head. The players may then open their eyes.

Each hat is visible to every player except the one wearing it. On a signal given by the referee, each player may call out a guess of her own hat color, or may remain silent. The calls are simultaneous.

The players all win if at least one player guesses correctly and nobody guesses incorrectly. They all lose if anyone guesses incorrectly or everybody remains silent.

The players can agree on a strategy beforehand, but no further communication is allowed once the game starts.

Find a strategy for the players that maximizes the probability that they will win. What is that probability?

Got that? Okay, now for the mind-blowing second puzzle that takes this to infinity (and beyond):

Each of an infinite number of wizards is independently assigned a black or white hat based on the outcome of an unbiased coin flip. Each wizard can see everyone's hat but his own.

At the count of three, each wizard must simultaneously either guess his own hat color or abstain from guessing. The wizards collectively win if an infinite number of them guess correctly and none of them guess incorrectly.

Can the wizards devise a strategy so that they usually win?

The wizards can plan and move around before the hats are distributed, but immediately upon hat distribution, a spell is cast so that they are all completely paralyzed up until the moment of their simultaneous guess. No communication is allowed.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Ian Rhile 🎻 from Wyomissing, Pennsylvania. I received 53 timely submissions, of which 51 were correct—good for a 96 percent solve rate, a new record high for a Fiddler. Great work, everyone!

Last week, you had to squeeze two non-overlapping quadrilaterals within a unit circle (i.e., a circle with radius 1). The quadrilaterals could share common edges, parts of edges, or vertices, but their interiors couldn’t overlap. Their vertices could also lie on the circle’s circumference.

What was the greatest combined area these quadrilaterals could have?

To maximize this area, you wanted the quadrilaterals’ combined figure to have lots of sides that could cut into the curvature of the circle, but at the same time you didn’t want lots of space left between those sides.

If the two quadrilaterals didn’t touch at all, they had a combined eight sides—the most you could possibly have. Unfortunately, any such arrangement resulted in lots of empty space outside both quadrilaterals. Similarly, there was lots of unused space when the quadrilaterals shared part of an edge in common.

When they shared a complete common edge, they were able to form convex shapes that better filled the circle. The greatest number of sides they could have together was six (four sides each minus the two sides that were joined together to form an interior). At this point, you had to find the hexagon that optimally filled a circle, which was indeed a regular hexagon.

Solver Dirk Meijer sketched the two quadrilaterals (which turned out to be congruent isosceles trapezoids) that made up the regular hexagon, and computed their combined area, as shown below:

Another way to determine the area was to partition the hexagon into six equilateral triangles with side length 1. With a little 30-60-90 trigonometry, you could show that each triangle had an area of √(3)/4. Therefore, six such triangles had a combined area of 6·√(3)/4, or 1.5√(3). Many solvers rounded this to 2.5981 or even 2.6, or recognized that the regular hexagon made up approximately 82.7 percent of the circle’s area. As long as you gave a valid expression for the area, I gave you full credit.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Michael Schubmehl  🎻 from Hinsdale, Illinois. I received 34 timely submissions, of which 28 were correct—good for an 82 percent solve rate. (The number of solvers of the Extra Credit was once again less than the number of solvers of the Fiddler, restoring a modicum of order to the Universe.)

For Extra Credit, given four distinct points on a unit circle, I defined the quantity Z as the following sum: the area of the (convex) quadrilateral formed by all four of these points plus the area of the largest triangle (by area) formed by any three of these points.

For example, if the four points had been the vertices of an inscribed square, then Z would have been 2—the area of the square—plus 1—the area of the largest triangle formed by three of the points (in this case, the area of any of them)—for a total value of 3.

Given that the four distinct points could have been anywhere on the unit circle, what was the greatest possible value of Z?

One approach was to first reason just what sort of quadrilateral you were dealing with. After that, you’d worry about actually computing the optimal dimensions for the problem.

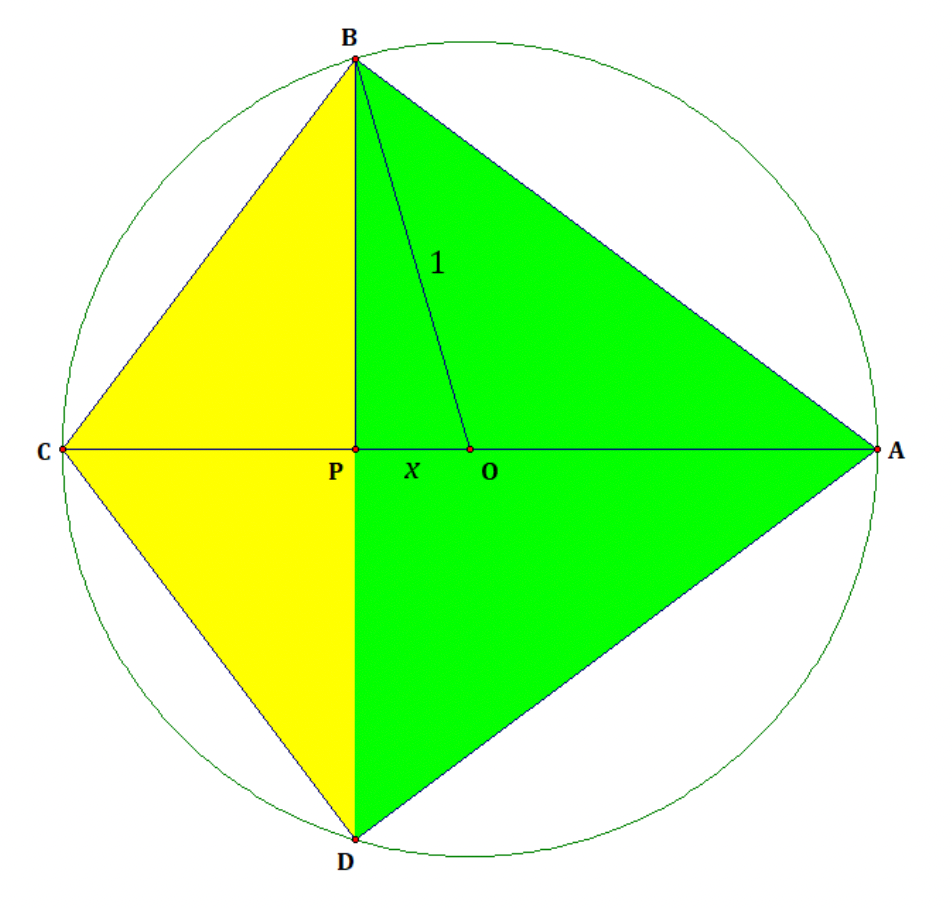
So—what quadrilateral maximized Z? Suppose I came to you with an arrangement of four points and told you they indeed resulted in the maximum value of Z. I even showed you which three points formed the largest triangle by area. Two of these points formed one of the diagonals of the quadrilateral, and let’s call these points B and D. The other point of the largest triangle we’ll call A, and the fourth point we’ll call C.

Now, for triangle ABD, consider the base BD. (Again, that’s an internal diagonal of the quadrilateral.) The area of this triangle (as well as the area of quadrilateral ABCD) was maximized when the altitude from A to side BD was as long as possible. And that happened when A was equidistant from B and D, halfway along the major arc that connected them. Something similar could be said for C—the area of the quadrilateral was maximized (and the area of ABD was unaffected) when C was halfway along the minor arc that connected B and D.

All of this was a fancy way of saying that ABCD was a kite shape (i.e., AB and AD were congruent, while BC and DC were also congruent), and that AC was a diameter of the circle.

Now that you knew the shape of the quadrilateral, you still had to determine the maximum value of Z. At this point, solvers expressed Z in terms of a single variable (e.g., the distance between chord BD and the center of the circle, the measure of arc BC, etc.) and maximized Z expression by setting its derivative with respect to this variable equal to zero.

For example, solver Dean Ballard, called the distance between chord BD and the center of the circle x, as shown below:

By the Pythagorean theorem, BD had length 2√(1−x²). Meanwhile, the altitude from A to BD had length 1+x, which meant the area of triangle ABD was (1+x)√(1−x²). To find the area of quadrilateral ABCD, you had to add this area to that of triangle BCD, which was (1−x)√(1−x²). Putting it all together, Z(x) = (3+x)√(1−x²).

From there, I’m sure I’ll disappoint at least a few readers in skipping over the calculus. The value of Z was maximized when x was approximately 0.281, and this maximum value itself was approximately 3.1488. As several solvers noted, this was amusingly close to 𝜋.

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.