Can You Pour the Water?

The last time a specific friend of mine tried a math puzzle, it was about pouring water among pitchers of various volumes. This week, his time has come again.

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

Last weekend, I saw an old friend of mine (in fact, he was the composer of an opera I performed in several decades ago!) who recently subscribed to The Fiddler. He confessed that the last time he encountered math puzzles like these, they were water pouring puzzles. “Oh, I can do one of those!,” I exclaimed.

So Joel, this week’s puzzle is dedicated to you!

I have two large pitchers with known volumes: 10 liters (“pitcher A”) and 3 liters (“pitcher B”). They are both initially empty. I can do one of six things with the pitchers:

1. I can fill pitcher A to the top with water from the sink.

2. I can fill pitcher B to the top with water from the sink.

3. I can empty the contents of pitcher A into the sink.

4. I can empty the contents of pitcher B into the sink.

5. I can transfer the contents of pitcher A to pitcher B, until pitcher A is empty or pitcher B is filled to the top—whichever comes first.

6. I can transfer the contents of pitcher B to pitcher A, until pitcher B is empty or pitcher A is filled to the top—whichever comes first.

Every time I do any one of the above six, it counts as a step.

What is the fewest number of steps required until one of the pitchers (either A or B) contains precisely 5 liters of water?

Extra Credit

Instead of 10 liters and 3 liters, suppose the volumes of the pitchers A and B are now 100 liters and 93 liters, respectively.

Further suppose that the fewest number of steps needed until one of the pitchers (either A or B) contains precisely N liters of water is f(N), where N is a whole number between 1 and 100, inclusive.

What is the maximum value of f(N), and for which value of N does this occur?

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a so-called (Monty Hall-like) “paradox” with playing cards from the one and only Martin Gardner. This paradox was contained within an article chock-full of such nuggets.

Suppose you shuffle a standard deck and deal out three cards, which you place face down. The plan is for your friend to look at the cards and then turn over two cards that are the same color. Once your friend has done this, Martin asks: “What’s the probability the remaining face-down card is the same color as the two face-up cards?”

Hint: It’s not 50 percent!

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Jason Weisman 🎻 from Wilton, Connecticut. I received 56 timely submissions, of which 53 were correct—good for a 95 percent solve rate. Nice job, everyone!

Last week’s Fiddler was about March Madness, i.e., the NCAA’s men’s and women’s basketball tournaments. These single-elimination tournament brackets consist of 64 teams spread across four regions, each with teams seeded 1 through 16. (In recent years, additional teams beyond the 64 have been added, but that wasn’t relevant for the puzzle.)

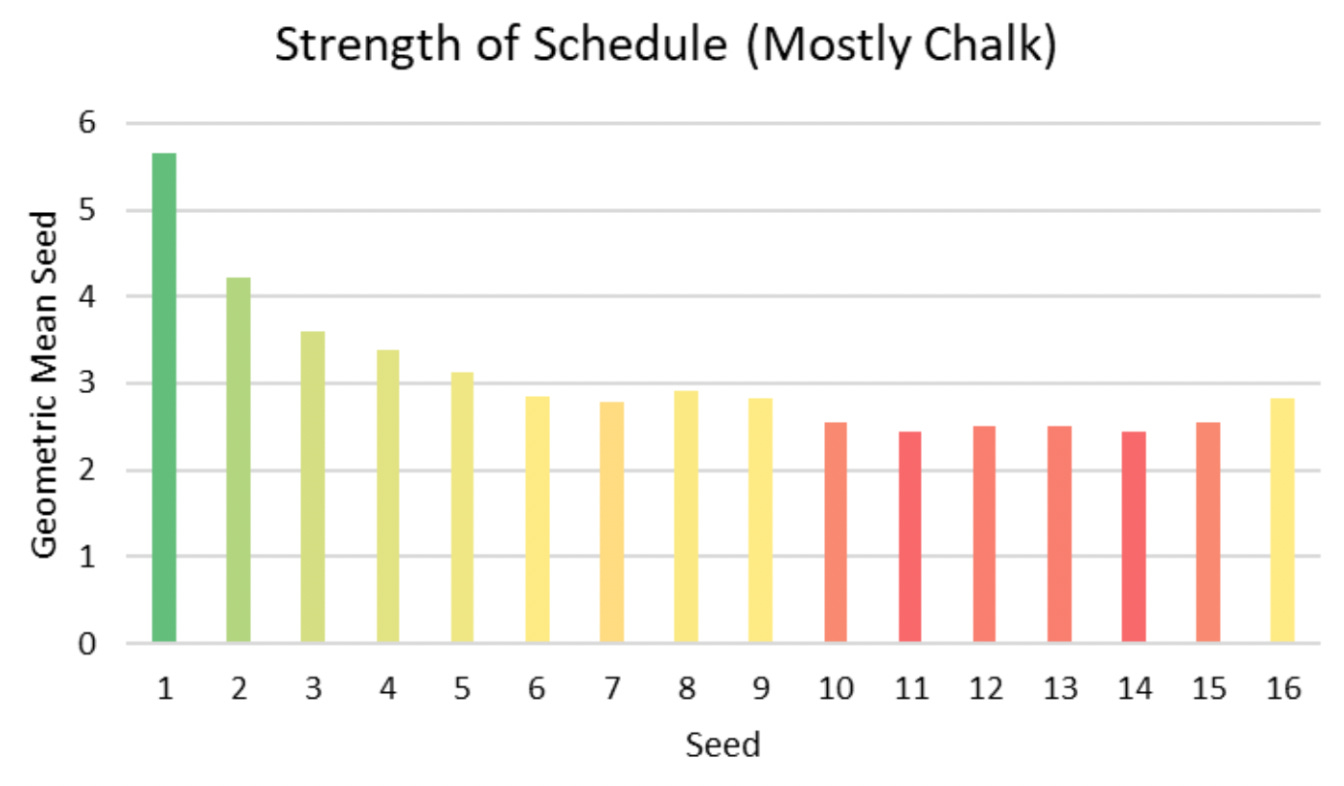
One way to evaluate a team’s strength of schedule within the region was to compute the geometric mean of the strongest opponents a team could face in various rounds.

For example, the 1-seed faced the 16-seed in the first round, then (potentially) the 8-seed in the second round, then (potentially) the 4-seed in the third round, and finally (potentially) the 2-seed in the fourth round. The geometric mean of these opponents was the fourth root (since there were four opponents) of 16 · 8 · 4 · 2, or approximately 5.66. In this computation, we used the 8-seed rather than the 9-seed because 8 was less than 9, we used the 4 seed rather than the 5-seed, 12-seed, or 13-seed because 4 was less than 5, 12, and 13, and so on. The tougher a team’s strength of schedule, the lower this geometric mean.

Of the 16 teams in the region, which two seeds had the toughest strengths of schedule?

Before proceeding, you had to know the precise structure of how various seeds faced each other in the tournament. The key to this structure was that, in any given round of the tournament, the 1-seed (if it hadn’t been eliminated) faced the bottommost seed (if it, too, hadn't been eliminated), the 2-seed faced the second-to-bottom seed, and so on. Here was the resulting bracket for the region:

The bracket itself contained some fascinating structure. One feature was that, should the stronger team (i.e., the team with the lower seed) always win, the sum of opposing seeds in each round was the same up and down the bracket: 17 for the first round, 9 for the second, 5 for the third, and 3 for the last round. Moreover, these values were each one more than decreasing powers of 2.

Right off the bat, you knew that the top eight seeds couldn’t have had the toughest strengths of schedule. Why? Because after the first round, they and their higher-seeded first-round opponents had identical strengths of schedule. But in the first round, their higher-seeded opponents had the more challenging task of facing them. For example, the 1-seed and the 16-seed had identical schedules after the first round. But while the 1-seed only had to face the measly 16-seed in the first round, the 16-seed had the daunting task of knocking off the 1-seed in the first round.

This meant the toughest schedules had to come from the bottom eight seeds, numbered 9-16. But which of these, exactly, had the toughest strength of schedule? Since there were only eight teams to analyze here, most solvers proceeded to analyze them one at a time. (For good measure, we’ll include the top eight seeds here as well.)

• The 1-seed’s strongest potential opponents were the 16-seed, the 8-seed, the 4-seed, and the 2-seed. The 1-seed’s strength of schedule was the fourth root of 16 · 8 · 4 · 2, or about 5.66.

• The 2-seed’s strongest potential opponents were the 15-seed, the 7-seed, the 3-seed, and the 1-seed. The 2-seed’s strength of schedule was the fourth root of 15 · 7 · 3 · 1, or about 4.21.

• The 3-seed’s strongest potential opponents were the 14-seed, the 6-seed, the 2-seed, and the 1-seed. The 3-seed’s strength of schedule was the fourth root of 14 · 6 · 2 · 1, or about 3.60.

• The 4-seed’s strongest potential opponents were the 13-seed, the 5-seed, the 1-seed, and the 2-seed. The 4-seed’s strength of schedule was the fourth root of 13 · 5 · 1 · 2, or about 3.38.

• The 5-seed’s strongest potential opponents were the 12-seed, the 4-seed, the 1-seed, and the 2-seed. The 5-seed’s strength of schedule was the fourth root of 12 · 4 · 1 · 2, or about 3.13.

• The 6-seed’s strongest potential opponents were the 11-seed, the 3-seed, the 2-seed, and the 1-seed. The 6-seed’s strength of schedule was the fourth root of 11 · 3 · 2 · 1, or about 2.85.

• The 7-seed’s strongest potential opponents were the 10-seed, the 2-seed, the 3-seed, and the 1-seed. The 7-seed’s strength of schedule was the fourth root of 10 · 2 · 3 · 1, or about 2.78.

• The 8-seed’s strongest potential opponents were the 9-seed, the 1-seed, the 4-seed, and the 2-seed. The 8-seed’s strength of schedule was the fourth root of 9 · 1 · 4 · 2, or about 2.91.

• The 9-seed’s strongest potential opponents were the 8-seed, the 1-seed, the 4-seed, and the 2-seed. The 9-seed’s strength of schedule was the fourth root of 8 · 1 · 4 · 2, or about 2.83.

• The 10-seed’s strongest potential opponents were the 7-seed, the 2-seed, the 3-seed, and the 1-seed. The 10-seed’s strength of schedule was the fourth root of 7 · 2 · 3 · 1, or about 2.55.

• The 11-seed’s strongest potential opponents were the 6-seed, the 3-seed, the 2-seed, and the 1-seed. The 11-seed’s strength of schedule was the fourth root of 6 · 3 · 2 · 1, or about 2.45.

• The 12-seed’s strongest potential opponents were the 5-seed, the 4-seed, the 1-seed, and the 2-seed. The 12-seed’s strength of schedule was the fourth root of 5 · 4 · 1 · 2, or about 2.51.

• The 13-seed’s strongest potential opponents were the 4-seed, the 5-seed, the 1-seed, and the 2-seed. The 9-seed’s strength of schedule was the fourth root of 4 · 5 · 1 · 2, or about 2.51.

• The 14-seed’s strongest potential opponents were the 3-seed, the 6-seed, the 2-seed, and the 1-seed. The 9-seed’s strength of schedule was the fourth root of 3 · 6 · 2 · 1, or about 2.45.

• The 15-seed’s strongest potential opponents were the 2-seed, the 7-seed, the 3-seed, and the 1-seed. The 9-seed’s strength of schedule was the fourth root of 2 · 7 · 3 · 1, or about 2.55.

• The 16-seed’s strongest potential opponents were the 1-seed, the 8-seed, the 4-seed, and the 2-seed. The 16-seed’s strength of schedule was the fourth root of 1 · 8 · 4 · 2, or about 2.83.

Whew, that was a lot of computation! Fortunately, solver 🎬 Tom Singer 🎬 presented all this information graphically:

Among the 16 teams, the 11-seed and the 14-seed had the two toughest strengths of schedule, both of which were 2.45.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Emily B Zhang 🎻 from Queens, New York. I received 27 timely submissions, of which 24 were correct—good for an impressive 89 percent solve rate!

Instead of 16 seeded teams in a region, now there were 2^N seeded teams, where N was a very, very large number.

The two seeds with the toughest strengths of schedule had seeds that approached fractional values of 2^N. What were these two fractions?