Can You Survive March Madness?

Which teams have the hardest road to the Final Four? (Hint: It's not the 1-seeds.)

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

March Madness—the NCAA’s men’s and women’s basketball tournaments—is here!

The single-elimination tournament brackets consist of 64 teams spread across four regions, each with teams seeded 1 through 16. (In recent years, additional teams beyond the 64 have been added, but you needn’t worry about these teams for this week’s puzzle.)

Among the 16 teams in a region, you might wonder which team has the toughest schedule. One way to evaluate a team’s strength of schedule within the region is to compute the geometric mean of the strongest opponents a team can face in various rounds.

For example, the 1-seed faces the 16-seed in the first round, then (potentially) the 8-seed in the second round, then (potentially) the 4-seed in the third round, and finally (potentially) the 2-seed in the fourth round. The geometric mean of these opponents is the fourth root (since there are four opponents) of 16 · 8 · 4 · 2, or approximately 5.66. In this computation, we used the 8-seed rather than the 9-seed because 8 is less than 9, we used the 4 seed rather than the 5-seed, 12-seed, or 13-seed because 4 is less than 5, 12, and 13, and so on. The tougher a team’s strength of schedule, the lower this geometric mean.

Of the 16 teams in the region, which two seeds have the toughest strengths of schedule?

Extra Credit

Instead of 16 seeded teams in a region, suppose there are 2^N seeded teams in the region, where N is a very, very large number.

The two seeds with the toughest strengths of schedule have seeds that approach fractional values of 2^N. What are these two fractions?

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a puzzle that broke the internet (or at least my internet) earlier this week. That probably means there’s a decent chance you’ve already seen it. But for those of you who haven’t, Daniel Litt asked a seemingly innocuous question, which I’ll paraphrase spoiler-free below:

Flip a fair coin 100 times. It gives a sequence of heads (H) and tails (T). For each HH in the sequence of flips, Alice gets a point. For each HT, Bob gets a point. For example, for the sequence THHHT, Alice gets 2 points and Bob gets 1 point. Who is most likely to win? That is, who is more likely to have more points after the 100 flips?

I’ve featured coin-flipping problems like these more than once in my time at The Riddler and The Fiddler. First off, the probabilities of encountering HH and HT in two consecutive flips are both 25%. Flipping 100 times means there are 99 consecutive flips, so the expected numbers of HHs and HTs are both 99/4, or 24.75.

But while these expected values are equal, the same isn’t necessarily true for Alice’s and Bob’s respective chances of winning. It might have something to do with the fact that Alice’s points are “clumpier,” meaning she racks up more points among relatively fewer scenarios—and I’ll leave it at that.

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Thomas Stone 🎻 from San Francisco, California. I received 24 timely submissions, of which 9 were correct—good for a 37.5 percent solve rate. Clearly, this sort of open-ended geometric puzzle was tricky. (As you’ll see below, I too missed what was technically the optimal solution.)

Last week, I had a slice of uneaten pizza that I wanted to wrap up in aluminum foil before storing in the fridge. The bad news was that I was all out of foil. The good news was that my unusual neighbor had huge sheets of foil.

For every square inch of foil I borrowed from them, I had to babysit their pet snake an additional minute. I hated snakes, and I wanted to request the bare minimum of foil that I needed.

The slice in question was an equilateral triangle with a side length of 10 inches. I specifically wanted to request the smallest rectangle of foil (by area) such that I could completely cover the slice above and below. I couldn’t fold the pizza, but I was allowed to make as many straight folds in the foil as I wanted, without tearing it.

What was the area of the smallest such rectangle of foil that did the trick?

One way to do this was to inscribe the equilateral triangle in a rectangle. That rectangle represented the foil that went under the pizza, and doubling one of its dimensions gave you another rectangle that you could fold on top of the pizza. Shown below is the smallest such rectangle, which had a length equal to the triangle’s base (10 inches) and a width equal to the triangle’s height (5√3 inches). This rectangle had an area of 50√3 square inches, and doubling that gave you the entire area of the foil, which was 100√3, or about 173.2 square inches.

A fun side quest was finding the largest rectangle by area in which you could inscribe the triangle. That turned out to have an area of 50+25√3 square inches, but that was entirely beside the point.

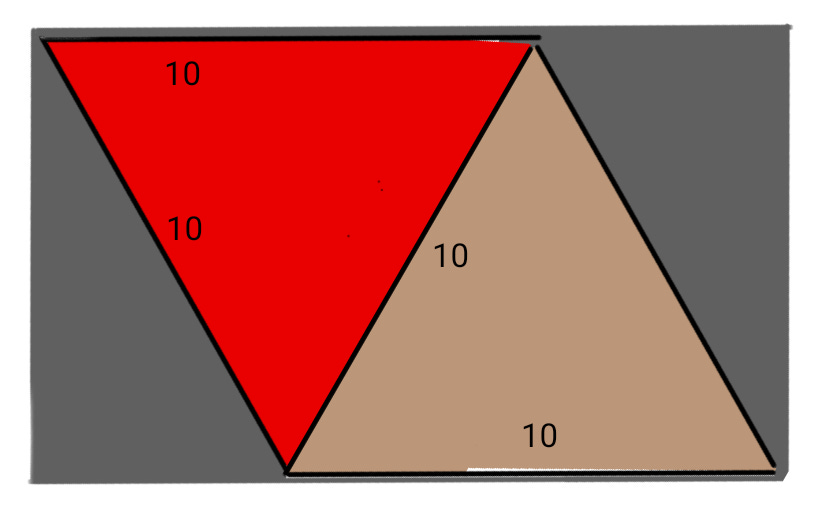
In any case, babysitting a snake for almost three hours didn’t sound too appealing. Fortunately, it was possible to wrap the pizza using even less foil. Lise Andreasen recognized that as long as the foil could contain two adjacent copies of the slice (in which they formed a rhombus, as shown below), you could fold the foil along the common edge of those copies, thereby enclosing the pizza. The smallest rectangle that contained the rhombus had a length of 15 inches and a width of 5√3, which meant its area was 75√3, or about 129.9 square inches. Now, instead of babysitting the snake for three hours, it was a heck of a lot closer to two hours.

But wait! It was possible to use even less foil! Tom Keith positioned the triangle in the rectangle shown below. There were three regions that stuck out from the triangle. The two right triangular regions each covered half the slice, albeit overlapping halves. To fully cover the pizza, the rectangular region had to be thick enough to make it to the slice’s centroid. This rectangular foil had a length of 20/3·√3 inches and a width of 10 inches. Its area was 200/3·√3, or about 115.5 square inches. I was finally under two hours of babysitting the snake!

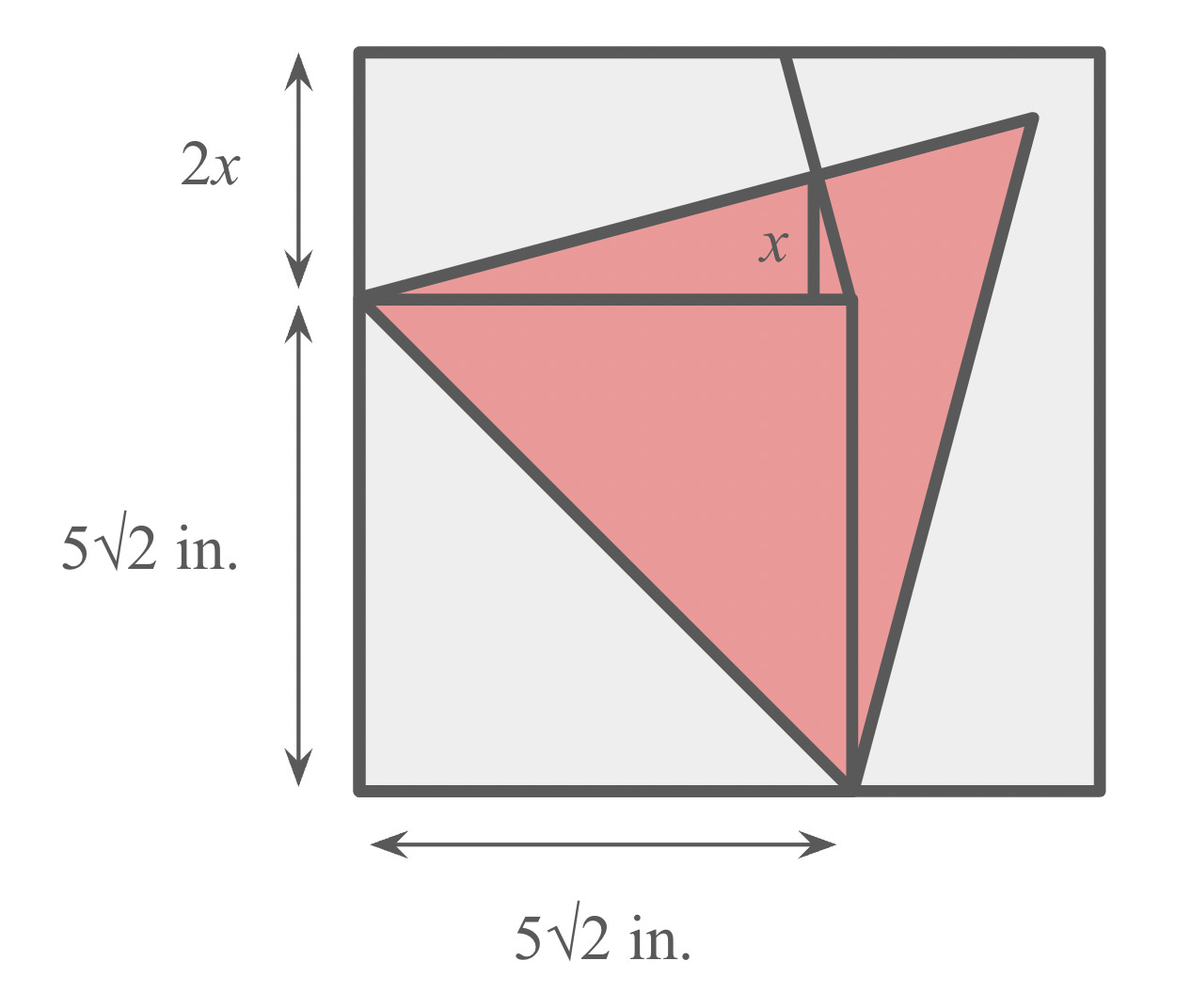
And that still wasn’t the end of it. By rotating the slice so that one edge straddled a corner of a square piece of foil, you could again make three folds along the slice’s three edges such that they all met up at a single point inside the slice, as shown below. That point formed a square with two of the slice’s corners and a corner of the foil; the side length of this square was 5√2.

For the other folds to meet up at that same point, you needed the reflection of that point across the slice’s other two edges to fall on the foil’s edges. With a little trigonometry, the segment labeled x in the above diagram had length 5√2·cos(75°)sin(75°), which meant 2x was 5√2·2cos(75°)sin(75°). Applying a trigonometric double angle formulas let you replace 2cos(75°)sin(75°) with sin(150°), or 1/2. The square foil had side length 5√2 + 2x, which was therefore 7.5√2 inches. The foil’s area was (7.5√2)², or precisely 112.5 square inches, representing yet another improvement.

I’ll be honest with you—I thought 112.5 square inches was the answer. I’m reasonably sure this was the best you could do by making three folds in the foil, one along each edge of the triangular slice. However, the puzzle stated that “I was allowed to make as many straight folds in the foil as I wanted,” which opened the door to even smaller rectangles.

Solvers like Thomas Stone (last week’s winner) and Joe Wetherell (whose diagram appears below) showed that it was possible to achieve an area arbitrarily close to the surface area of the pizza by wrapping a sufficiently thin strip of foil around and around the slice. An equilateral triangle with side length 10 inches has an area of 25√3 square inches. The pizza’s surface was twice that, which was 50√3, or about 86.6 square inches. It was impossible to do any better than that—with any less foil, part of the pizza was guaranteed to be exposed.

I accepted answers of both 112.5 square inches and 50√3 square inches. I fully acknowledge that the latter is technically the “correct” solution, but I wanted to recognize those who offered the former solution, as it was in keeping with the intended spirit of the puzzle.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Joe Wetherell 🎻 from San Diego, California. I received eight timely submissions, of which—you know what? There’s really no point in saying who was “right” or “wrong” here. Every one of the eight came up with a fantastic solution, some of which I’ll highlight here.

Instead of one slice of pizza, I now wanted to wrap two slices of pizza in a single rectangular piece of foil. The two slices were allowed to touch, but they couldn’t overlap in any way (lest the cheese of one slice stick to the other), and their bottoms and tops had to be completely covered by the foil.

Again, what was the area of the smallest such rectangle of foil that would do the trick?