Can You Shut the Box?

Your goal is to flip down six tiles, numbered 1-6. For as many turns as you can, you roll a die and flip down a combination of tiles adding up to the roll. How often can you flip down all six tiles?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

From Seth Cohen comes a game that’ll have you rolling dice and asking, “What’s in the box?”:

In a simplified version of Shut the Box, there are six initially unflipped tiles, numbered 1-6, on the side of a box. You roll a fair, six-sided die, after which you can flip down any combination of unflipped tiles that add to the roll. For example, if you roll a 5, you could flip down the 5, the 1 and the 4, or the 2 and the 3. You proceed until no set of flips is possible (e.g., you rolled a 3 but your only remaining tiles are 2 and 6). To win, you must flip down all six tiles.

Assuming you play with an optimal strategy (i.e., maximizing your chances of winning after any given roll), what is the probability that you’ll win?

This Week’s Extra Credit

Now it’s time for a more standard game of Shut the Box. This time around, you’re rolling two fair, six-sided dice, and there are initially nine unflipped tiles numbered 1-9. To win, you must flip down all nine tiles.

Assuming you play with an optimal strategy, what is the probability that you’ll win?

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a question posted by Grant Sanderson (of 3blue1brown fame).

Here’s a spoiler-free paraphrasing of the question, which apparently has a very surprising (at least to me) answer!

Suppose you independently pick three numbers, x, y, and z, from a uniform distribution between 0 and 1. What is the resulting probability distribution for the quantity (x·y)^z?

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Jasper Ng 🎻 from San Francisco, California. I received 53 timely submissions, of which 15 were correct—good for just a 28 percent solve rate (one of the lowest ever!).

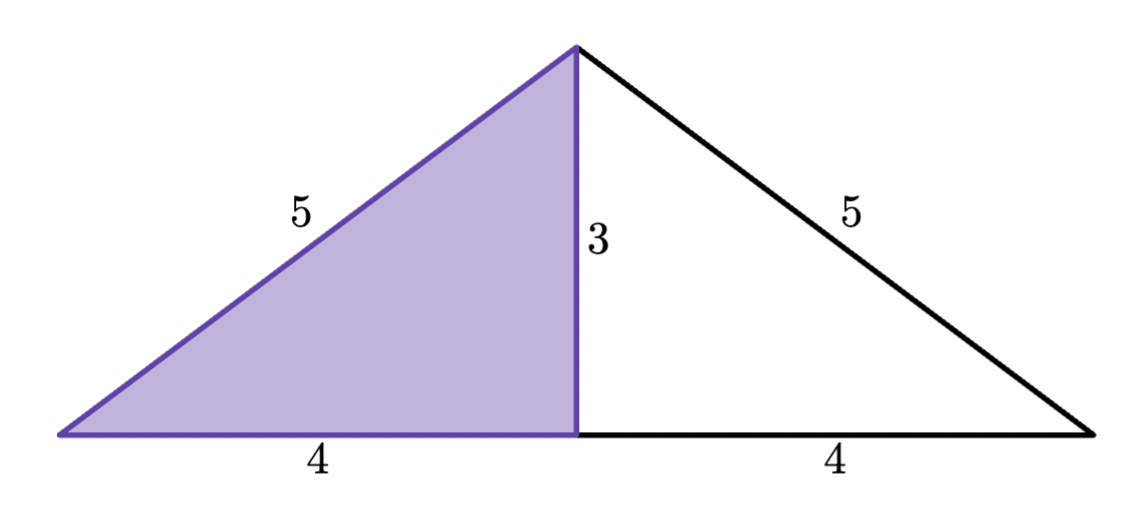
Last week, you saw how, beginning with a 3-4-5 right triangle, you could make an isosceles triangle by appending another triangle to one of its sides. For example, here was how you could make a 5-5-8 isosceles triangle:

Including the one given above, how many distinct ways could you append a triangle to a 3-4-5 right triangle to make an isosceles triangle?

What made this puzzle so tricky was that it was easy to miss one, two, or even three of the isosceles triangles. Many readers found a bunch of them and then assumed they had found them all. Therefore, the key here was organized thinking that allowed you to determine with confidence when you had identified all the triangles.

The isosceles triangle in the image above was generated by extending the leg of length 4 from the original right triangle. Were there any other triangles that could be generated by extending that same leg? Indeed, there was one other (and only one other), the 5-5-√10 triangle shown below:

Next, let’s look at extending the leg of length 3. Because this was the shortest side, there was a way to add a triangle by extending the leg upward, resulting in a 4-4-4√2 triangle:

Extending that leg downward actually resulted in three more isosceles triangles. One that I think just about everyone found was the 5-5-6 triangle that came from reflecting the original triangle across its horizontal leg:

You could also have extended that shortest side by a length of 2, resulting in a 5-5-2√5 isosceles triangle:

The next one was particularly tricky. You could extend the shortest side by a length less than 2, resulting in an isosceles triangle for which 5 was the base. Let’s label that extension x, as in the diagram below:

To solve for x, you had to apply the Pythagorean theorem to the appending triangle: 4² + x² = (x+3)². Since the x² terms canceled, this quadratic equation became a friendlier linear equation, and the solution was x = 7/6. That meant this isosceles triangle was 25/6-25/6-5.

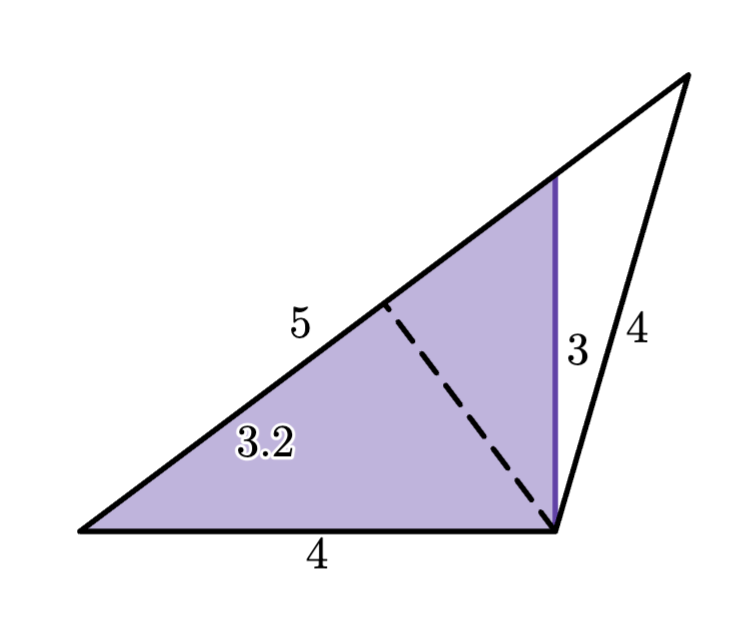
Finally, there was one way to extend the hypotenuse of the original triangle to generate a second side length of 4:

The dashed line in the diagram above shows the isosceles triangle’s altitude, which produced two right triangles that were both similar to the original 3-4-5 triangle. Since these smaller right triangles had hypotenuses of 4, their longer legs had lengths of (4/5)·4, or 3.2. This final isosceles triangle was a 4-4-6.4.

Whew! In the end, there were a whopping seven distinct ways to append a triangle to the original 3-4-5 that resulted in an isosceles triangle. Just for fun, here are all seven plotted at once:

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Emily B Zhang 🎻 from Queens, New York. I received 23 timely submissions, of which 10 were correct—good for a 43 percent solve rate.

Instead of a 3-4-5 triangle, you now had a more general right triangle with legs a and b and hypotenuse c. I told you there were N distinct ways to append a triangle to this a-b-c right triangle to make an isosceles triangle.

What were all the possible values of N?