Can You Find a Matching Pair of Socks (Again)?

You find yourself in a dark room, pulling unpaired socks at random from a drawer, one at a time. Which number sock is most likely to complete your first pair?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

It’s been more than five years since I last ran a sock puzzle. I figured I was due for another one.

I have five distinct pairs of socks in my drawer, none of which is actually paired up. The room is pitch black, so I can’t see the color of any sock I’m pulling out. I reach into my drawer and randomly pull out one of the 10 socks. Then I reach in again and pull out one of the remaining nine. I can keep pulling out one sock at a time, at random, until I decide to stop at some point.

My goal is to stop removing socks as soon as I have a matching pair among those I have drawn. How many socks should I draw to maximize the chances that the last sock I draw results in the first such pair?

This Week’s Extra Credit

Instead of five pairs of socks, I now have N pairs of socks, where N is a very large number. In terms of N, how many socks should I draw to maximize the chances that the last sock I draw results in the first pair?

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing the “Erdős Problems” website, which is cataloging all the “[p]roblems or conjectures posed (either individually or jointly with others) by the great mathematician Paul Erdős.”

There are different monetary prizes associated with each of the problems. Here, I’ll share one of the two problems with a $25 reward:

Find all [positive integers] N such that there is at least one triangle [that] can be cut into N congruent triangles.

Any triangle can be cut into a square number of smaller, congruent triangles. After that, this puzzle gets a lot trickier. Do you have what it takes to solve it and claim your $25 reward (and, you know, eternal glory)?

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Emilie Mitchell 🎻 from Nashville, Tennessee. I received 31 timely submissions, of which 30 were correct—good for a 97 percent solve rate. Great job, everyone!

Last week, you were asked to consider the following array of 25 squares:

You were filling the array with rectangles by repeating the following two steps:

1. Select one of the 12 squares along the outer perimeter that had not yet been selected as part of a rectangle.

2. Form the largest rectangle you could that included the square you just selected and other squares that were not yet part of any such rectangle.

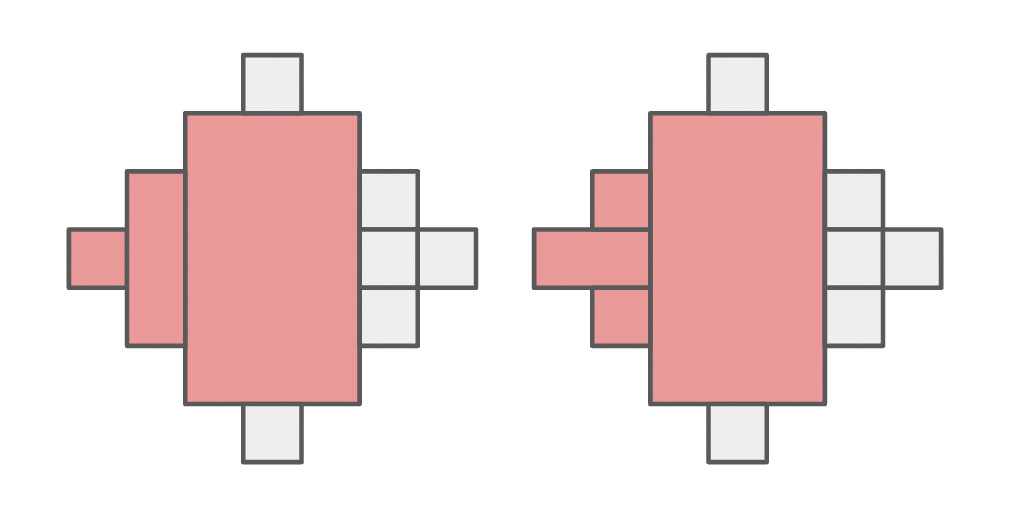
You repeated these steps until every square along the perimeter had been selected. Here were two final states you might have encountered:

How many distinct final states were possible? (Note: States that were rotations or reflections of each other were counted as distinct.)

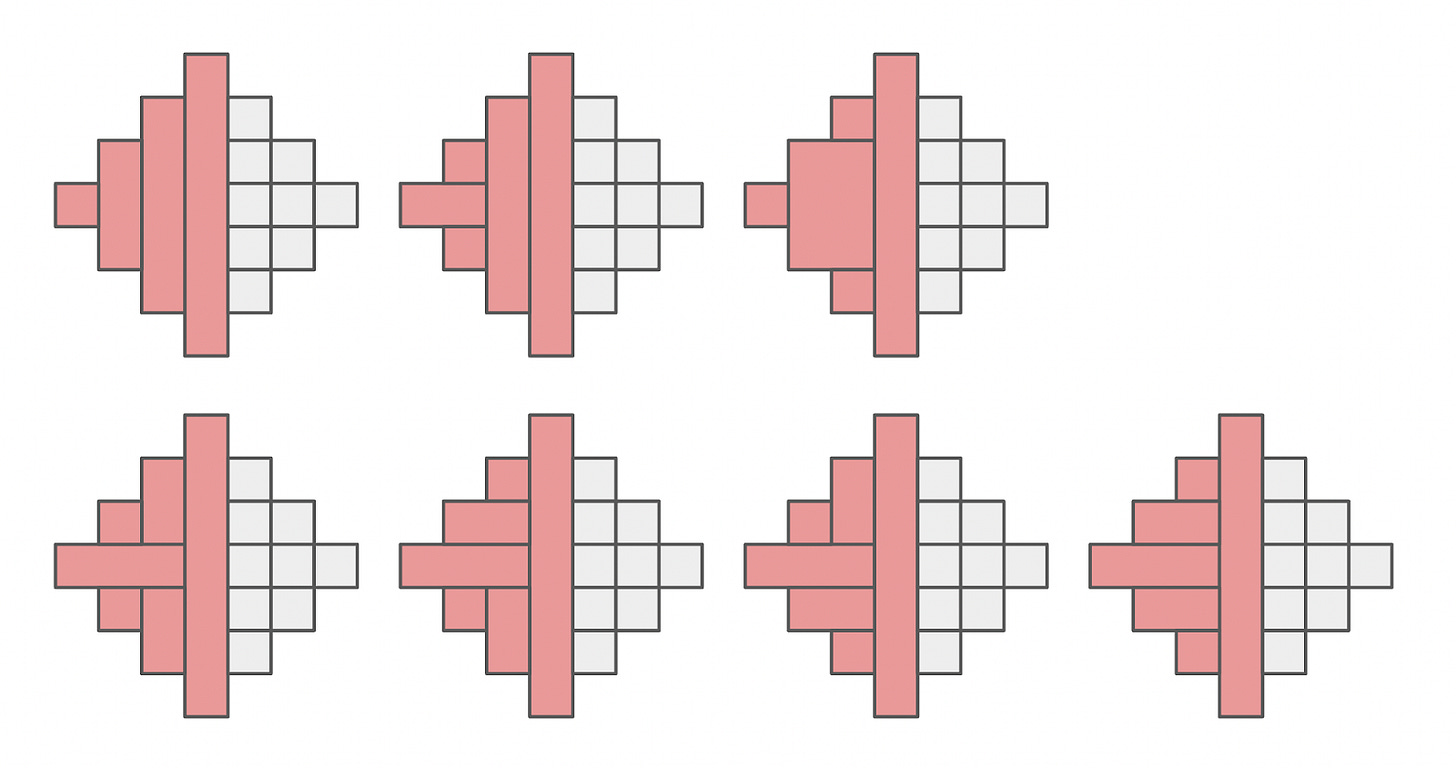
Let’s dive into some casework, shall we? First, suppose the initial square selected was the topmost square, in which case the first rectangle formed was the vertical one that went right down the middle. As shown below, there were then seven distinct ways to form rectangles on the left half of the figure:

Independently, there were also seven ways to form rectangles on the right half of the figure. So when the first rectangle was vertical down the middle, there were 7² ways to combine the seven states on the left with the seven states on the right, for a total of 49 distinct final states.

If the first rectangle had been horizontal across the middle, then there were another 49 distinct final states, all 90 degree rotations from the previous group of 49.

What about when the first rectangle was wider? The two remaining possibilities for the first rectangle were one that was 3 by 5 and one that was 5 by 3. In the case of an initial 3-by-5 rectangle, the top and bottom squares were isolated from the rest of the figure, and there were two ways to turn the remaining squares on the left into rectangles:

Independently, there were two ways to form rectangles among the remaining squares on the right, for a total of 2², or 4, distinct final states.

And when the initial rectangle was 5 by 3, there were another 4 states that were all 90 degree rotations of the aforementioned 4 states.

Altogether, there were 49 + 49 + 4 + 4, or 106 distinct final states.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Brett Kiefer 🎻 from Honolulu, Hawaii. I received 24 timely submissions, of which 16 were correct—good for a 67 percent solve rate.

The array in last week’s Fiddler had four squares along each outer “edge.” For Extra Credit, you had to consider a slightly larger array, with five squares along each edge:

As before, you were filling the array by repeatedly selecting one of the outermost squares and forming a rectangle that included as many “un-rectangled” squares as possible.

How many distinct final states were possible?