How Many Ways Can You Tile the Tilted Square?

If you iteratively fill a tilted array of squares with rectangles, how many distinct final states are possible? For once, the answer cannot be found via OEIS (yet)!

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

From high schooler Taran Knutson comes a puzzle that was originally inspired by the Catalan numbers:

Consider the following array of 25 squares:

You are filling the array with rectangles by repeating the following two steps:

1. Select one of the 12 squares along the outer perimeter that has not yet been selected as part of a rectangle.

2. Form the largest rectangle you can that includes the square you just selected and other squares that are not yet part of any such rectangle.

You repeat these steps until every square along the perimeter has been selected. Here are two final states you might encounter:

How many distinct final states are possible? (Note: States that are rotations or reflections of each other should be counted as distinct.)

This Week’s Extra Credit

The array in this week’s Fiddler had four squares along each outer “edge.” For Extra Credit, consider a slightly larger array, with five squares along each edge:

As before, you are filling the array with rectangles by repeatedly selecting one of the outermost squares and forming a rectangle that includes as many “un-rectangled” squares as possible.

How many distinct final states are possible? (Can you find a general formula for an array with N squares along each outer edge?)

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a puzzle from Tom Bowler that I saw on social media, which I’ll rewrite here (spoiler-free):

Each term in a sequence of positive integers is obtained from the previous term by adding it to its largest digit.

How many successive odd terms can you find in such a sequence?

For example: Starting with 126, the second term would be 126 + 6 = 132. The third term would be 132 + 3 = 135. The fourth term would be 135 + 5 = 140.

For starters, since you’re always adding a digit from 1 to 9, consecutive terms in the sequence can never have the same last digit. After that, you’re on your own!

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Derek Allen 🎻 from Cassopolis, Michigan. I received 49 timely submissions, of which 46 were correct—good for a 94 percent solve rate.

Last week, you wanted to pack four rows of unit circles into a rectangle with a base of length 8. You were considering two strategies for packing:

1. Square packing. In this case, four rows of four circles each were packed in an array of squares.

2. Hexagonal packing. In this case, the bottom row had four circles, and higher rows alternated between having three and four circles.

The following diagrams showed the square packing and hexagonal packing on the left and right, respectively:

While the bases of both rectangles were 8, their heights were as small as possible such that the circles all fit.

Which packing strategy—square or hexagonal—was more efficient for packing these four rows? In other words, which packing resulted in a greater number of circles packed per unit of rectangular area?

Of the two strategies, the square packing was a lot less work to analyze. There were 16 circles packed in a square with side length 8, which meant its area was 8², or 64. Therefore, the packing efficiency (in circles per unit area) was 16/64, or 0.25.

Analyzing the hexagonal packing was a little more work that involved some trigonometry. There were 4+3+4+3, or 14 total circles. As we said, the base of the rectangle was 8. But what was its height?

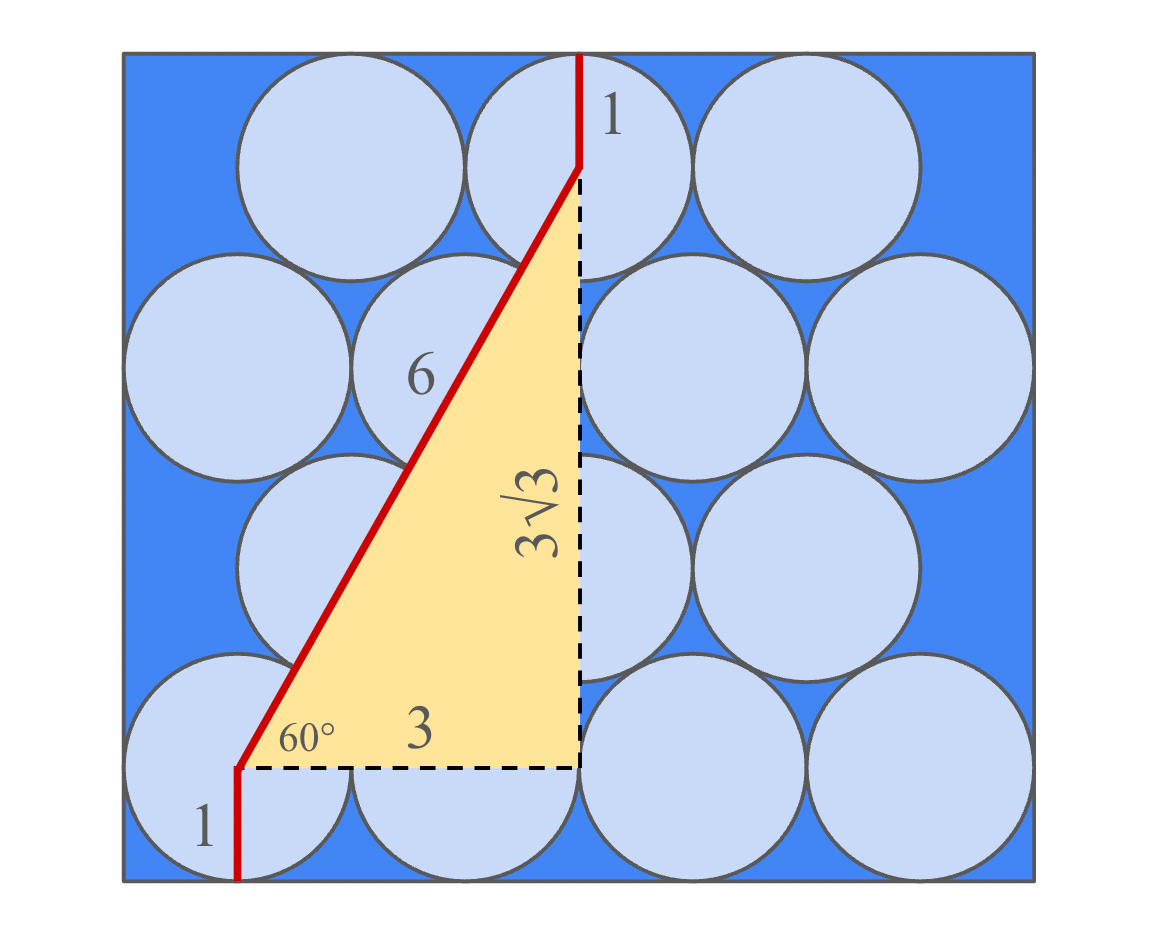
The diagram below shows a path that stretches from the bottom of the rectangle to the top. It’s bookended by radii of length 1. The middle section is the hypotenuse of a 30-60-90 right triangle, whose hypotenuse spanned three diameters, which meant it had length 6. Meanwhile, the horizontal leg had length 3 and the vertical leg had length 3√3, a distance that could have been computed via trigonometry or the Pythagorean theorem.

That meant the height of the rectangle was 1+3√3+1, or 2+3√3, which was approximately 7.196. And the area of the rectangle was 8·(2+3√3), or 16+24√3.

The efficiency of the hexagonal packing (in circles per unit area) was therefore 14/(16+24√3), or approximately 0.243. Since this was less than 0.25, square packing was the more efficient strategy in this instance.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Dennis Okon 🎻 from Falmouth, Massachusetts. I received 35 timely submissions, of which 26 were correct—good for a 74 percent solve rate.

Over large spaces, hexagonal packing of unit circles was more efficient than square packing.

But for Extra Credit, instead of a large space, you had to analyze an 8×k rectangle, where both packing strategies started with four circles on the bottom row of the rectangle. Square packing added additional rows of four circles, one on top of the other, until there was insufficient room at the top of the rectangle. Meanwhile, hexagonal packing added additional rows that alternated between three and four circles, one on top of the other, until there was insufficient room at the top.

I provided diagrams of both packing strategies in an 8×k rectangle (note that the hexagonal-packed rectangle could have had either three or four circles in the top row):

At some point, hexagonal packing was always more efficient than square packing. What was the minimum value of k such that, for all heights greater than or equal to k, hexagonal packing was strictly more efficient than square packing?