Can You Crack the Roman Code?

The code for a vault happens to be written in Roman numerals, which is no problem. But there are no spaces between digits, which is indeed a problem. How many distinct codes are possible?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “Extra Credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

You are breaking into a vault that contains ancient Roman treasure. The vault is locked, and can be opened via a modern-day keypad. The keypad contains three numerical inputs, which are (of course) expressed using Roman numerals: “I,” “II,” and “III.”

It’s a good thing your accomplice was able to steal the numerical key code to the vault. Earlier in the day, they handed you this code on a scroll of paper. Once at the keypad, you remove the scroll from your pocket and unfurl it. It reads: “IIIIIIIIII.” That’s ten vertical marks, without any clear spacing between them.

With some quick mental arithmetic, you realize the combination to unlock the door could be anywhere from four digits long to 10 digits long. (Or is it IV digits to X digits?) How many distinct combinations are possible? If two combinations use the same numbers but in a different order, they are considered distinct.

This Week’s Extra Credit

Having successfully hacked your way through the first keypad, the door opens to reveal a second door with yet another keypad that has eight numerical inputs: “I,” “II,” “III,” “IV,” “V,” “VI,” “VII,” and “VIII.”

You were expecting this, which is why your accomplice had handed you a second scroll of paper. You unfurl this one as well, hoping they remembered to add spaces between the numbers.

No such luck. This paper reads: “IIIVIIIVIIIVIII.” That’s 15 characters in total. How many distinct combinations are possible for this second door?

Making the ⌊Rounds⌉

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing some more fun from X’s Puzzle Corner.

Xavier recently posted a puzzle in which you had to place a point in a disk that maximized how much of the disk’s area was closer to your point than the centroids of three of the disk’s four quadrants. If you don’t mind a spoiler, you can read the solution.

The sequel is a competition in which four strategies for point placement face off at a time, each vying to be close to as much of the disk’s area as possible. To keep things fair, all 24 orderings of competitors will be tested. The tournament among all the submitted strategies is being run imminently!

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Standings

I’m tracking submissions from paid subscribers and compiling a leaderboard, which I’ll reset every quarter. All timely correct solutions to Fiddlers and Extra Credits are worth 1 point each. At the end of each quarter, I’ll 👑 crown 👑 the finest of Fiddlers. This week’s puzzles mark the finale of Q2, so be sure to submit! (If you think you see a mistake in the standings, kindly let me know.)

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻Jason Weisman 🎻 from Wilton, Connecticut. I received 38 timely submissions, of which 7 were correct—good for an 18 percent solve rate, the lowest ever. 🙁

Last week, you were mowing a circular lawn with a radius of 1 unit. You could mow in straight strips that were 1 unit wide.

The smallest number of passes you needed to mow the entire lawn was two. However, instead of minimizing the number of passes, you greedily chose how to orient each pass so it cut as much of the unmowed grass as possible. A pass didn’t have to go through the center of the circle and could be in any direction, but had to be straight and couldn’t bend.

With this “greedy” approach, how many passes would it have taken for you to mow the entire lawn?

Let’s take it one pass at a time. One way to clearly define each pass was with the line, or axis, along the center of the pass. For the first pass, any axis through the center of the circle mowed as much grass as possible.

The original area was 𝜋. How much was actually mowed? The region could be partitioned into two 60-degree sectors and two isosceles triangles, for a total area of 𝜋/3 + √(3)/2. That represented about 61 percent of the total—not bad for a first pass! The remaining area was 𝜋 minus that, or 2𝜋/3 − √(3)/2.

For your second pass, it was tempting to mow one of the two remaining circular segments. Each of them had an area of 𝜋/3 − √(3)/4, precisely 50 percent of the remaining total. However, you could greedily remove a greater area with an axis that again passed through the circle’s center, this time in a perpendicular direction. Here’s what was left after that second pass:

Let’s check that was correct by calculating the percent that was mowed, making sure it was greater than 50 percent. Had it been the first pass, this pass would again have removed 𝜋/3 + √(3)/2. However, the central unit square had already been removed by the first pass. That meant this second pass removed 𝜋/3 + √(3)/2 − 1, which was a whopping 74.3 percent of the remaining area.

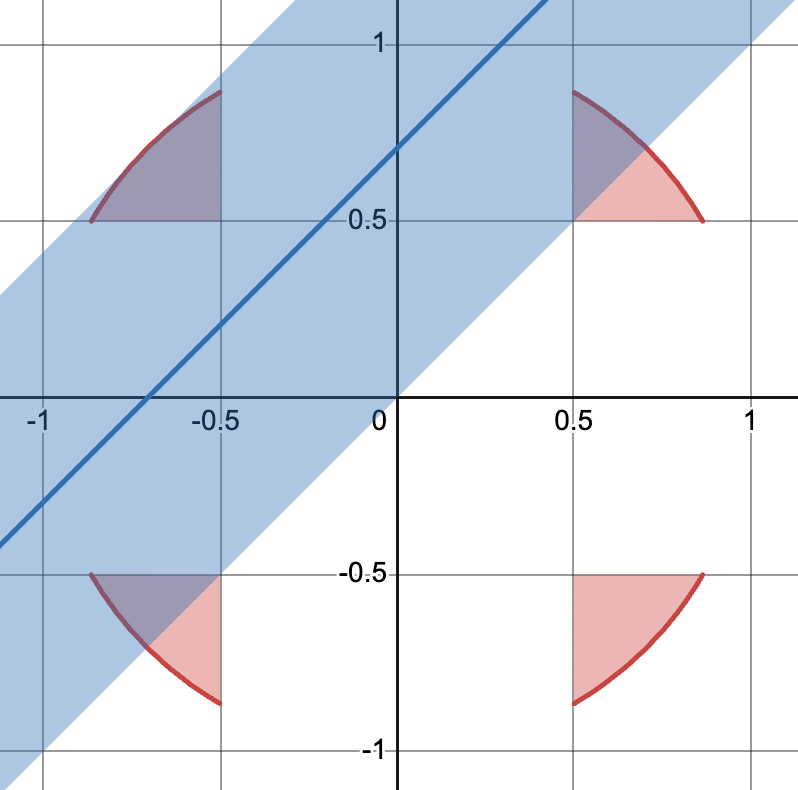
After two passes, you were left with four corners of the original lawn, with each corner separated from the others by a fair bit. Here, it was very tempting to mow two pairs of corners at a time, with axes like x = 0.5 and x = -0.5. In this case, the third pass would have removed 50 percent of the remaining area, while the fourth and final pass removed 100 percent of the area after that. Indeed, the vast majority of readers (74 percent) submitted an answer of four.

But not so fast! Another way to remove 50 percent of the remaining area was with an axis of y = x + 1/√2, as shown below:

But … if we shifted that axis down just a little, we’d only miss a sliver of the top-left patch at first, while removing significant pieces of the bottom-left and top-right patches. The optimal axis turned out to be approximately y = x + 0.65, when the rate at which the top-left patch was being spared equaled the combined rate at which the other two patches were being mowed. Indeed, this pass mowed well over half of the remaining grass.

Removing everything but that sliver in the top left was the greediest option for your fourth pass, while the fifth pass removed the sliver. So the answer was five passes.

(In retrospect, considering the trickiness of this puzzle, I probably should have run this as an Extra Credit. Meanwhile, the actual Extra Credit extended this to three dimensions. Hold on, it’s going to be a wild ride!)

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Jonathan Mooser 🎻 from Mountain View, California. I received 21 timely submissions, of which 17 were correct—good for an 81 percent solve rate.

Instead of mowing a two-dimensional lawn, now you were boring cylinders through a three-dimensional unit sphere. Each cylinder had a diameter of 1 (and a radius of 1/2).

Once again, you were greedily choosing the orientation of your boreholes so that they carved out as much of the remaining sphere as possible with each pass.

With this “greedy” approach, how many passes would it have taken for you to pulverize the entire sphere?