How Many Rides Can You Reserve?

After booking three rides at a theme park, you can reserve one additional ride after each one you complete. On average, how many rides will you complete in a day?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “Extra Credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

I was recently a guest at Disney World, which has a new system called “Lightning Lane” for reserving rides in advance—for a fee, of course.

By purchasing “Lightning Lane Multi Pass,” you can reserve three of the many rides in a park, with each ride occurring at a different hourlong time slot. For simplicity, suppose the park you’re visiting (let’s say it’s Magic Kingdom) has 12 such time slots, from 9 a.m. to 9 p.m. So if you have the 3 p.m. time slot for a ride, then you can skip the “standby lane” and board the much shorter “Lightning Lane” at any point between 3 and 4 p.m. Assume you can complete at most one ride within each hourlong time slot.

Once you have completed the first ride on your Multi Pass, you can reserve a fourth ride at any time slot after your third ride. This way, you always have at most three reservations. Similarly, after you have completed your second ride, you can reserve a fifth ride at any time slot after your fourth, and so on, up until you are assigned a ride at the 8 p.m. (to 9 p.m.) time slot. That will be your final ride of the day.

Magic Kingdom happens to be very busy at the moment, and so each ride is randomly assigned a valid time slot when you request it. The first three rides of the day are equally likely to be in any of the 12 time slots, whereas subsequent rides are equally likely to occur in any slot after your currently latest scheduled ride.

On average, how many rides can you expect to “Lightning Lane” your way through today at Magic Kingdom?

This Week’s Extra Credit

If you’re a Disney aficionado, then you know that week’s Fiddler is in fact an oversimplification of how Lightning Lane actually works. Let’s make things a little more realistic.

This time around, after you complete the first ride on your Multi Pass, you can reserve a fourth ride at any time slot after your first completed ride (rather than after your third ride). Similarly, after you have completed your second ride, you can reserve a fifth ride at any time slot after your second completed ride, and so on, until there are no available time slots remaining.

As before, the first three rides of the day are equally likely to be in any of the 12 time slots, whereas subsequent rides are equally likely to occur in any remaining available slots for the day.

On average, how many rides can you expect to “Lightning Lane” your way through today at Magic Kingdom?

Making the ⌊Rounds⌉

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a puzzle that made its way to me indirectly. Originally posed by James Tanton, a colleague of mine at Amplify, Tom Snarsky, was the one who relayed it to me. Here it is:

The graph of x² + y² = 1 is the set of all points 1 unit from the origin.

Write down an equation (not an inequality) whose graph is the set of all points at a distance different from 1 from the origin!

At first, I was rather confused by this problem. No inequalities? Was I supposed to introduce a third variable? But no, this can indeed be done with just two variables in a single equation. (You just need to see the hole picture.)

Feel free to discuss this puzzle and your approach in the comments below!

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Standings

I’m tracking submissions from paid subscribers and compiling a leaderboard, which I’ll reset every quarter. All timely correct solutions to Fiddlers and Extra Credits are worth 1 point each. At the end of each quarter, I’ll 👑 crown 👑 the finest of Fiddlers. (If you think you see a mistake in the standings, kindly let me know.)

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Seth Cohen 🎻 from Concord, New Hampshire. I received 41 timely submissions, of which 39 were correct—good for a 95 percent solve rate. This was one of those puzzles that was tough, but if you were able to figure out how to go about doing it, then it wasn’t really “tricky” beyond that point.

Last week, you returned to the forest with trees at integer coordinates. This time around, you were at the point (0, 0) on the coordinate plane. There was a tree at each point with nonnegative integer coordinates, such as (5, 6), (0, 7), and (9, 1). The trees were very thin, so that they only obstructed trees that were directly behind them. For example, the tree at (2, 2) was not visible, as it was obscured by the tree at (1, 1).

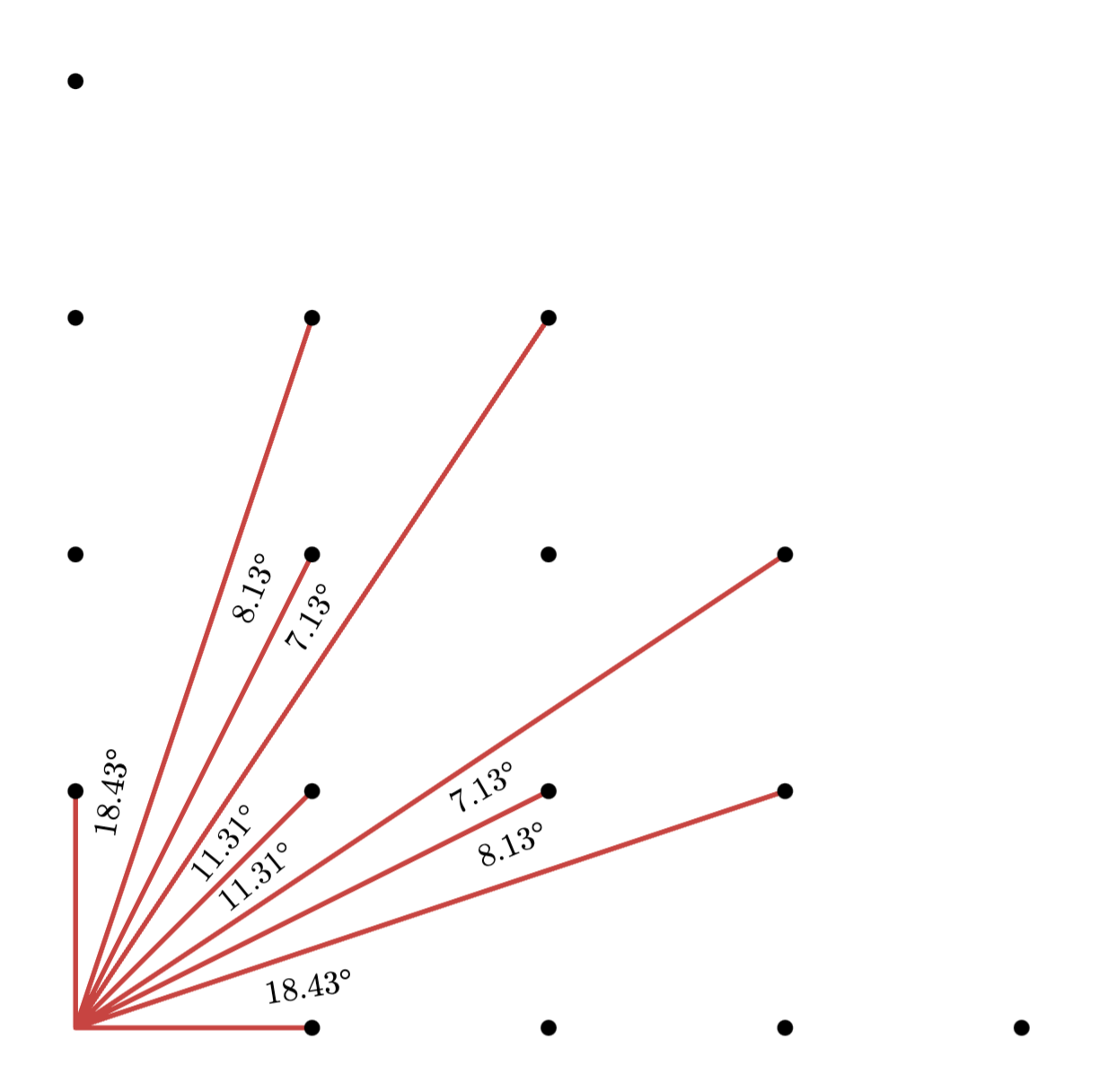
Now, you couldn’t see infinitely far in this forest. Suppose, for example, that the farthest you could see was 4 units. The following diagram showed the trees you could see and the angles between them:

In truth, you could see much farther than 4 units into the forest. You weren’t sure exactly how far you could see, but it was pretty dang far.

As you looked around, you could make out very narrow angular gaps between the trees. The largest gaps were near the positive x-axis and the positive y-axis (similar to the illustrated case above). After those, the next largest pair of gaps were on either side of the tree at (1, 1), 45 degrees up from the x-axis.

You were asked to consider the view between 0 and 45 degrees up from the x-axis. The next largest pair of adjacent gaps in this range were on either side of what angle up from the x-axis? (To be clear, you were not considering the gap just above 0 degrees or the gap just below 45 degrees.)

Let’s suppose that the farthest you could see was some distance d. When d = 4, which was the case diagrammed above, once you removed the angles adjacent to 0 degrees (the x-axis) and 45 degrees, there was only one pair of angles left: those on either side of the point (2, 1). These angles were approximately 8.13 degrees, between (3, 1) and (2, 1), and 7.13 degrees, between (2, 1) and (3, 2).

So when d = 4, the next largest pair of adjacent gaps were on either side of the tree that was tan^-1(1/2), or about 26.565 degrees, up from the x-axis. But what about greater values of d?

Solver 🎬 Ruth 🎬 plotted lines of sight to more trees, revealing the varying sizes of the gaps:

Again, the gaps at 0 and 45 degrees were most prominent. But the gap at 26.565 wasn’t too far behind. The following animation, courtesy of solver 🎬 Eric Widdison 🎬, shows the sizes of the gaps (in degrees) as d increased from 10 to 300. As d increased, the largest gaps continued to occur in pairs on either side of various trees. Moreover, the relative sizes of the gaps remained (surprisingly?) constant. That meant tan^-1(1/2), or about 26.565 degrees, was indeed the answer!

What was going on here? The answer: a lot. In the Extra Credit, I’ll say more about why (2, 1) had the next-largest gaps on either side of it. For now let’s explore the behavior of how these gaps changed as d increased.

But first, it’s worth noting that this puzzle was closely related to Farey sequences. A Farey sequence of order n includes all the fractional values between 0 and 1 whose denominators are at most n. If you respectively treat these fractions’ numerators and denominators as x- and y-coordinates, and then connect the resulting points in order, you generate what’s known as a Farey sunburst. For example, here’s a Farey sunburst of order 6:

Look familiar? One key difference between this puzzle and Farey sunbursts was that your vision in the puzzle had a maximum distance d, defining a circular region on the coordinate plane. Farey sunbursts, on the other hand, occupied a square region.

Let’s consider the point (2, 1), which corresponded to the fraction 1/2 in a Farey sequence. An notable property of Farey sequences is that the terms a/b and c/d are “neighbors” (i.e., they’re adjacent terms in the ordered sequence) if and only if ad − bc = ±1. So for a fraction a/b to be a neighbor of (2, 1), you needed 2a − b = ±1, or a = b/2 ± 1/2. (Note the implication that b had to be an odd integer.) Therefore, such a neighboring point was of the form (b, b/2 ± 1/2). Indeed, in the Farey sunburst of order 6, you could see that the neighbors of (2, 1) were (5, 3) and (5, 2).

Now let’s return to greater values of d. For a neighbor (a, b) of (2, 1) to be approximately d from the origin, the Pythagorean theorem dictated that b² + (b/2 ± 1/2)² ≈ d². For large values of d, this meant (5/4)·b² ≈ d², or b ≈ 2d/√5. For example, when d was 1000, 2·1000/√5 was approximately 894.4, and the neighbors of (2, 1) wound up being (893, 447) and (893, 446). For large values of d, these neighbors could be approximated as ((2/√5)·d, (1/√5)·d±1/2).

We already said the angle to the point (2, 1) was tan^-1(1/2). Meanwhile, the angles to to these two neighbors were tan^-1(1/2±√5/(4·d)). Let’s look at one of these neighbors, say, the one with the greater angle. The gap between this neighbor and (2, 1) was tan^-1(1/2+√5/(4·d)) − tan^-1(1/2). Applying the arctangent difference identity, this equaled tan^-1(√5/(4·d)/(1+(1/2+√5/(4·d))(1/2))). Yikes! Fortunately, for large values of d, this could be simplified to tan^-1(1/(d·√5)). Finally, plugging this into the arctangent Taylor series, to first order this gap was 1/(d·√5) radians.

That was a whole lot of work, but the end result proved that the size of this pair of gaps was inversely proportional to d. As for that √5 term … we’ll get to that shortly!

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Andy Quick 🎻 from Kitchener-Waterloo, Canada. I received 37 timely submissions, of which 26 were correct—good for a 70 percent solve rate.

Last week’s Fiddler asked you to find the largest pair of adjacent gaps between 0 and 45 degrees.

For Extra Credit, the fifth largest pair of adjacent gaps in this range were on either side of what angle up from the x-axis? (Again, you were not considering the gaps just above 0 degrees or the gap just below 45 degrees.)