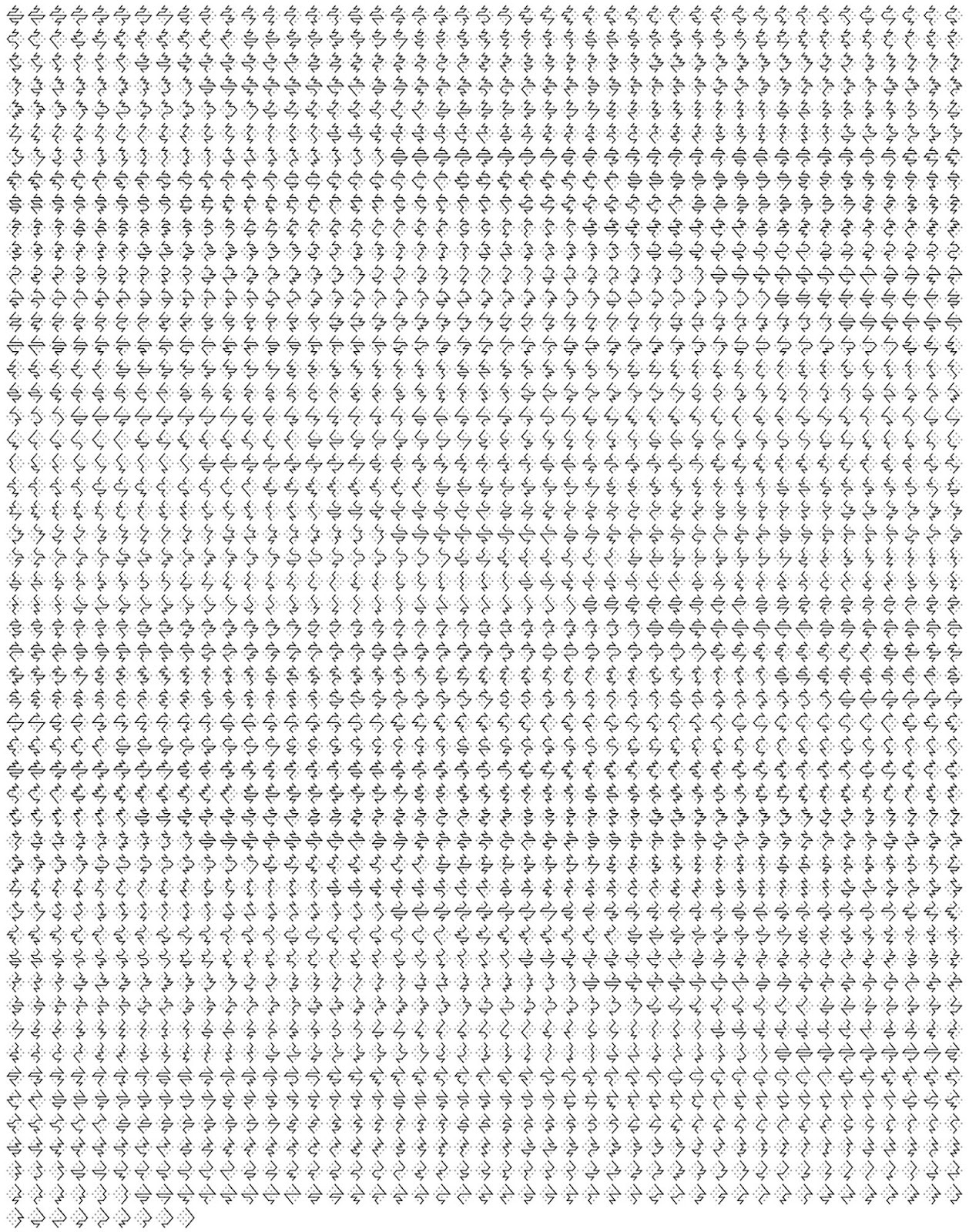How Long Is the River?

Sometimes, everything just lines up. Even the spaces on a massive page of text.

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “Extra Credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

From Seth Cohen comes a puzzle that lines up neatly:

Seth recently came across a phenomenon known as a "river”, where spaces between words diagonally align from one line of text to the next. The following text has an 11-line river in the middle—see if you can spot it!

Before getting to rivers, let’s figure out where spaces are likely to appear in the (fictional) Fiddlish language, which includes only three- and four-letter words. These words are separated by spaces, but there is no other punctuation.

Suppose a line of Fiddlish text is generated such that each next word has a 50 percent chance of being three letters and a 50 percent chance of being four letters. This line also has many, many, many words.

What is the probability that any given character deep into the line is a space?

This Week’s Extra Credit

Now let’s look for some rivers of text!

Fiddlish is written using a monospace font, meaning each character (including spaces) takes up the same amount of horizontal space. As before, lines of text are very, very long, and each next word has a 50 percent chance of being three letters and a 50 percent chance of being four letters. Each line begins with a new word (i.e., words at the end of a line are not hyphenated into the next line).

Suppose the 12th character of a specific line of text is a space. You want to know how long the river down and to the right from this space will be. For example, suppose the 13th character on the next line and the 14th character on the line after that are both spaces, but the 15th character on the very next line is not a space. In this case, the river would have a length of 3. (By this definition, the length of the river is always at least 1.)

On average, how long do you expect the resulting river from the given space (again, the 12th character in its line) to be?

Making the ⌊Rounds⌉

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a new series of puzzles from X's Puzzle Corner. A few weeks back, Xavier posted a puzzle that brought together the classic game Dots and Boxes and polygons. But instead of dots you had the vertices of a regular octagon, and instead of boxes you had triangles formed by edges and diagonals.

The solution for the original puzzle was recently posted. Now, there’s a sequel puzzle that asks how many game configurations are possible. Submissions are due at 11pm this Sunday!

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Standings

I’m tracking submissions from paid subscribers and compiling a leaderboard, which I’ll reset every quarter. All timely correct solutions to Fiddlers and Extra Credits are worth 1 point each. At the end of each quarter, I’ll 👑 crown 👑 the finest of Fiddlers. (If you think you see a mistake in the standings, kindly let me know.)

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Emilie Mitchell 🎻 from Nashville, Tennessee. I received 48 timely submissions, of which 41 were correct—good for an 85 percent solve rate.

Last week, you considered the following figure, which showed 16 points arranged in a rhombus shape and connected to their neighbors by edges. How many distinct paths were there from the top point to the bottom along the edges such that:

• You never visited the same point twice.

• You only moved downward or sideways—never upward.

I suppose you could try tracing all the paths from top to bottom … but it turned out there were quite a few of them—too many (for me, at least) to attempt to count by hand.

A key insight was that a path could be specified row by row with the following information: (1) which branch was taken to enter the row, and (2) which was the last point visited within the row.

Let’s start with the second row. There were two edges between the first and second row. Then, once you were in the row, either of the two points could have been the last point you visited. Since these two decisions (the edge in and the last point to visit) could be made independently, there were 2·2, or 4 paths down through the second row.

Whichever point was your last point to visit in the second row, there were then two edges you could take to reach the third row. And once you were in the third row, you could leave it from any of the three points within it. All told, there were 2·2·2·3, or 24 paths down through the third row.

In leaving the third row, there were two edges you could descend to reach the fourth row. That meant there were 2·2·2·3·2, or 48 ways to reach the fourth row.

At this point, you could have further tallied the number of ways to reach the fifth, sixth, and seventh rows (with the seventh being the bottommost point). Alternatively, you could have turned the bottom half of the figure upside down. That is, every path from the fourth row down to the seventh row could instead be framed as a path from the seventh row up to the fourth row. Like descending from the first row to the fourth row, there were 48 of these paths.

To summarize, there were 48 paths from the topmost point down to the fourth row in the middle, and there were another 48 paths from the fourth row in the middle down to the bottommost point. Any way you picked one of these paths on the top and bottom, there was only one way to connect them within the fourth row. That meant the total number of paths from top to bottom was 48², or 2304. (Based on the symmetry of the figure, you knew from the outset that the answer had to be a square number!)

Solver 🎬 Tom Keith 🎬 plotted all 2304 paths. Not by hand, mind you, but with some computer assistance. Here they were:

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Jonathan Mooser 🎻 from Mountain View, California. I received 29 timely submissions, of which 21 were correct, good for a 72 percent solve rate.

For Extra Credit, you considered the following figure, which showed 30 points arranged in a three-dimensional triangular bipyramid. As before, points were connected to their neighbors by edges. How many distinct paths were there from the top point to the bottom along the edges such that:

• You never visited the same point twice.

• You only moved downward or sideways—never upward.