Can You Survive “The Floor”?

On a popular game show, contestants challenge each other for territory on a square grid. Does your starting position affect your chances of victory?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

From John Hannon comes a puzzle inspired by a television show:

In the game show, The Floor, 100 contestants are assigned to spaces on a 10×10 square grid. Over the course of a season, they compete one-on-one against their immediate neighbors by answering trivia questions. The loser of each duel is eliminated, and the square or squares they control are consigned to the winner.

Let’s consider a slightly simplified version of The Floor with nine contestants on a 3×3 square grid. Each round of the game consists of the following steps:

• One of the remaining contestants is chosen at random. (Note that each contestant is equally likely to be chosen, regardless of how many squares they currently control.)

• The set of eligible opponents for this contestant is anyone whose territory shares a common edge with the contestant. One of these eligible opponents is chosen at random. (Again, all eligible opponents are equally likely to be chosen, regardless of how many squares they control or how many edges they have in common with the opponent.)

• The contestant and their selected opponent have a duel, each with a 50 percent chance of winning. The loser is eliminated, and their territory is added to that of the winner.

These rounds repeat until one contestant remains, and that contestant is the overall winner.

You are a contestant on a new season of this 3×3 version of The Floor. The nine positions on the grid are shown below:

Which position would you choose? That is, which position or positions give you the best chance of being the overall winner?

This Week’s Extra Credit

Again, a new season of the 3×3 version of The Floor (as described above) is about to begin.

What is your probability of winning for each of the nine starting positions?

And for Extra Extra Credit, suppose there are N² positions on an N×N square grid. What is your probability of winning from each of these?

Making the ⌊Rounds⌉

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing some exciting news about a long-standing open puzzle: The moving sofa problem has apparently been solved … maybe? The moving sofa problem can be stated as follows:

What is the largest rigid, two-dimensional shape by area that can fit around a square corner where two hallways of unit width meet?

A semicircular shape with area 𝜋/2 (approximately 1.571) can make it around the corner without issue. And in 1968, John Hammersley found a shape with area 𝜋/2 + 2/𝜋 (approximately 2.207) that can also make it around the corner.

In 1992, Joseph L. Gerver found an even larger shape that can make it around the corner, with an area of approximately 2.2195. The hot news now is that Jineon Baek claims this area is indeed the largest that’s possible. If Baek’s proof is legitimate, then this puzzle has been solved!

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Lasya Kanekal 🎻 from Vista, California. I received 37 timely submissions, of which 34 were correct—good for a 92 percent solve rate.

Last week, you had three particles inside a unit square that all repelled one another. The energy between each pair of particles was 1/r, where r was the distance between them. To be clear, the particles could have been anywhere inside the square or on its perimeter. The total energy of the system was the sum of the three pairwise energies among the particles.

What was the minimum energy of this system, and what arrangement of the particles produced it?

To minimize the energy, you wanted to position the three particles as far away from each as possible. While there were multiple ways to attempt this, as we’ll see, it was pretty clear that all three should have been on the perimeter of the square. If any particle wasn’t on the perimeter, you could have moved it farther away from the other two until it reached the perimeter.

Now, when it comes to optimization problems in which you’re minimizing (or maximizing) something based on a geometrical arrangement, such arrangements tend to be symmetrical. Here, there were several rather symmetrical arrangements worth exploring.

The most symmetrical arrangement for three particles was an equilateral triangle. It was quite possible to inscribe an equilateral triangle in the square, as shown below:

One particle was in a corner, while the other two were a distance x away from the opposite corner. For the three side lengths to be equal, you needed x² + x² = 1 + (1−x)², a quadratic equation that simplified to x² + 2x − 2 = 0. From the quadratic formula, the solution was x = √3 − 1. That meant each side length was √6 − √2. Therefore, the total energy of this arrangement was 1/(√6 − √2) + 1/(√6 − √2) + 1/(√6 − √2). This simplified to 3/4·(√6 + √2), or approximately 2.898.

But lower energies were possible!

Next up, you could position two particles on adjacent corners and place the third particle at the midpoint of the opposite side, as shown below:

The distance between the two corner particles was 1, since this was a unit square. By the Pythagorean theorem, each of them was also a distance √(1² + 0.5²), or √(5)/2, from the third particle. That meant the total energy of this arrangement was 1 + 2/√5 + 2/√5, or 1 + 4/√5, which was approximately 2.789. That energy was lower than the 2.898 from the equilateral arrangement.

But lower energies were still possible!

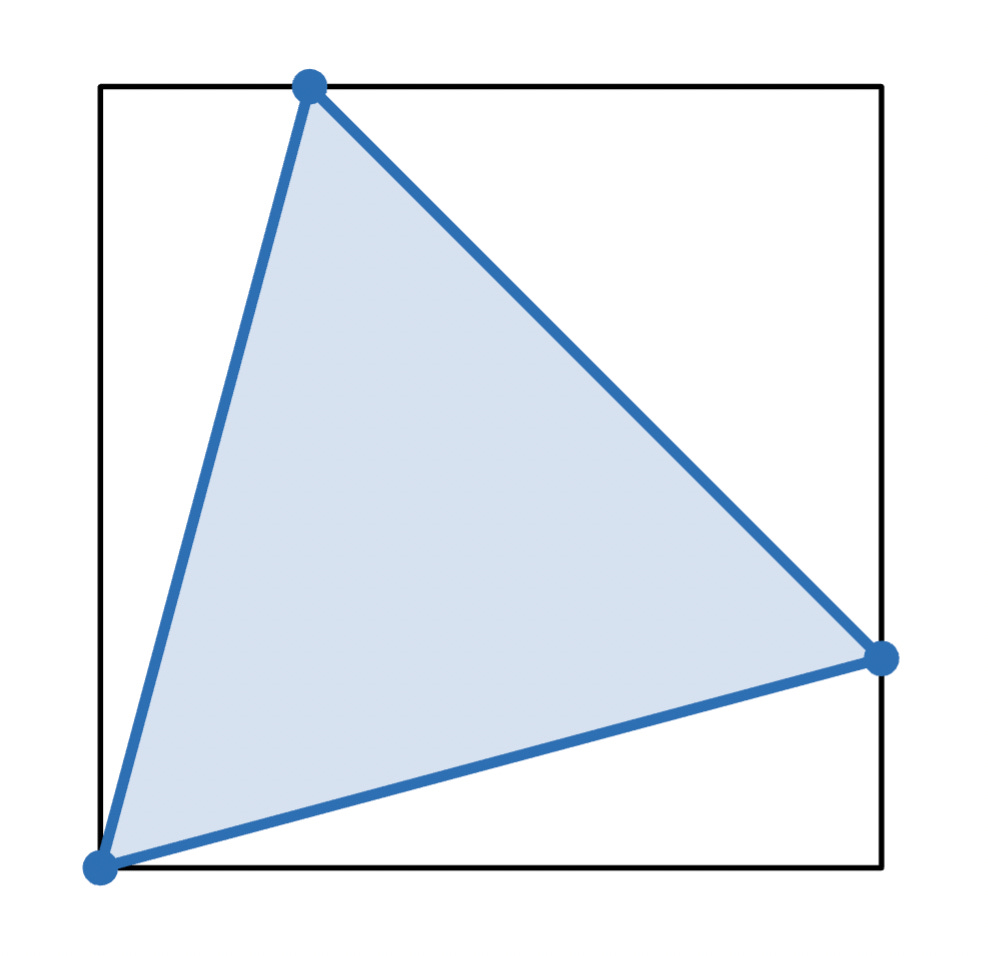
The optimal arrangement turned out to be surprisingly simple. The three particles were located at three corners of the square, as shown below:

One particle was a distance 1 from each of the other two. Those other two were at opposite corners of the square, and therefore a distance √2 apart. The total energy was 1 + 1 + 1/√2, or 2 + 1/√2, which was approximately 2.707.

This right isosceles triangle was the optimal arrangement, which offered the minimum possible energy for the three particles.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Emilie Mitchell 🎻 from Nashville, Tennessee. I received 26 timely submissions, of which 15 were correct—good for a 58 percent solve rate.

Instead of three particles, now you had nine. Again, the energy between each pair of particles was 1/r, where r was the distance between them. The total energy was the sum of the 36 pairwise energies among the particles.

What was the minimum energy of this system, and what arrangement of the particles produced it?