Can You Survive Squid Game (Season 2)?

This time, you’re playing a game of “Mingle.” Contestants split up into groups of equal size. Anyone left over … won’t be in Season 3.

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

In Season 2 of Squid Game, contestants play a game of “Mingle” (spoiler alert!). For each round of this game, the contestants all wait in a common area until a number is called. They must then split up into groups of that number. Any contestants not in a group of the correct number after 30 seconds … well, let’s just say bad things happen to them. For now, we’ll refer to contestants who make it through a round in a group of the correct size as having “survived” the round.

Suppose there are initially N contestants.

In the first round, contestants must form groups of 1. Okay, that’s not too hard; everyone survives. In the second round, contestants must form groups of 2. This continues (with groups of k in round k) until the 38th round, when contestants must form groups of 38.

What is the smallest number N such that there is at least one person who survives all 38 rounds?

This Week’s Extra Credit

There are N contestants about to play Mingle, where N is less than 500. This time, in each round, the number for group size can be anywhere from 1 to 10, with each number equally likely to be called. Also, the numbers called in the rounds are all independent of each other. It appears this version of Mingle will continue until there are no more survivors.

Before the game starts, one of the contestants, Young-il, does some quick computation. He says to his companion, Gi-hun: “Oh no, it’s too bad we only have N people.” (Of course, Young-il doesn’t actually say “N,” but rather the number that N represents.)

Young-il continues: “If we had started with N+1 people instead, I’d expect the game to last about 10 additional rounds, on average, than I’d expect from starting with N people.”

What is the value of N?

Making the ⌊Rounds⌉

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a question that was sent my way by reader Bernardo Recamán. It resembled the New Year’s puzzles I ran a few weeks ago. I’ll paraphrase it spoiler-free here:

A number is said to be “handsome” if it can be written as the sum of positive integers that collectively use each of the 10 digits exactly once. For example, 270 is handsome, because it can be written as 98 + 76 + 54 + 32 + 10.

Is 2025 handsome? And, if so, how handsome is it? That is, in how many distinct ways can it be handsomely partitioned?

Feel free to discuss this puzzle and your approach in the comments below.

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Standings

As I announced last week, I’ll be tracking submissions from paid subscribers and compiling a leaderboard, which I’ll reset every quarter. All timely correct solutions to Fiddlers and Extra Credits will be worth 1 point each. At the end of each quarter, I’ll 👑 crown 👑 the finest of Fiddlers. If you think you see a mistake in the standings, kindly let me know.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Adam DeBruler 🎻 from Atlanta, Georgia. I received 33 timely submissions, of which 14 were correct—good for a 42 percent solve rate, and a bumpy start to the new year.

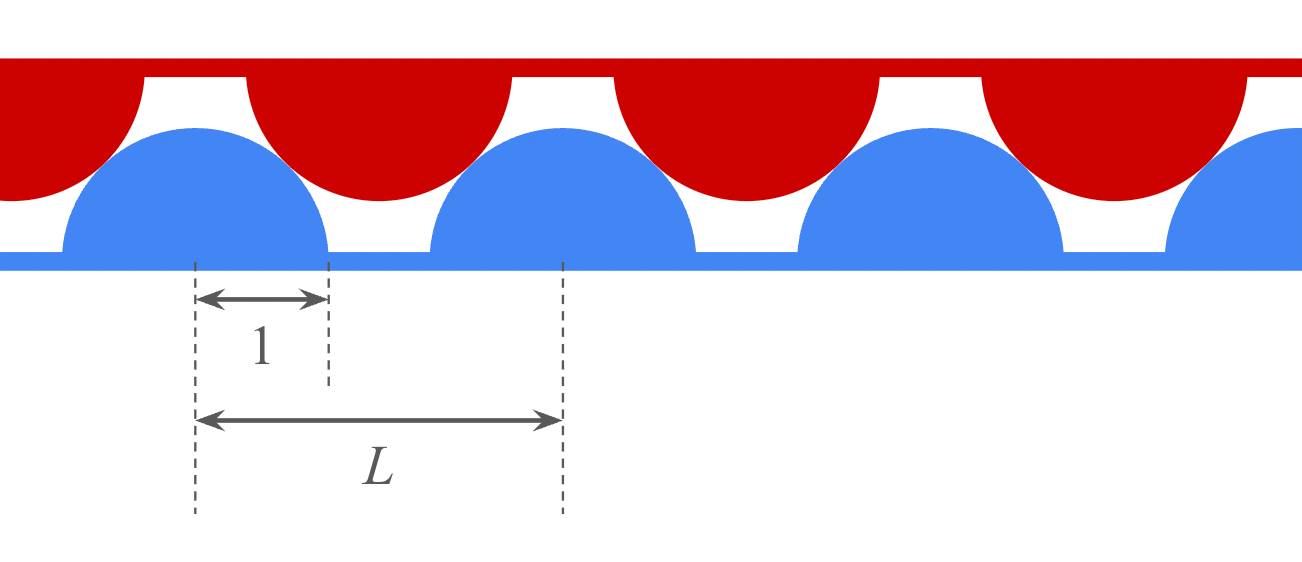
Last week, you considered two large planar sheets that had parallel semi-cylindrical ridges with radius 1. Neighboring ridges were separated by a distance L ≥ 2. The sheets were placed so that the ridges extruded toward each other, and so that the sheets couldn’t shift relative to each other in the horizontal direction, as shown in the cross-section below:

Which value of L (again, that was the spacing between ridges) maximized the empty space between the sheets?

To be clear, you were maximizing the volume of empty space per unit area of one flat sheet. In the cross-section shown above, that was equivalent to maximizing the area of empty space per unit length of one flat sheet.

Let’s start by looking at the two extreme cases: when L was a minimum of 2, and when L was large enough for the two sheets to be a distance 1 apart. When L was 2, the ridges were adjacent to each other, as shown below:

The vertical separation between the sheets was √3. To find the area of empty space in the cross-section, you could analyze a 2-by-√3 rectangular region that repeated. Each such region contained one semicircle and two quarter-circles, for a total of one circle with area 𝜋. That meant the empty area within the rectangle was 2√3-𝜋, or about 0.3225. Since this region had a length of 2, the empty area per unit length was half as much, or about 0.16125.

When the ridges were a distance 2√3 apart, the sheets were separated by the smallest possible distance of 1, as shown below:

In this case, you could analyze a repeating rectangle that was 2√3-by-1. As before, this contained one whole circle with area 𝜋, which meant the empty area within the rectangle was once again 2√3−𝜋. However, the region now had a greater length, 2√3. That meant the empty area per unit length was even lower, about 0.0931.

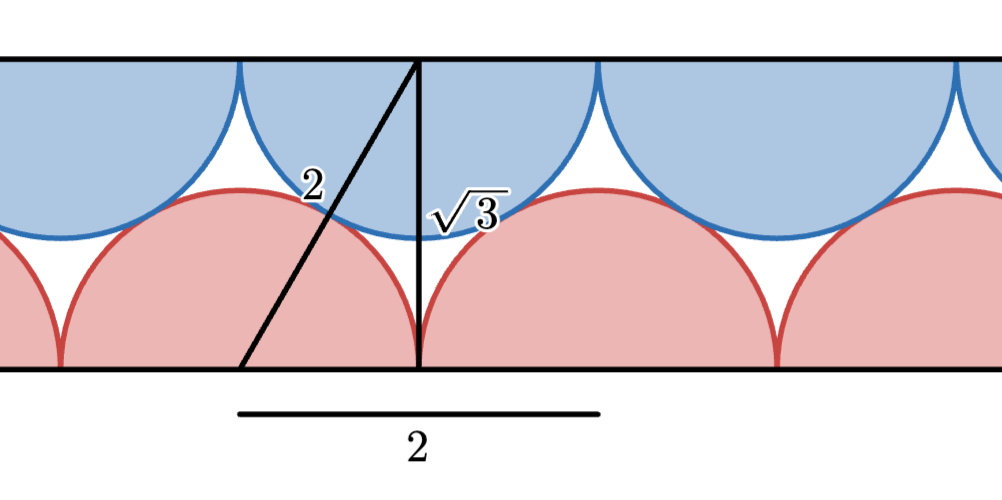
The empty space per unit length (in the cross-section) was maximized when the spacing L was somewhere between 2 and 2√3. A good strategy for determining this maximum was to find an explicit formula for the empty space in terms of L. You could find the vertical separation between the sheets using the right triangle shown below:

By the Pythagorean theorem, the separation was h = √(4−L²/4). To find the empty space, you could consider a repeating rectangle that was L-by-h. As ever, this contained one whole circle, so the empty space was L·h−𝜋, or L·√4−L²/4)−𝜋. Since this region had a length L, the empty space per unit length was √(4−L²/4)−𝜋/L. This was precisely the formula you were looking to maximize. Here’s a graph of it:

You could approximate the maximum of this graph by inspection, or you could find it exactly using calculus. The maximum area per unit length was roughly 0.31264, when L was about 2.6581. I marked any response between 2.65 and 2.66 (inclusive) as correct.

This puzzle tripped up quite a few readers, who maximized the fraction of the interstitial space between the sheets that was empty, rather than the interstitial area per unit length. This gave a different optimal spacing of 2√2, or about 2.828, which was (unfortunately) not what the puzzle was asking for.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Chris Payne 🎻 from Arlington, Virginia. I received 11 timely submissions, of which 6 were correct—good for a 55 percent solve rate.

Instead of cylindrical ridges, now the sheets had any number (greater than zero) of hemispherical deformations with radius 1 that extruded toward each other. This time, the sheets didn’t have to be the same as each other.

As before, the distance between the centers of any two deformations on the same sheet had to be at least 2. What was the minimum empty space, again expressed as volume per unit area of one flat sheet?