Can You Set a Winning Baseball Lineup?

Hopefully you can do better than those woeful New York teams.

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

You are the manager for the New York Frets, a baseball team that has woefully underperformed this season. In an effort to right the ship, you are tinkering with the batting order.

Eight of your nine batters are “pure contact” hitters. One-third of the time, each of them gets a single, advancing any runners already on base by exactly one base. (Your team is very slow on the base paths. That means no one is fast enough to score from first or second base on a single—only from third). The other two-thirds of the time, they record an out, and no runners advance to the next base.

Your ninth batter is the slugger. One-tenth of the time, he hits a home run. But the remaining nine-tenths of the time, he strikes out.

Your goal is to score as many runs as possible, on average, in the first inning. Where in your lineup (first, second, third, etc.) should you place your home run slugger?

Extra Credit

Instead of scoring as many runs as possible in the first inning, you now want to score as many runs as possible over the course of nine innings. What’s more, instead of just having one home run slugger, you now have two sluggers in your lineup. The other seven batters remain pure contact hitters.

Where in the lineup should you place your two sluggers to maximize the average number of runs scored over nine innings?

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a question inspired by a TikTok from Howie Hua, in which Howie explains that you can compute the average of a set of numbers by averaging the averages of subsets—at least when these subsets are the same size and distinct.

Upon viewing this TikTok, David Butler wondered:

[F]or the natural numbers 1 to 12, how far from the true average of 6.5 can you make an average of averages by choosing groups of different sizes?

For example, if you chose the sets {1, 2, 3, 4, 5, 6, 7, 8, 9} and {10, 11, 12}, their averages would be 5 and 11. The average of these two averages is 8, which is 1.5 greater than the true average of 6.5. If you could have any number of sets (perhaps more than two?), how far from 6.5 can you get the average of averages to be?

And what if, instead of the whole numbers from 1 to 12, you started with the whole numbers from 1 to N? By carefully choosing your sets, how far from (N+1)/2 could you get the average of averages to be? (Spoiler alert: David posted a proof of his solution to this generalized version of the puzzle earlier this week.)

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Patrick McKeen 🎻, from Somerville, Massachusetts. I received 55 timely submissions, of which 44 were correct, good for an 80 percent solve rate. Nice job, everyone!

Last week, you found yourself amidst what appeared to be an infinite grid of perfectly cylindrical trees. You were at the point (0, 0), but there was a tree with a radius of 0.25 units (and diameter 0.5 units) centered at every other point in the plane with integer coordinates.

Of course, you couldn’t actually see infinitely many trees. Most of them were obscured by the trees immediately around you. As you looked around in all directions, how many distinct trees were you able to see?

Before getting to the answer, let’s take a closer look at the trees to the east of your position. You could certainly see the tree centered at (1, 0), which was due east. This tree obstructed your view of all the other trees on the positive x-axis. But what was the easternmost tree you could see with a y-coordinate of 1? Peeking north of the tree at (1, 0) meant looking at an angle equal to sin^-1(0.25) north of east, or about 14.5 degrees counterclockwise from the x-axis. When looking in that direction, the first tree you could see was centered at (3, 1), meaning all the trees with a y-coordinate of 1 and an x-coordinate greater than 3 were obscured by the trees centered at (1, 0) and (3, 1).

Continuing this analysis around for the entire 360-degree view, solver 🎬 John 🎬 from Washington, D.C., generated the following image:

As we already said, you could see the trees centered at (1, 0) and (3, 1). In the first quadrant, you could also see (2, 1), (1, 1), (3, 2), (1, 2), (2, 3), and (1, 3). That was a total of eight trees along the x-axis and in the first quadrant. Thanks to symmetry, the total number of visible trees was four times greater, for a total of 32 trees—the answer to last week’s Fiddler.

Finally, I want to extend an additional Best Picture Award to 🎬 Q P Liu 🎬 for slickly animating the trees in the style of a radar scanner.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Ethan Rubin 🎻, from Rocklin, California. For the Extra Credit, I received 34 timely submissions, 27 of which were correct—a 79 percent solve rate.

Once again, you were located at (0, 0) amidst an infinite grid of cylindrical trees. But this time, the trees were narrower, each with a radius of 0.1 units (and diameter 0.2 units).

When you looked due east, your line of sight was 0.9 units, thanks to the tree centered at (1, 0). But if you looked in other directions, it was possible to see farther away.

How long was your longest line of sight? Assume you were looking level with the ground, so that this was a two-dimensional puzzle (rather than three-dimensional one).

As with last week’s Fiddler, a good place to start was to figure out which trees were even visible. Solver 🎬 Joe Kelley 🎬 did this for all the trees in the first quadrant. Again, thanks to symmetry, this pattern was reflected in the other three quadrants.

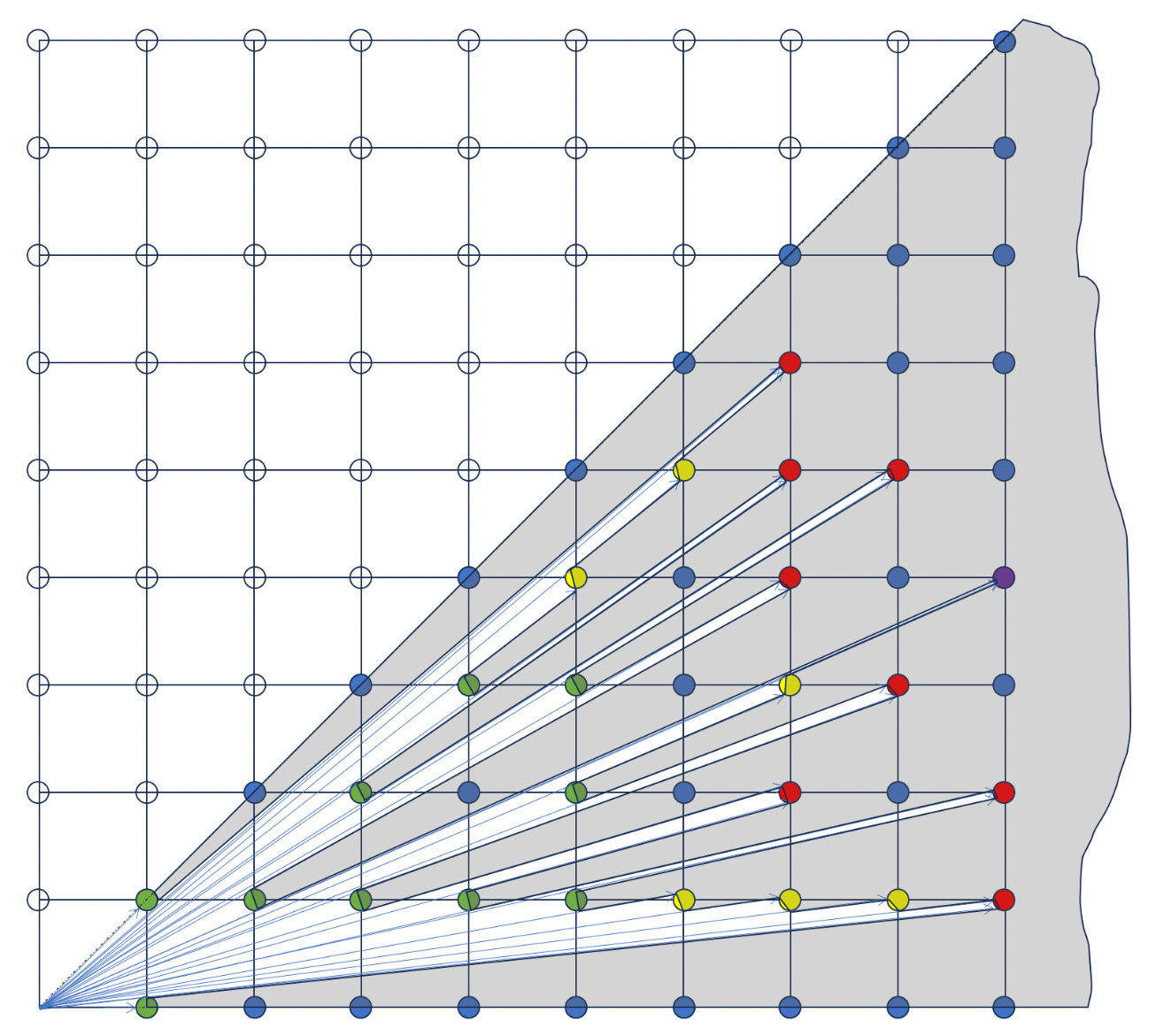
Solver 🎬 Tom Singer 🎬 submitted an equally beautiful image of the bottom-right half of the first quadrant:

In Tom’s diagram, the trees colored in green, yellow, red, and purple were visible from (0, 0). The lone purple tree, centered at (9, 4), was farthest away. The center of the tree was √97, or about 9.85, units from (0, 0). However, √97 wasn’t quite the answer, since the problem was asking for your longest line of sight, whereas this was the distance to the center of the tree. Remember, these trees—like real trees—were opaque.

As it turned out, that tree centered at (9, 4) was barely visible, ostensibly sandwiched between the trees at (7, 3) and (2, 1), whose tangents respectively occurred at angles tan^-1(3/7) + tan^-1(0.1/√58) and tan^-1(1/2) − tan^-1(0.1/√5) counterclockwise from the x-axis. Extending these two tangent lines to the tree at (9, 4) gave you two candidates for the longest line of sight. After a little more algebra, these lengths turned out to be very close: approximately 9.748 units and 9.749 units, the greater of which was 9.749—the solution to last week’s Extra Credit. (For the record, I gave full marks to any solution that rounded to 9.75.)

Solver Laurent Lessard looked at how the number of visible trees and the longest line of sight both grew as the tree radius shrank. At smaller radii, there appeared to be some power laws at work, as shown by Laurent’s log-log plots:

Looking at these graphs, I wonder if the number of visible trees is proportional to the square of the longest line of sight at sufficiently small radii. Maybe with a constant of proportionality like 𝜋?

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.