Can You Ride out the Slow Car Chase?
You have a one-block advantage on your pursuer. But is that enough?
Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.
Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.
Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.
I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.
This Week’s Fiddler
You find yourself engaged in a car chase, but it differs from the movies in one key way: Both you and the car that’s chasing you obey all traffic laws, being sure to stop at any and all red lights.
You’re trying to make it to the city limit, but you’re currently one block ahead of your pursuer. Right now you’re both at a red light. The light turns green at the same time for both of you, at which point both cars begin moving east at a speed of one block per minute.
Every time that you come to an intersection, there’s a 50 percent chance the light is green, in which case you coast right on through. But there’s also a 50 percent chance the light is red, in which case it takes exactly one minute for the light to turn green again. These same probabilities govern your pursuer—at each intersection, they have a 50 percent chance of encountering a green light and a 50 percent chance of encountering a red light and having to wait one minute, entirely independent of whatever you might have encountered at that same intersection.
Including the light at which you are now stopped, there are five traffic lights between you and the city limit, as illustrated below. That means there are six lights for your pursuer.
How likely is it that you’ll make it past the city limit without being caught?
Extra Credit
Now suppose Fiddler City is infinitely large. Once again, you find yourself stopped at a red light, heading due east, with your pursuer one block behind you. Both your light and your pursuer’s light turn green the same instant, and all the other details (i.e., speeds, probabilities, and timings) are the same as before.
On average, how many minutes will it be until you are ultimately caught?
Making the Rounds
There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a neat little problem I found while perusing the sample questions from the Math Kangaroo competition:
Last Week’s Fiddler
Congratulations to the (randomly selected) winner from last week: 🎻 Michael Amati 🎻, from Geneseo, New York. I received 52 timely submissions, of which 27 were correct—good for a 52 percent solve rate. Hey, this was a tough one!
Last week, I was playing the card game Slap with someone who really didn’t like to lose. As a reminder, here are the rules of the game:
Two players are both dealt 26 cards from a standard deck.
From there, they take turns putting down one card at a time. Let’s interchangeably designate the players as “A” and “B.”
If A puts down a jack, then B puts down one card. If it’s a face card, the game continues with A. Otherwise, A wins the round and adds those cards to the bottom of their pile so that the last card played is at the very bottom of the pile.
If A puts down a queen, B has two chances to put down a face card, at which point the game would continue with A. Otherwise, A wins the round and collects the cards.
If A puts down a king, B has three chances to put down a face card, at which point the game would continue with A. Otherwise, A wins the round and collects the cards.
If A puts down an ace, B has four chances to put down a face card, at which point the game would continue with A. Otherwise, A wins the round and collects the cards.
If, at any point, two cards have been played in succession (by different players or the same player) that have the same number or face, then both players can slap the pile of played cards to win the round and collect the cards. (Clarifying note: These two cards had to be played in the same round in order to be slapped.)
Whoever won the previous round plays the first card in the next round.
I really liked this opponent and didn’t want to hurt their feelings. While shuffling, I rigged the deck so that they got a majority of the jacks, a majority of the queens, a majority of the kings, and a majority of the aces.
Nobody likes a cheater, and so my opponent rightfully accused me of rigging the game. In my defense, I said that the probability of one player randomly receiving the majority of each kind of face card was reasonable. What was this probability?
First off, let’s look at just one kind of card, such as the jacks. Now, it was true that any given jack had a 50 percent chance of being in either my pile or my opponent’s. So then, you might (a little naively) think there would be a 1-in-16 chance that my opponent got all four. But thanks to the discrete nature of the problem, that turned out not to be the case.
To find the probability of my opponent having all four jacks, we can take the number of ways to split 52 cards into two 26-card piles such that my opponent’s pile has all four jacks, and divide that by the total number of ways to split 52 cards into two 26-card piles. The denominator was 52 choose 26, or about 496 trillion. To find the numerator, my opponent needed four jacks along with another 22 cards chosen from the remaining 48 non-jacks. That meant the numerator was 48 choose 22, or about 27 trillion. Dividing these very large counts by each other, the probability of my opponent landing all four jacks turned out to be about 5.5 percent—closer to a 1-in-18 chance than the 1-in-16 we computed a moment ago.
Where did this difference come from? Once my opponent had one jack, there was now one fewer spot available for the next jack; two jacks meant two fewer spots, and so on. In other words, the probabilities of my opponent landing successive jacks were not independent of each other, and therefore couldn’t simply be multiplied together.
Now let’s return to the original puzzle. As we already said, the total number of ways to make two piles was 52 choose 26—that would again serve as the denominator for the solution. To find the numerator (i.e., the total number of ways to deal a majority of each kind of face card to my opponent), it helped to break the problem down into five cases, in which my opponent possessed:
All four cards for all four faces (jack, queen, king, ace)
Four cards for three faces, and three cards for the fourth
Four cards for two faces, and three cards for the other two
Four cards for one face, and three cards for the other three
Three cards for all four faces
For case (1), my opponent needed all 16 face cards, plus another 10 from the remaining 36 cards. There were 36 choose 10 ways to choose those cards. (That wasn’t too painful!)
For case (2), my opponent needed 15 face cards, plus another 11 from the remaining 36 cards. There were 36 choose 11 ways to choose those cards, and then you had to multiply this result by 16 to account for which face card I had.
For case (3), my opponent needed 14 face cards, plus another 12 from the remaining 36. This time, you had to multiply 36 choose 12 by 96: six ways to choose two faces that were in my pile, times four possible cards for the first of those faces, times four possible cards for the other face.
For case (4), my opponent needed 13 face cards, plus another 13 from the remaining 36. Here, you had to multiply 36 choose 13 by 256: four ways to choose the three faces in my pile, times four possible cards for the first of those faces, times four possible cards for the second face, times four possible cards for the third face.
Finally, for case (5), my opponent needed 12 cards, plus another 14 from the remaining 36. For this one, you had to multiply 36 choose 14 by 256 yet again, as there were four ways to choose the jack, queen, king, and ace that were in my pile.
Across these five cases, there were a total of about 1.7 trillion ways to make two piles with these conditions. Again, to find the probability, you had to divide this by the aforementioned denominator of 52 choose 26. This gave you the answer of roughly 0.34 percent. A few solvers, like Dan Dima from Bucharest, Romania, expressed the exact value as a fraction: 512,989/150,226,993. This riddle could also have been reasonably interpreted as the probability that either player had a majority of each face card, in which case the answer was double, or about 0.68 percent.
By either interpretation, it was not particularly likely that my opponent should have found themselves with a majority of each face card. Looks like the jig is up!
Last Week’s Extra Credit
Congratulations to the (randomly selected) winner from last week: 🎻 Derek Nagel 🎻, from Savage, Minnesota (a previous winner!). I received 13 timely submissions, of which 7 were correct—good for a 54 percent solve rate.
Last week, it turned out that rigging the deck while shuffling was very hard to do. Instead, I decided to cheat in my opponent’s favor by ensuring my reaction time was slower than theirs at every single slapping opportunity. In other words, I lost every slap.
And so, for Extra Credit, assuming I shuffled and distributed the cards randomly, and that my opponent played the first card in the game, what was my probability of winning?
In all honesty, I wasn’t expecting any analytical solutions here. Sure enough, all I received was numerical, Monte Carlo goodness. The consensus was that my chances of winning without ever slapping were around 4 percent. Thanks to all who attempted this, and especially to those who shared their code. For reference, here are the folks who shared code and agreed the answer was around 4 percent:
🎬 Michael Schubmehl 🎬 went a step further, looking at one’s probability of winning changed as a function of their relative reaction time, as shown below. Oh, the nonlinearity!
Finally, Laurent Lessard generalized the puzzle along a different dimension, exploring one’s chances of winning as the number of players increased.
Want to Submit a Puzzle Idea?
Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.




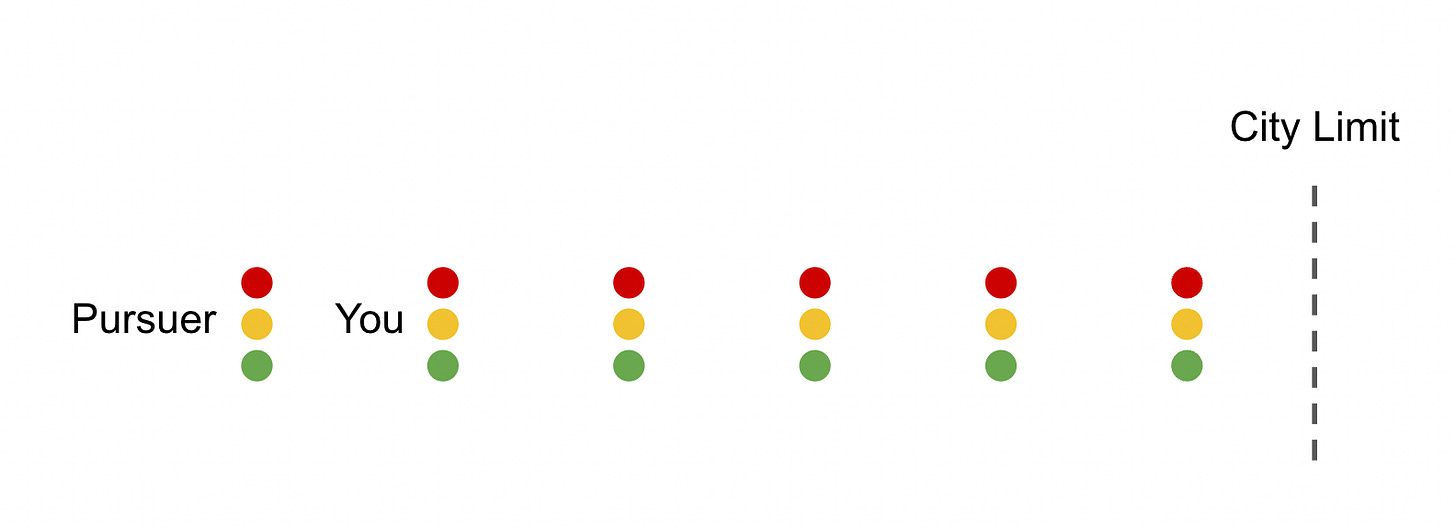


The extra credit for the car catch needs a little clarification of the definition of average. This is a highly skewed result set where some outlying cases can go on indefinitely. So the standard statistical definition of average isn't really very helpful.
For "making the rounds", should we assume that the water level in the tilted tank is at the corner?