Can You Race Across the Chess Board?

How quickly can you move from one corner to the opposite corner, when half the squares slow you down?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

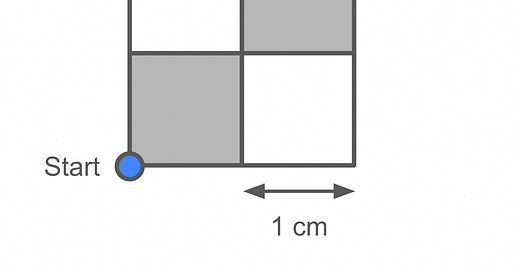
A very tiny Alice (not to be confused with the Alice from last week) is racing across a 2-by-2 chessboard, as shown below, where each smaller square has a side length of 1 cm. Alice starts at the bottom-left corner of the bottom-left black square and is trying to reach the top-right corner of the top-right black square. 

There’s just one catch. Alice moves faster on the white squares than she does on the black squares. Her speed on the white squares is 1 cm per minute (again, she’s very small), while her speed on the black squares is 0.9 cm per minute.

What’s the least amount of time it will take her to reach the finish?

Extra Credit

Instead of a 2-by-2 chessboard, Alice now wants to traverse an 8-by-8 chessboard, as shown below. Again, she’s going from the bottom-left corner of the bottom-left black square to the top-right corner of the top-right black square

As before, her speed on the white squares is 1 cm per minute, while her speed on the black squares is 0.9 cm per minute.

What’s the least amount of time it will take her to reach the finish?

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a puzzle that nerd sniped at least half the folks at my office. The question originated from the design team, but it wasn’t long before the engineering and curriculum teams were all weighing in. It made for a very fun series of threads.

Paraphrasing the original query, it went something like this:

You are designing a table whose headers are slanted by an angle 𝜽, and whose columns have different widths, as shown below.

You want each label to appear the same vertical distance above the bottom line of the header row. Suppose the width of a particular column is p—as is the case for Column 2 in the image above. In terms of p and 𝜽, how much white space should you insert at the beginning of the header text so that it’s always perfectly positioned above the horizontal line?

In other words, how long should the distance indicated by the red brace be, in terms of p and 𝜽?

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Jaimie Zhang 🎻 from Jersey City, New Jersey. I received 103 timely submissions, of which 78 were correct—good for a 76 percent solve rate. That was the third-most solvers in Fiddler history!

Last week, three siblings were at a playground: Alice, Bob, and Carey. Alice, the oldest, got a call from their dad—their pancake dinner was ready! But they wouldn’t get to eat until all three kids were home.

They could each walk home at a different constant speed. Alice could walk home in 10 minutes, Bob could do it in 20, and Carey in 30. Fortunately, any of the kids could carry any of the others on their back without reducing their own walking speed. However, none of them could carry a kid who was, in turn, carrying another kid. They were each able to pick someone up, set someone down, and change direction instantaneously.

What was the fastest they could all get home?

First off, let’s place some bounds on what the answer could have been. What value did you know the answer had to be greater than? Well, there was absolutely no way for all three siblings to get home in less than 10 minutes, since that was the fastest any one of them (i.e., Alice) could get home, regardless of whether she was carrying the other two.

Meanwhile, you also knew the answer had to be less than 30 minutes, since that was the slowest any one of them (i.e., Carey) could get home. Actually, you knew the answer had to be less than 20 minutes, since that’s how long it would have taken if either of Alice or Bob carried (the aptly named) Carey the entire distance.

But it was possible to do even better. Suppose Alice carried Carey all the way home in 10 minutes. Bob was still out here, halfway home. Rather than have Alice twiddle her thumbs, waiting for Bob to make it home, she could have gone out to meet Bob and carried him home faster than he would have made it on his own.

Before we start crunching some numbers, let’s save ourselves a little trouble and suppose that the distance between the playground and home was 60 blocks. (Note that this distance had no effect on the answer. Whatever distance you ascribed, you still got the same result.) Under this assumption, Alice traveled 6 blocks per minute, Bob 3 blocks per minute, and Carey 2 blocks per minute.

So when Alice dropped off Carey and was heading back for Bob, he was still 30 blocks away. With Alice and Bob traveling toward each other a net 9 blocks per minute (6 from Alice and 3 from Bob), they would have reached each after 3 minutes and 20 seconds. From there, Alice would have turned around again and walked another 3 minutes and 20 seconds, this time with Bob on her back. And so, with this itinerary, all three would have been home in 16 minutes and 40 seconds.

Indeed, this was by far the most common incorrect answer I received for this puzzle. (Shocking twist, right?)

How was it possible for the siblings to all make it home even faster? The trick was for Alice to not carry Carey all the way home. Instead, she carried Carey most of the way home and dropped her off. Then, while Carey walked the rest of the way at her slower pace, Alice turned back for Bob, picked him up, and—if all went according to plan—all three showed up in time for pancakes at the same exact moment. After all, if Carey arrived before Alice and Bob, then Alice probably didn’t have to carry Carey quite so far initially. And if Alice and Bob arrived before Carey, then Alice probably should have carried Carey a little farther. This itinerary was nicely diagrammed (not quite to scale) by solver Michael Nolte:

The condition that all three siblings reached home at the same time was the key to solving this puzzle. Suppose Alice dropped Carey off after traveling b blocks (out of 60) in b/6 minutes. That meant Carey had to walk the remaining 60−b blocks at 2 blocks per minute, which took (60−b)/2 minutes.

By the time Alice dropped off Carey, Bob had only traveled b/2 blocks, since he was half as fast as Alice. With Alice and Bob traveling toward each other a net 9 blocks per minute, they reached each other after another b/18 minutes, at a distance 2b/3 from the playground. Alice then carried Bob the remaining (60−2b/3) blocks home at a speed of 6 blocks per minute, which took (60−2b/3)/6 minutes.

Putting this all together, it took b/6 + (60−b)/2 minutes for Carey to arrive home, and it took Alice and Bob b/6 + b/18 + (60−2b/3)/6 minutes. For them all to arrive home as soon as possible, we said these two times had to be equal. Setting the expressions equal, you found that b = 45. Again, this value of 45 was specific to our assumption that the total distance was 60 blocks. But no matter what you assumed this distance was, you found that Alice should have carried Carey 75 percent of the way home initially.

Plugging a value of 45 in for b in either expression for the duration, you found it took the three siblings 15 minutes to arrive home. And that was the fastest they could have done it! Interestingly, half this time (i.e., 7.5 minutes) was spent with Alice carrying Carey with Bob on his own, while the remaining half of the time was spent with Alice snatching up Bob as Carey finished her journey solo.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Joe Wetherell 🎻 from San Diego, California. I received 56 timely submissions, of which only 12 were correct—good (or maybe not so good) for just a 21 percent solve rate. That record low officially made this the trickiest puzzle to have appeared in this column to date!

For Extra Credit, it turned out that Alice, Bob, and Carey had a fourth sibling named Dee, who was with them at the playground. Dee was the slowest, needing 60 minutes to walk home. As before, any kid could carry any other kid, and they wouldn’t start eating until everyone was home.

Once again, what was the fastest they could all get home?