Can You Order the Operations?

I swear, this isn’t about that annoying meme.

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of Zach Wissner-Gross and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

I’m continuing to play Digits (will it ever come out of beta?) from The New York Times. Based on personal experience, I recommend it as a fun way to engage kids with whole number operations. If you’re a fan of Digits, the TV show Countdown, or other similar games, then this week’s Fiddler is for you.

You are writing an expression using the whole numbers 1, 2, 3, 4, and 5, and the operations of addition, subtraction, multiplication, and division. Importantly, you must use each number and operation exactly once. Also, you can use as many parentheses as you would like. No concatenation of the digits is allowed (i.e., you can’t combine 2 and 3 to make the number 23). For example, one such number you could generate is 7, since you can write that as (2÷1)×3+5−4.

What is the largest value you can generate in this way, using the five digits and four operations? (Note: Unlike Digits, fractional values are allowed here.)

Extra Credit

Instead of five numbers and four operations, you now have nine numbers and eight operations. This time around, your expression should include the nine whole numbers 1, 2, 3, 4, 5, 6, 7, 8, and 9, each of which must be used exactly once. And the operations are once again addition, subtraction, multiplication, and division, each of which must be used exactly twice. As before, you have unlimited parentheses, while concatenation is not allowed.

What is the largest value you can generate, using the nine digits and eight operations?

(What if you have the numbers from 1 to 4N+1 and each of the four operations must be used exactly N times?)

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a challenge I saw via Twitter on June 25, 2023, which was to prove (or disprove) the following statement:

At first, the statement might seem too incredible to believe. But with some modular arithmetic, you just might be able to prove it!

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 James Kilfiger 🎻, from East Grinstead, England. For this inaugural Fiddler, I received 70 timely submissions, of which 19 were correct. A 27 percent solve rate—not bad for a first showing.

Last week, it was all about Möbius strips! I started with a strip of paper that was 10 inches long and 1 inch wide. I twisted it once and attached the two 1-inch edges together, forming a Möbius strip. Finally, I drew a dot somewhere along the midline of the strip—that is, the dot was half an inch away from both edges.

I defined the “distance” between any two points on my strip as the shortest path between them—as the ant crawls. By that, I meant that such paths could go over an edge to the other “side” of the strip (“side” in quotes because it’s all really the same side), just as an ant would crawl around the edge of the paper.

There was a point (or points) on the strip that was the farthest distance from my dot. What was this distance?

There was quite a bit of disagreement among readers about the answer here, which was reflected by the relatively low solve rate. I didn’t help matters by initially claiming that there was a unique point that was a maximal distance from the dot, when in fact there were two such points. In any case, this puzzle was quite tricky.

First off, suppose I hadn’t twisted the strip at all, instead creating a ring with two distinct sides. If I made a dot somewhere along the midline of the outside surface, the farthest point would be diametrically opposite along the midline of the inside surface. The shortest path between these two points for an ant would involve crawling around the ring, crossing over the edge between the surfaces a quarter of the way around the ring. By the Pythagorean theorem, the total distance would have been √(5²+1²)—since it was 5 inches around half the circumference and 1 inch in the perpendicular direction to cross over to the other surface—or roughly 5.099 inches. Quite a few readers thought this was the answer. But it was not.

Why? Because of that dang twist. Imagine being an ant who started on the dot, which we’ll call point A. If you crawled 5 inches along the midline in one direction, sure, you’d find yourself at point B, diametrically opposite (in a way) from A. But if you crawled 5 inches along the midline in the other direction, you’d find yourself at point C, again diametrically opposite from A but now on the flip side from B. It was certainly possible to find points that were farther from A.

So if the farthest point on the Möbius strip wasn’t diametrically opposite along the midline, where was it? Many readers picked one of the two points along the edge (rather than the midline) that were diametrically opposite. Either way the ant departed from A, the distance traveled to these points was √(5²+0.5²), or about 5.0249 inches.

But you know what? That wasn’t the answer either. Suppose the ant traveled from A to B, and then went a little farther along the midline, say, by a distance x. If x was sufficiently large, it would eventually make sense for the ant to instead have initially set out in the other direction, toward C, and crawl over the edge along the way. For some value of x, these two distances were equal. And that value of x could be found by setting the distance traveled one way equal to the distance traveled the other way:

\(5+x=\sqrt{\left(5-x\right)^2+1^2}\)

These two expressions were equal when x was 0.05, which meant the point 0.05 inches past B along the midline was at least 5.05 inches from A no matter which way the ant crawled. With a little more work, you could further convince yourself that a point off the midline had to be closer to A, which meant 5.05 inches was indeed the answer.

Still not convinced? Then check out the video in the write-up by solver 🎬 Glenn Horton-Smith 🎬, who propagated a wave out from point A to see which points were the last to be reached. Here are two key moments from that video:

In both images, point A is in the dead center of the rectangle. On the left is when the wave has started propagating outward, and on the right the wave has finally reached those last two points, both on the midline, 5.05 inches in either direction.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Isaac Grosof 🎻, from Pittsburgh, Pennsylvania. For this inaugural Extra Credit, I received 34 timely submissions, all of which were correct. Incredible work, everyone!

For Extra Credit, you started with a prism whose bases were regular N-gons. You twisted it and stretched it into a loop, before finally connecting the two bases to form a “Möbius prism.” The twist was by a random angle, such that the two bases were aligned when they were connected.

For example, if you had started with a square prism (i.e., N = 4), there were four kinds twists that could be applied, all equally likely:

• A one-quarter twist, which resulted in one distinct face

• A two-quarter (or one-half) twist, which resulted in two distinct faces

• A three-quarter twist, which resulted in one distinct face

• A four-quarter (or whole) twist, which resulted in four distinct faces

A randomly twisted square prism would have, on average, (1+2+1+4)/4, or two distinct faces.

Among all whole number values of N less than or equal to 1,000, for which value of N would a randomly twisted regular N-gonal prism have the most distinct faces, on average?

Looking closer at the four cases of the square prism, the number of distinct faces was always the greatest common divisor (or “gcd” – not to be confused with the non-existent “greatest common denominator”) of the number of quarter twists applied and 4. For a one-quarter twist, the number of distinct faces was gcd(1, 4), or 1. For a two-quarter twist, the number of distinct faces was gcd(2, 4) or 2. Similarly, gcd(3, 4) was 1 and gcd(4, 4) was 4. It turned out this connection to the gcd held for every value of N, not just when N = 4.

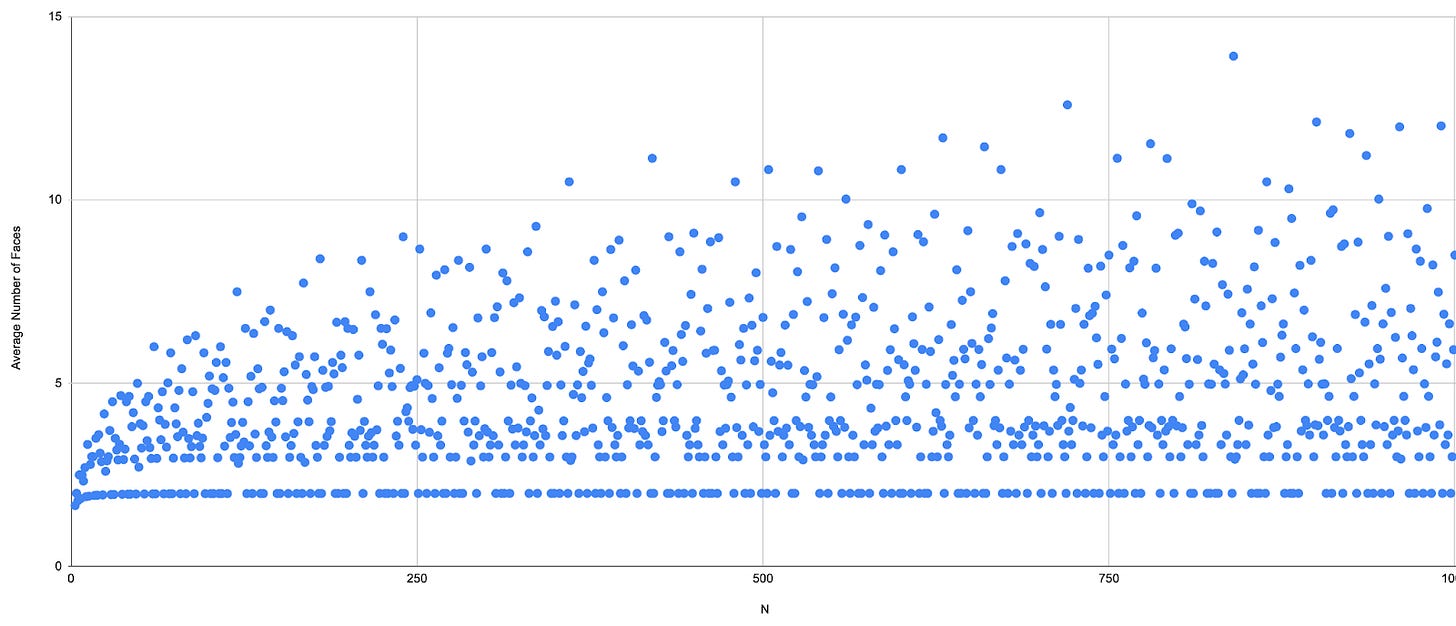
From there, the average number of distinct faces for an N-gonal Möbius prism was the average of the greatest common divisors of N and all the numbers from 1 to N, which could be written mathematically as the function:

\(f(N)=\frac{1}{N}\sum_{k=1}^{N}{\text{gcd}(k,N)}\)

This was a particularly noisy function, but it tended to be greater when N had many factors, meaning it had more numbers with which it shared divisors greater than 1. Solver 🎬 Marion Lara 🎬 graphed this function:

It turned out the maximum among N less than 1,000 was when N was 840. For a randomly twisted 840-gonal prism, the average number of faces was 195/14, or approximately 13.93.

As I always love to see, the puzzling for many readers didn’t end with the solution. A few solvers noted that it wasn’t too surprising that 840 was the answer here, as 840 is what’s called a highly composite number, meaning it has more factors than all the whole numbers less than it. However, not all highly composite numbers were like 840 in that they had greater values of f(N) than the numbers less than them. Meanwhile, solver 🎬 Laurent Lessard 🎬 generated a logarithmic version of the graph of f(N) in an effort to better understand its upper bound, which didn’t quite seem to follow a power law.

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.