Can You Figure the Factorial Numbers?

No, security will not be escorting you out of the math department for playing with this awesome number system.

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

Michael Schubmehl (who won a 🎬 Best Picture Award 🎬 just  two Fiddlers ago) poses a puzzle inspired by a recent xkcd comic:

Number systems like decimal, binary, and hexadecimal each have a fixed number of allowed digits in each place (10, 2, and 16, respectively), while “mixed-radix” systems like the 24-hour clock can have a different number of allowed digits in each place (24 hours, 60 minutes, and 60 seconds, for example). Counting works the same way in all of these systems: When incrementing the rightmost digit causes it to roll from its maximum value back to zero, we “carry” this overflow by incrementing the next digit to the left: 09 increments to 10 in base 10, and 00:00:59 increments to 00:01:00 on the clock.

In the factorial number system (not a prank), the Nth digit from the right has base N, and thus a maximum allowable digit of N−1. As a result, the rightmost digit is always 0 (don’t get me started on “base 1”), the digit to its left can be 0 or 1 (in good old base 2), the next digit can be 0, 1, or 2 (in base 3), and so on. This is called the factorial number system because the place value of the N^th digit is (N−1)!.

Let’s look at an example. Suppose a number is written 103210 in the factorial number system. What is this number in base 10? It’s 1(5!) + 0(4!) + 3(3!) + 2(2!) + 1(1!) + 0(0!), or 143. (Note that the numbers in bold are exactly the digits from the factorial number representation.)

What is the smallest number in the factorial number system that is divisible by the whole numbers from 1 through 5, while also containing all of the digits 0 through 5? (Note that this number can have more than one copy of any given digit.)

You can submit this number using the factorial number system or in base 10.

Extra Credit

This week’s Extra Credit also comes courtesy of Michael Schubmehl:

What is the smallest number in the factorial number system that contains each of the digits 1 through 9 exactly once, and is also divisible by all of the whole numbers from 1 through 9? (Note that this number can contain any amount of zeros.)

This time around, please submit this number using the factorial number system.

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a puzzle from a social media post that recently went viral:

In the post, this was described as an “insanely hard” interview problem. I can’t speak to whether it really was an interview problem, but the rest of that description checks out. Flipping the x- and y-axes might help you clean up your algebra a little, but there’s no avoiding a messy (and fun) time.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Jacob 🎻, from Hamilton, New Zealand. I received 66 timely submissions, of which 53 were correct, good for an 80 percent solve rate.

Last week, you were playing a game of pinball that included four lanes, each of which was initially unlit. Every time you flipped the pinball, it passed through exactly one of the four lanes (chosen at random) and toggled that lane’s state. So if that lane was unlit, it became lit after the ball passed through. But if the lane was lit, it became unlit after the ball passed through.

On average, how many times did you have to flip the pinball until all four lanes were lit?

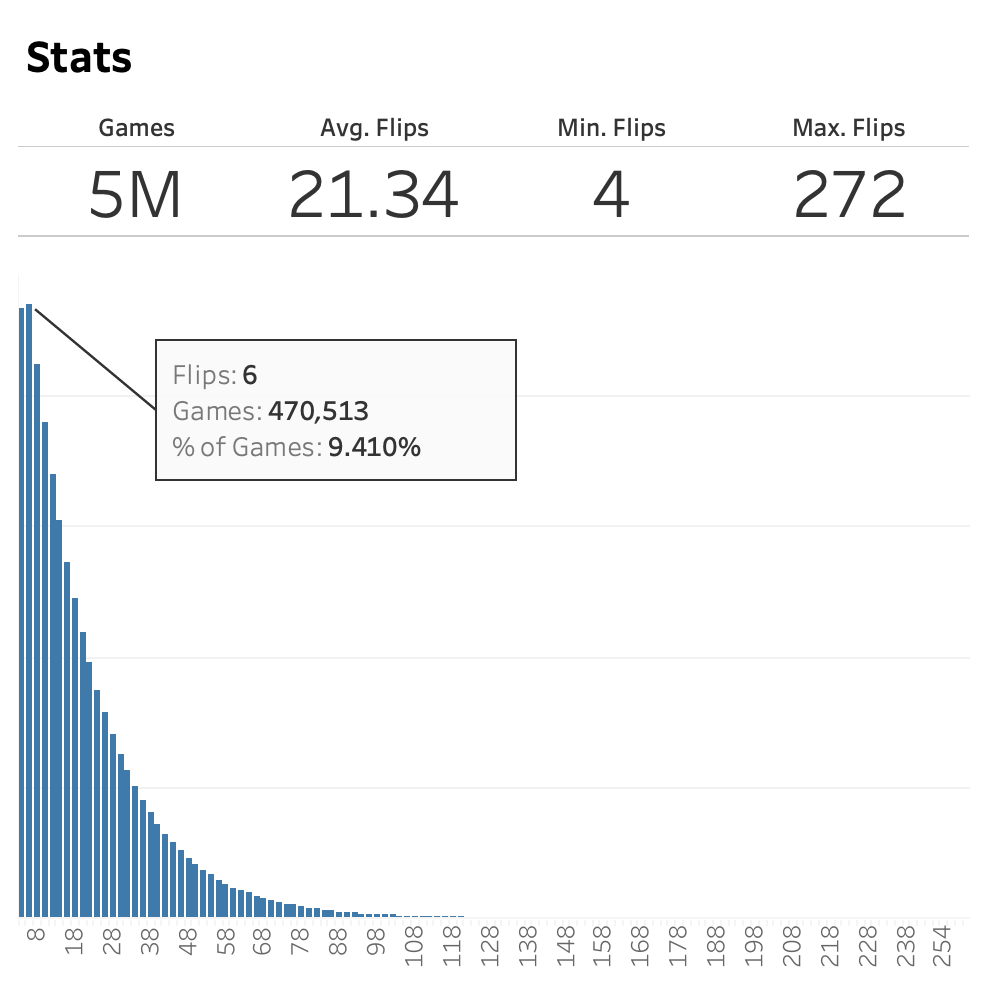
A number of solvers decided to simulate the pinball machine thousands or even millions of times, averaging the number of flips until all four lanes were lit. For example, 🎬 Angelos Tzelepis 🎬 ran the following Python script 5 million times:

lanes = [-1,-1,-1,-1]
flips = 0
while sum(lanes) < 4:
   flips += 1
   laneFlip = random.randint(1, 4)
   lanes[laneFlip-1] = lanes[laneFlip-1] * -1
print flips

The values of the four lanes were all initially set to -1, and randomly flipped one at a time to +1. As soon as the sum of the four lane values was +4, the required number of flips was recorded. Here was Angelos’s distribution of the number of flips across those 5 million simulations:

The distribution had a noticeably long tail, while the average was approximately 21.34.

Other solvers were able to confirm this result by setting up a system of equations. Suppose that when k lanes are already lit, the expected number of remaining flips until all four lanes were lit was f(k). Then our goal here was to solve for f(0). But we also knew that f(0) = 1 + f(1), since one flip guaranteed that one lane was lit, after which f(1) flips were required to light all four lanes. Similarly, you knew that f(1) = 1 + 1/4·f(0) + 3/4·f(2). In other words, flipping when one lane was lit had a 1-in-4 chance of flipping that lane’s light back off, but a 3-in-4 chance of flipping a second lane’s light on. A third equation was f(2) = 1 + 1/2·f(1) + 1/2·f(3), and a fourth equation was f(3) = 1 + 3/4·f(2) + 1/4·f(4). Of course, f(4) was zero, since that meant all four lanes were lit and no more flipping was needed. This meant f(3) = 1 + 3/4·f(2).

At this point, you had four equations with four unknowns. Solving these simultaneous equations gave you f(0) = 64/3, or 21 and 1/3 flips, very close to Angelos’s simulated result.

Solver Nicholas Strange got as far as noting the possible states of the pinball machine and the transitional probabilities between these states. From there, he asked ChatGPT-3.5 to write an Excel script for simulations. Apparently, it worked! Of course, when I dumped the original problem into ChatGPT-3.5, it set up the wrong system of equations and told me the answer was 6. Figures.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Izumihara Ryoma 🎻, from Toyooka, Japan. I received 35 timely submissions, of which 32 were correct—good for an impressive 91 percent solve rate.

For Extra Credit, instead of four lanes, your pinball game now had N lanes. Meanwhile, E(N) represented the average number of pinball flips it took until all N lanes were lit up.

Now, each time you increased the number of lanes by one, you found that it took you approximately twice as long to light up all the lanes. In other words, E(N+1) seemed to be about double E(N). 

But upon closer examination, you found that it wasn’t quite double. Moreover, there was a particular value of N where the ratio E(N+1)/E(N) was at a minimum. What was this value of N?

When there were four lanes, it wasn’t too painful to set up a system of equations and solve them. But with the more general case of N lanes, the algebra became increasingly prohibitive. Fortunately, there were still good techniques for solving this.

Evan Rittner placed the transition probabilities from the four-lane puzzle into what’s called a transition matrix, as shown below:

Each (row, column) in the transition matrix P gave the probability of transitioning from the state with the row’s number of lanes lit to the column’s number of lanes lit. With some linear algebra, Evan confirmed that the expected number of steps to reach the “absorbing state” with four lanes lit was 64/3. What’s more, adjusting this matrix to account for different numbers of lanes wasn’t too laborious. For example, if there had been five lanes instead of four, reading down the diagonal just above the matrix’s main diagonal you would have had 1, 0.8, 0.6, 0.4, and 0.2. From there, Evan was able to quickly compute E(N) for many values of N, which he used to observe where the minimum value of E(N+1)/E(N) occurred.

Solver Laurent Lessard explored why this ratio E(N+1)/E(N) approached 2 as N increased. Here was Laurent’s semilogarithmic plot of E(N+1)/E(N), which clearly showed the minimum occurred when N was 6:

A few solvers, including Laurent Lessard and Emilie Mitchell, went the extra mile by computing that E(7)/E(6) was 151/78, or approximately 1.936.

Last week’s winner, Izumihara Ryoma, went so far as to find an analogous continuous expression for E(N) using beta functions, and then determining the range of N for which E(N+1)/E(N) was less than both E(N)/E(N−1) and E(N+2)/E(N+1). According to Izumihara, this range was 5.84263 ≤ N ≤ 6.84263, for which N = 6 was the only integer solution.

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.