Can You Fail to Lose the Tennis Match?

You read that double negative right. What’s the greatest percentage of points you can lose in a tennis match, while still winning the match itself?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

From Chris Payne comes a tennis-themed puzzle that’s just in time for Wimbledon:

Consider a three-set tennis match. To win the match, you must win at least two of the three sets. To win a set, you must win a certain number of games. To win a game, you must win a certain number of points. For those who are unfamiliar with tennis, I’ll go into a little more detail.

A game is won by the first player who scores four points. However, the winner must “win by two.” So if both players have three points, they keep going until one player has two more points than their opponent, at which point the player with more points wins the game.

A set is won by the first player to win six games within the set. However, if both players have exactly five games each, then they play exactly two more games. If one player wins both of them, that player wins the set. If each player wins one of these games, so that they now have six games apiece, they proceed to a tiebreak.

A tiebreak is essentially a game that goes to seven points rather than four. The first to seven points wins, and players must win by two.

Keeping all this in mind, what is the greatest percentage of points (including tiebreak points) a player could lose in a three-set match, while still winning the match itself?

This Week’s Extra Credit

Assume a three-set tennis match features two players who are evenly matched, so that each player has a 50 percent chance of winning any given point. Also, points are independent, so the outcome of one point doesn’t affect the probability of who wins subsequent points.

How likely is it that one of the players loses a majority of the points in a match while winning the match itself? (Here, I mean a strict majority, i.e., more than 50 percent of the points.)

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a physics fact that I suppose I could have figured out at some point, but never actually thought about until I saw it on social media. I’ll restate the fact here:

It takes 2 hours to orbit at the surface of any object made of rock.

I mean—what?

Try working this out for yourself. For starters, you’ll want the centripetal force, mv²/R, to equal the gravitational force, GMm/R². And remember, for a circular orbit, the speed v is equal to 2𝜋R/T, where T is the orbital period.

Thanks to M scaling with R³ (you know, since we live in three dimensions), if you plug in an appropriate density for rock, you should discover a constant time of roughly 2 hours.

If you click the link above and read more in the thread, you’ll see how this is a decent approximation for the orbital periods near the surface of Earth, Mars, and the Moon. And it’s even cooler to see how this 2-hour period serves as a lower bound on the rotational periods for large asteroids. Cool stuff!

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Paige Kester 🎻 from Southlake, Texas. I received 29 timely submissions, of which 27 were correct—good for a 93 percent solve rate.

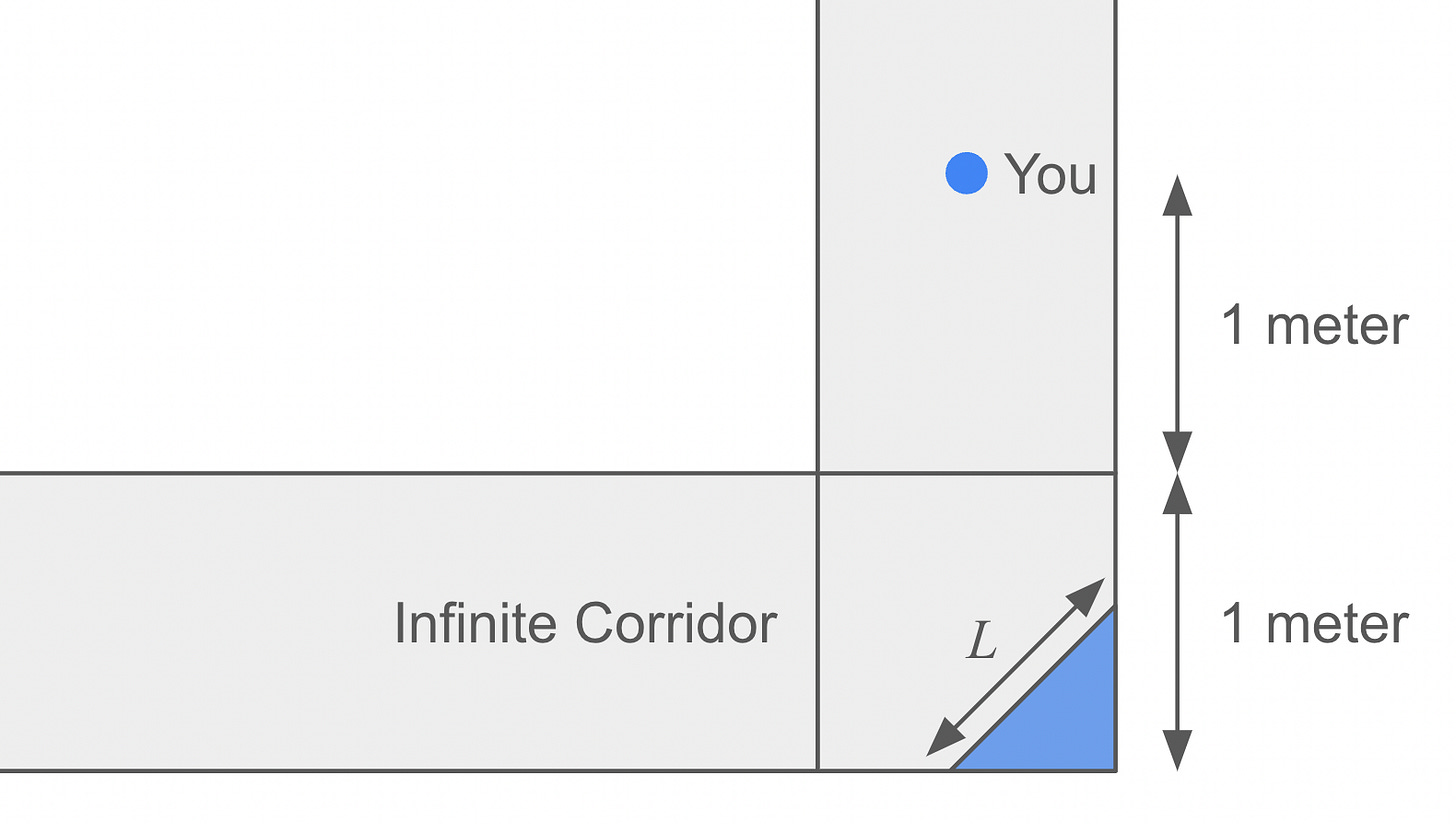
Last week, you were a senior member of the Fiddler Spy Agency. You had infiltrated an enemy base, as diagrammed below, and found yourself standing in the middle of a corridor that was 1 meter wide. You were 1 meter away from a square turn in the corridor, around which was a very long “infinite corridor” (so named because, well, it was very long).

Importantly, there was a flat mirror placed at a 45 degree angle in the far corner of the turn, as shown above. The mirror formed a 45-45-90 right triangle with that corner, such that its hypotenuse (i.e., the length of the mirror) was L.

For different values of L, you could “spy on” different sections of the infinite corridor. A given point in the infinite corridor could be spied upon if there was some location on the mirror that reflected light from that point to where you were standing.

What was the minimum value of L such that the mirror allowed you to spy on the entire infinite corridor? (Note that this was a puzzle in two, rather than three, dimensions.)

One of the keys to this puzzle was continuity. As your eyes swept across the mirror from one side to the other, you saw different parts of the hallway in one continuous stretch. So in order to see the entire infinite corridor, you just had to make sure you could see both extremes of the infinite corridor.

In other words, looking at the bottom-left corner of the mirror meant you had to see light coming from the bottom wall of the infinite corridor (or lower), while looking at the top-right corner of the mirror meant you had to see the very edge of the top wall, as shown below.

Again, as long as the extremes looked like this, then as the point you looked at in the mirror swept across the mirror, the ray of points coming off the mirror swept across the entire infinite corridor.

For the bottom-left corner of the mirror to reflect light below the bottom wall of the infinite corridor, that corner of the mirror had to be in the left half of the square where the hallways intersected. That meant each leg of the isosceles right triangle formed by the mirror had to be at least 0.5 meters, which in turn meant the mirror itself was at least 1/√2, or roughly 0.7071 meters. So as long as L was at least 0.7071 meters in length, you’d be able to see the entire bottom wall of the infinite corridor—but not necessarily the top wall.

The condition on the top-right corner was a little tricker to figure out. Solver 🎬 Mark Pilloff 🎬 sketched the following diagram:

Now, mirrors reflect light in a very specific way: Their angle of incidence equals their angle of reflection. Here, because the mirror was situated with the walls at a 45-degree angle, that meant the two blue angles with a vertex of H’ (the top right corner of the mirror) were congruent. And because those angles were congruent, that meant the two blue right triangles were similar.

If each leg of the mirror’s isosceles right triangle had length x, then the bottom blue right triangle had legs of length 1−x and 1. Meanwhile, the top blue right triangle had legs of length 0.5 and 2−x. Because these two triangles were similar, the ratios of their side lengths were equal. In other words, (1−x)/1 = 0.5/(2−x), which could be rearranged into the quadratic equation 2x² − 6x + 3 = 0.

Applying the quadratic formula—and keeping the smaller solution, which was less than 1— revealed that x = (3−√3)/2. The mirror’s length was √2 times greater, which meant L = (3−√3)/√2, or approximately 0.897 meters. For the record, I was totally fine with solutions with irrational denominators like this. In the words of solver Eric Widdison, “Yes, I know that my high school math teachers would like me to rationalize the denominator, but calculators make that exercise unnecessary, and this is the more elegant form.”

If you’re still not convinced that the entire infinite corridor was visible with a mirror of this size, then solver 🎬 Rohan Lewis 🎬 had just the animation for you! Here’s Rohan’s animation showing how your line of sight across the length of the mirror scanned every point in the infinite corridor:

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Jason Weisman 🎻 from Wilton, Connecticut. I received 11 timely submissions, of which 9 were correct—good for an 82 percent solve rate. This was a tough one!

For Extra Credit, the flat mirror was no longer constrained to be at a 45 degree angle with the corner. That said, it still had to be flush against the corner so that it formed a right triangle, as illustrated below:

Once again, what was the minimum length of the hypotenuse L such that the mirror allowed you to spy on the entire infinite corridor?