Can You Escape the Infinite Loop?

That's right. The Fiddler is here!

Welcome to the inaugural edition of Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of Zach Wissner-Gross and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Beyond these, I also hope to share occasional writings about the broader mathematical and puzzle communities.

Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many will include “extra credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

This week, it’s all about Möbius strips!

Suppose I start with a strip of paper that’s 10 inches long and 1 inch wide. I twist it once and attach the two 1-inch edges together, forming a Möbius strip. Finally, I draw a dot somewhere in the center of the strip—that is, the dot is half an inch away from both edges.

Naturally, the distance between any two points on my strip is the shortest path between them, as the ant crawls. By that, I mean that such paths can go over an edge to the other “side” of the strip (“side” in quotes because it’s all really the same side, after all), just as an ant would crawl around the edge of the paper.

There is a point (or points) on the strip that is the farthest distance from my dot. What is this distance?

This Week’s Extra Credit

Instead of a strip of paper, consider a three-dimensional prism whose bases are regular N-gons. I twist it and stretch it into a loop, before finally connecting the two bases. Suppose that my twist is by a random angle, such that the two bases are aligned when they are connected. I’m interested in how many distinct faces there are in the resulting “Möbius prism.”

For example, let’s say the original figure is a square prism (i.e., N = 4). There are four kinds twists I can apply, all equally likely:

• A one-quarter twist, which results in one distinct face

• A two-quarter (or one-half) twist, which results in two distinct faces

• A three-quarter twist, which results in one distinct face

• A four-quarter (or whole) twist, which results in four distinct faces

A randomly twisted square prism will have, on average, (1+2+1+4)/4, or two distinct faces.

Among all whole number values of N less than or equal to 1,000, for which value of N will a randomly twisted regular N-gon prism have the most distinct faces, on average?

Making the Rounds

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing a puzzle I saw via Twitter on June 24, 2023:

At first glance, the question itself seems to violate the fundamental theorem of algebra. But upon deeper inspection, you’ll see that’s not the case. It’s up to you to figure out how.

Last Week’s Fiddler

As this is the inaugural column, there was no Fiddler last week. But rumor has it there was a final Riddler column whose puzzle has gone unanswered. Let’s take a look at that one, shall we?

Congratulations to the (randomly selected) winner from last week: 🎻 Srihari Narayanan 🎻, from Hayward, California. For this final Riddler, I received 20 timely submissions (well under the usual number, perhaps due to folks feeling like this was the end), of which 17 were correct. An 85 percent solve rate—way to go, team!

In that final Riddler, there was a 184-gon (i.e., a polygon with 184 sides) inscribed in a circle. The polygon was not regular, meaning its sides and angles could have different measures. The points around the polygon were labeled ABCDEFGH …, and you measured alternating angles (i.e., angles ABC, CDE, EFG, etc.). In total, you measured 92 angles. If the first 89 of them each measured 178 degrees, what was the sum of the final three angles?

First off, the context of this puzzle involved a laser bouncing off a circular mirror. Since the angles of incidence and reflection are equal for light bouncing off of mirrors, the irregularity of this 184-gon didn’t make physical sense. Thanks to Bradon Zhang and Glenn Horton-Smith for pointing this out!

Putting the (incorrect) physics aside, let’s get back to the math. Many readers were already familiar with the formula for calculating the sum of the internal angles—in degrees—of a polygon with N sides: (N−2)·180. That meant the sum of all the angles in the 184-gon was 182·180, or 36,760 degrees. But you needed more information than that.

The key piece of information here was that the 184-gon was cyclic, meaning there existed a circle such that every vertex was on the circle. The angles of cyclic polygons exhibit a number of special relationships, due to the fact that an angle inscribed in a circle always measures half the arc it subtends.

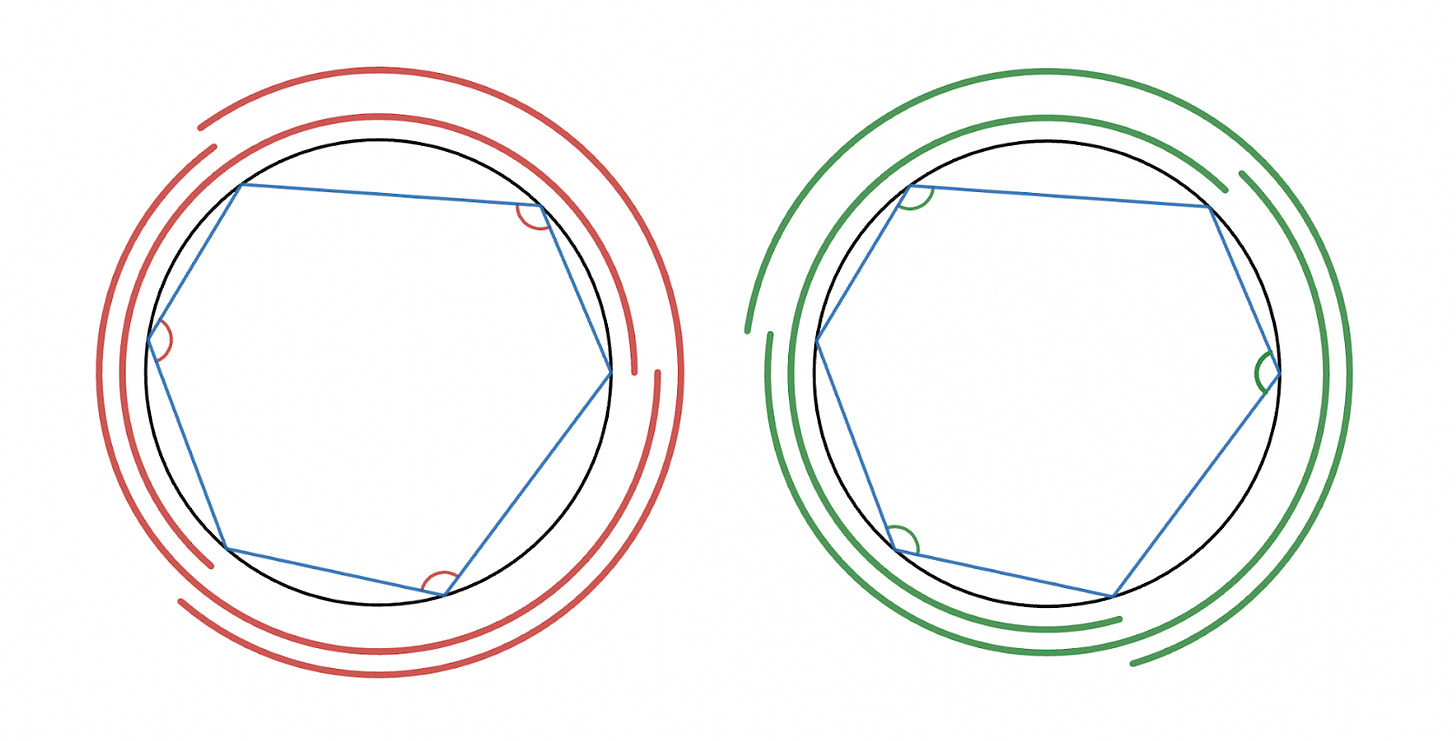
Instead of jumping straight to a 184-gon, let’s first look at a polygon with fewer vertices, like a hexagon. The six angles in a cyclic hexagon can be split into two trios of alternating angles. These trios are highlighted in the image below, while the subtended arcs are illustrated outside the circles.

As we said earlier, each inscribed angle measures half its subtended arc, which means the sum of each angular trio is half the sum of the three arcs. What’s important here is that the sum of the arcs is the same for both sets of angles—in both cases, the arcs combine to wrap around the circle twice, for a total measure of 720 degrees. And because the sums of the arcs are the same, the sums of the angular trios must also be the same.

Similar reasoning could also be applied to the 184-gon, or any cyclic polygon with an even number of vertices. The angles in such an N-gon can be split up into two sets of alternating angles, both of which have the same combined sum of (N−2)·90.

Returning to our original problem, that meant the 92 angles had a combined measure of (184−2)·90, or 16,380 degrees. You already knew that 89 of those angles each measured 178 degrees, for a total of 15,842 degrees. That meant the sum of the last three angles was 16,380−15,842, or 538 degrees.

Of course that was the answer to the final Riddler at FiveThirtyEight.

The Final Battle for Riddler Nation

Once upon a time, I conducted a Final Battle for Riddler Nation over at FiveThirtyEight. I even summarized the results, including the top 10 finishers, in my final column. But a number of folks have reached out to me personally, asking for the complete standings and list of strategies. I am happy to oblige: Here are the complete results!

Note that should you find any errors in how I conducted the round robin madness, please message me discreetly and expect only a facepalm emoji as my reply.

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.