Can You Bounce a Ball Like an AI?

LLMs are being benchmarked by simulating a ball bouncing inside a polygon. Can you find cases where the ball keeps making contact at a single point?

Welcome to Fiddler on the Proof! The Fiddler is the spiritual successor to FiveThirtyEight’s The Riddler column, which ran for eight years under the stewardship of myself and Ollie Roeder.

Each week, I present mathematical puzzles intended to both challenge and delight you. Puzzles come out Friday mornings (8 a.m. Eastern time). Most can be solved with careful thought, pencil and paper, and the aid of a calculator. Many include “Extra Credit,” where the analysis gets particularly hairy or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after that puzzle was released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

A recent trend for benchmarking AI performance is to have LLMs write code simulating a ball bouncing around a rotating polygon, which involves kinematics and collision detection. It turns out it’s fairly tricky for some LLMs to implement this, and has led to humorous failed attempts.

I won’t be asking you to code such a simulation this week, although you’re welcome to do so!

Instead, suppose you have a unit square that’s rotating about its center at a constant (nonzero) angular speed, and there’s a moving ball inside. The ball has a constant (nonzero) linear speed, and there’s no friction or gravity. When the ball hits an edge of the square, it simply reflects as though the square is momentarily stationary during the briefest of moments they’re in contact. Also, the ball is not allowed to hit a corner of the square—it would get jammed in that corner, a situation we prefer to avoid.

Suppose the ball travels on a periodic (i.e., repeating) path, and that it only ever makes contact with a single point on the unit square. What is the shortest distance the ball could travel in one complete loop of this path?

This Week’s Extra Credit

Again, you have a rotating unit square and bouncing ball inside.

By now, you’ve hopefully found the shortest repeating path for which the ball makes contact with a single point on the square. Let’s call this path length L₁.

The next shortest repeating path for which the ball makes contact with a single point on the square has length L₂. To be clear, L₂ > L₁.

What is the length L₂?

Making the ⌊Rounds⌉

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing the February monthly challenges from Amplify (my employer by day).

Keeping with the AI theme, one of the challenges (authored by yours truly) allows you to train your own neural network to classify your sketches. You’re welcome to try the complete activity, which gets into some (but certainly not all) of the math behind neural networks, or you can just train your own network.

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Standings

I’m tracking submissions from paid subscribers and compiling a leaderboard, which I’ll reset every quarter. All timely correct solutions to Fiddlers and Extra Credits are worth 1 point each. At the end of each quarter, I’ll 👑 crown 👑 the finest of Fiddlers. (If you think you see a mistake in the standings, kindly let me know.)

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Thomas Stone 🎻 from San Francisco, California. I received 74 timely submissions, of which 74 were correct—good for a perfect 100 percent solve rate (my favorite)!

Last week, you were sketching a graph for a math exam. Your graph had to be a function, which meant it had to pass the vertical line test: No vertical line could intersect your graph more than once.

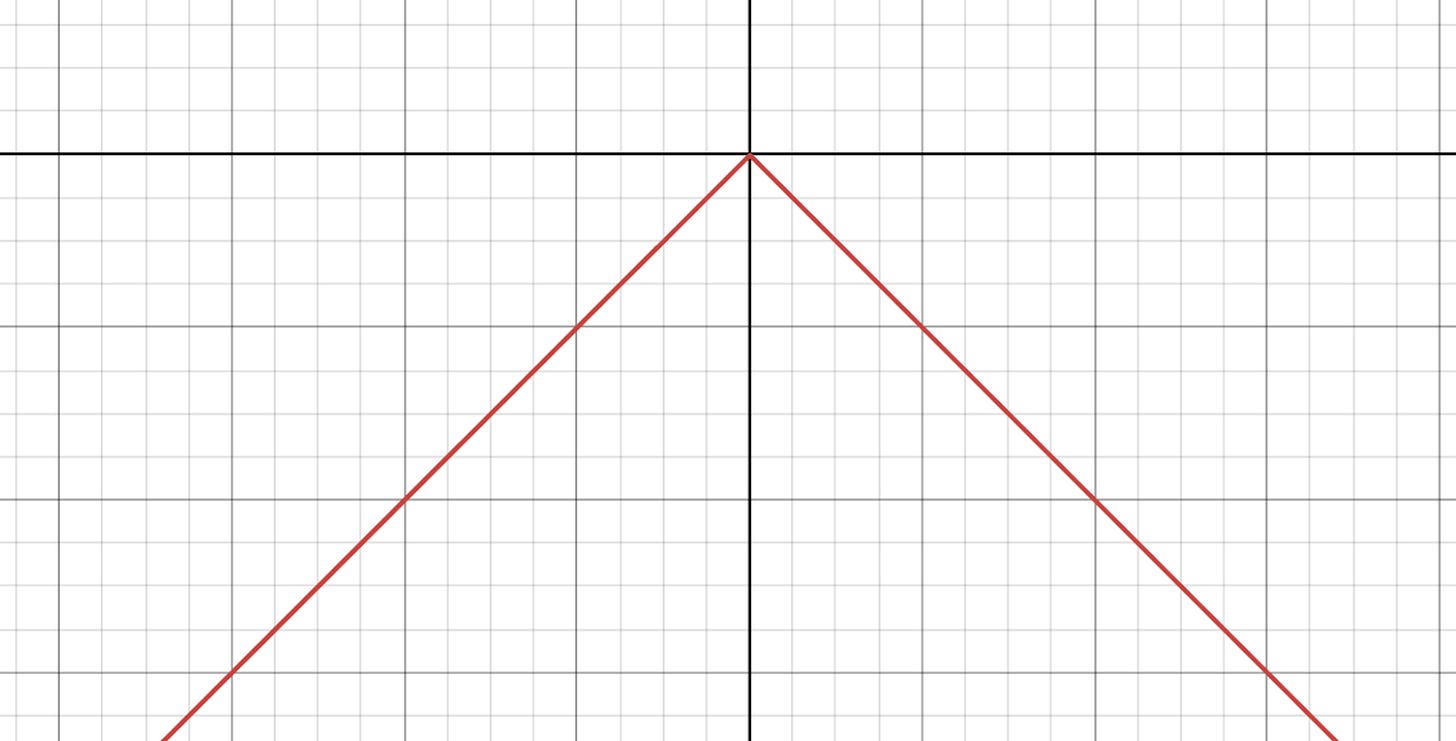
You decided you were going to graph the absolute value function, y = |x|, and ace the test.

There was just one problem. You were dealing with a bout of dizziness, and couldn’t quite make out the x- and y-axes on the exam in front of you. As a result, your function was rotated about the origin by a random angle that was uniformly chosen between 0 and 360 degrees.

What was the probability that the resulting graph you produced was in fact a function (i.e., y was a function of x)?

Of course, when you didn’t rotate the graph at all, it was a function. But if you rotated the graph slightly (20 degrees clockwise around the origin, let’s say), it was still a function:

Once you rotated the graph at least 45 degrees, it failed the vertical line test, and was no longer a function. For example, here was a 60-degree clockwise rotation, along with a vertical line (in blue) that passed through the graph at two points:

If you kept on rotating, eventually the graph flipped over, resembling the function y = -|x|, which was indeed a function:

By the time you hit 225 degrees in the clockwise direction, the graph failed the vertical line test again. But it became a function once more when you hit 315 degrees.

Putting this all together, you had 90 degrees of wiggle room (45 degrees clockwise and 45 degrees counterclockwise) when the function opened upward (y = |x|), and another 90 degrees of wiggle room when the function opened downward (y = -|x|). And so, out of the 360 degrees you could have randomly rotated the graph, 180 degrees resulted in a function. The answer was therefore 180/360, or 1/2.

For this problem, it was quite reasonable to assume that any rotation by a real-valued number of degrees was allowed. Some readers assumed, however, that only rotations by whole number degree amounts were allowed. In this case, the answer would have been 178/360 (slightly less than 1/2), since you had to exclude edge cases where part of the function was vertical. While this wasn’t the intent of the puzzle, I still awarded this answer with credit.

By the way, an alternate way to think about the problem was to have the graph fixed, and to instead have the y-axis rotated randomly. As long as the y-axis (or the negative y-axis) was contained inside the “funnel” of the graph, the graph would pass the vertical line test.

Because the absolute value function contains a 90 degree angle at its vertex, the probability the y-axis lay within its funnel was 90/360, or 1/4. Meanwhile, the probability that the negative y-axis lay within the funnel was also 90/360, or 1/4. Therefore, the probability that one of them lay within the funnel was 1/4 + 1/4, or 1/2—exactly the answer we found by randomly rotating the graph (rather than the coordinate system).

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 Josh Silverman 🎻 from Glen Head, New York. I received 28 timely submissions, of which 12 were correct—good for a 43 percent solve rate.

In a more advanced course, you were asked to draw a 3D sketch of the function z = |x| + |y|. As you were about to do this, you were struck by another bout of dizziness, and your resulting graph was randomly rotated in 3D space.

More specifically, your graph had the correct origin. But the true z-axis was equally likely to point from the origin to any point on the surface of the unit sphere. (Meanwhile, the x-axis was equally likely to point in any direction perpendicular to the z-axis. From there, the y-axis was uniquely determined.)

What was the probability that the resulting graph you produced was in fact a function (i.e., z was a function of x and y)?