Bingo!

On average, how long will it take you to get three (or five) in a row?

Welcome to Fiddler on the Proof, the spiritual successor to FiveThirtyEight’s The Riddler column.

Every Friday morning, I present mathematical puzzles intended to challenge and delight you. Most can be solved with careful thought, pencil and paper, and the aid of a calculator. The “Extra Credit” is where the analysis typically gets hairy, or where you might turn to a computer for assistance.

I’ll also give a shoutout to 🎻 one lucky winner 🎻 of the previous week’s puzzle, chosen randomly from among those who submit their solution before 11:59 p.m. the Monday after puzzles are released. I’ll do my best to read through all the submissions and give additional shoutouts to creative approaches or awesome visualizations, the latter of which could receive 🎬 Best Picture Awards 🎬.

This Week’s Fiddler

A game of bingo typically consists of a 5-by-5 grid with 25 total squares. Each square (except for the center square) contains a number. When a square’s number is called, you place a marker on that square. The goal is to get “bingo,” which is five squares in a row, either across, down, or along one of the two long diagonals. The center square, which doesn’t have a number, is labeled “Free,” and begins with a marker on it before any numbers are called. Here’s an example of a winning 5-by-5 grid in which 10 squares (other than the “Free” square) have been marked:

Consider a smaller version of the game with a 3-by-3 grid: a “Free” square surrounded by eight other squares with numbers. Suppose each of these eight squares is equally likely to be called, and without replacement (i.e., once a number is called, it doesn’t get called again).

On average, how many markers must you place until you get “bingo” in this 3-by-3 grid? (The “Free” square doesn’t count as one of the markers—it’s “free”.)

This Week’s Extra Credit

Instead of a 3-by-3 grid, let’s return to the original 5-by-5 grid.

On average, how many markers must you place until you get “bingo”? (As before, the “Free” square doesn’t count as one of the markers—it’s “free”.)

Making the ⌊Rounds⌉

There’s so much more puzzling goodness out there, I’d be remiss if I didn’t share some of it here. This week, I’m sharing that the National Museum of Mathematics (MoMath) will be hosting an in-person SET tournament on Sunday, February 1. If you’re in the New York area, you should go!

And if you’ve never played SET, I highly recommend it. It’s a game that’s rich with mathematical intrigue and puzzles.

Want to Submit a Puzzle Idea?

Then do it! Your puzzle could be the highlight of everyone’s weekend. If you have a puzzle idea, shoot me an email. I love it when ideas also come with solutions, but that’s not a requirement.

Standings

I’m tracking submissions from paid subscribers and compiling a leaderboard, which I’ll reset every quarter. All correct solutions to Fiddlers and Extra Credits are worth 1 point each. Solutions should be sent prior to 11:59 p.m. the Monday after puzzles are released. At the end of each quarter, I’ll 👑 crown 👑 the finest of Fiddlers. If you think you see a mistake in the standings, kindly let me know.

Last Week’s Fiddler

Congratulations to the (randomly selected) winner from last week: 🎻 Ryan 🎻 from Raleigh, North Carolina. I received 65 timely submissions, of which 39 were correct—good for a 60 percent solve rate.

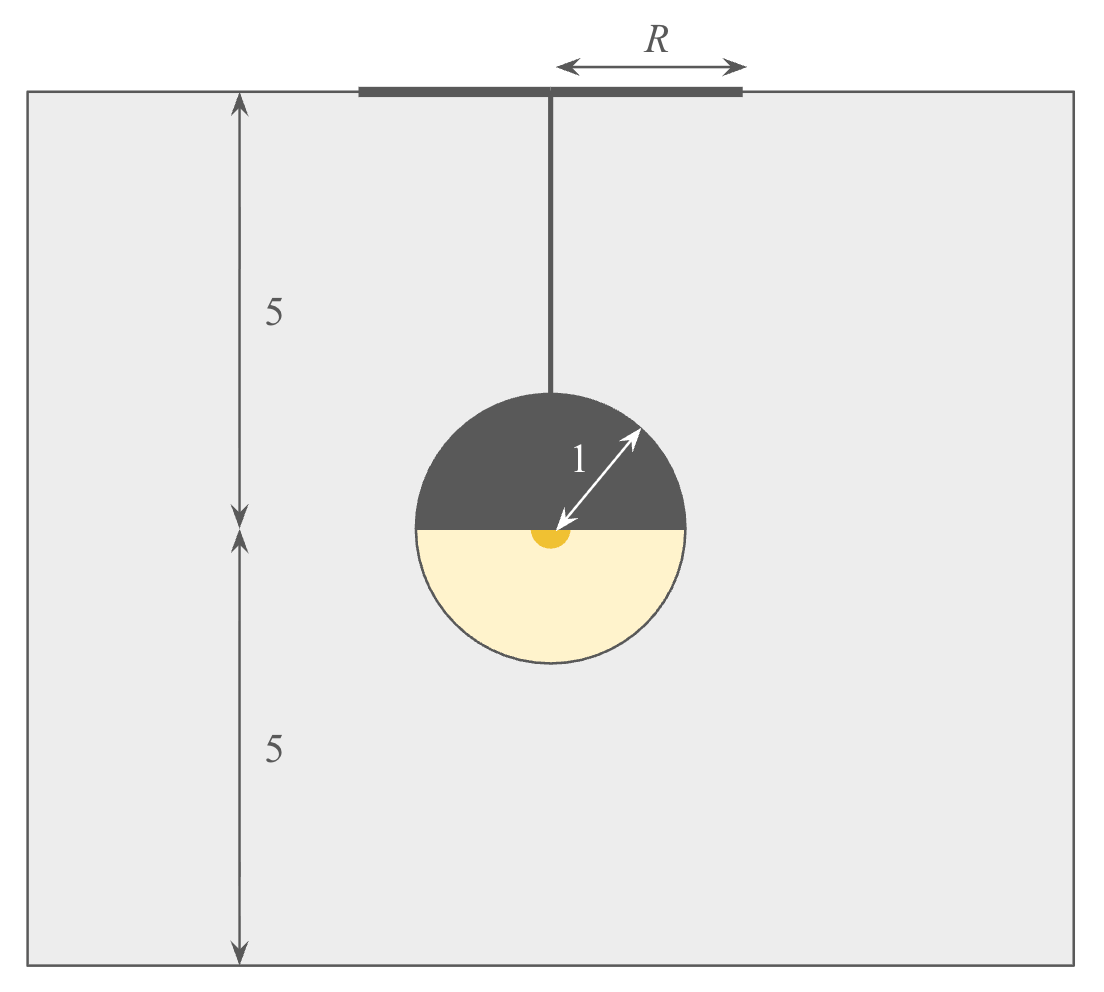
Last week, while dining at a restaurant, I noticed a lamp descending from the ceiling, as shown in the diagram below. The lamp consisted of a point light source at the center of a spherical bulb with a radius of 1 foot. The top half of the sphere was opaque, while the bottom half was semi-transparent, allowing light out (and thus illuminating my table) but not back in. The light source itself was halfway up to the ceiling—5 feet off the ground and 5 feet from the ceiling. The ground reflected light.

Above the light, on the ceiling, I saw a circular shadow. What was the radius R of this shadow?

To figure this out, you had to search for the closest a ray of light could get to the point on the ceiling directly above the light source. This minimum distance was the radius of the resulting circular shadow. Of course, light couldn’t hit the central point itself, since it was blocked by the spherical lamp itself. Instead, the ray in question traveled downward from the source, reflected off the floor, and then went up to the ceiling while narrowly avoiding the spherical lamp itself.

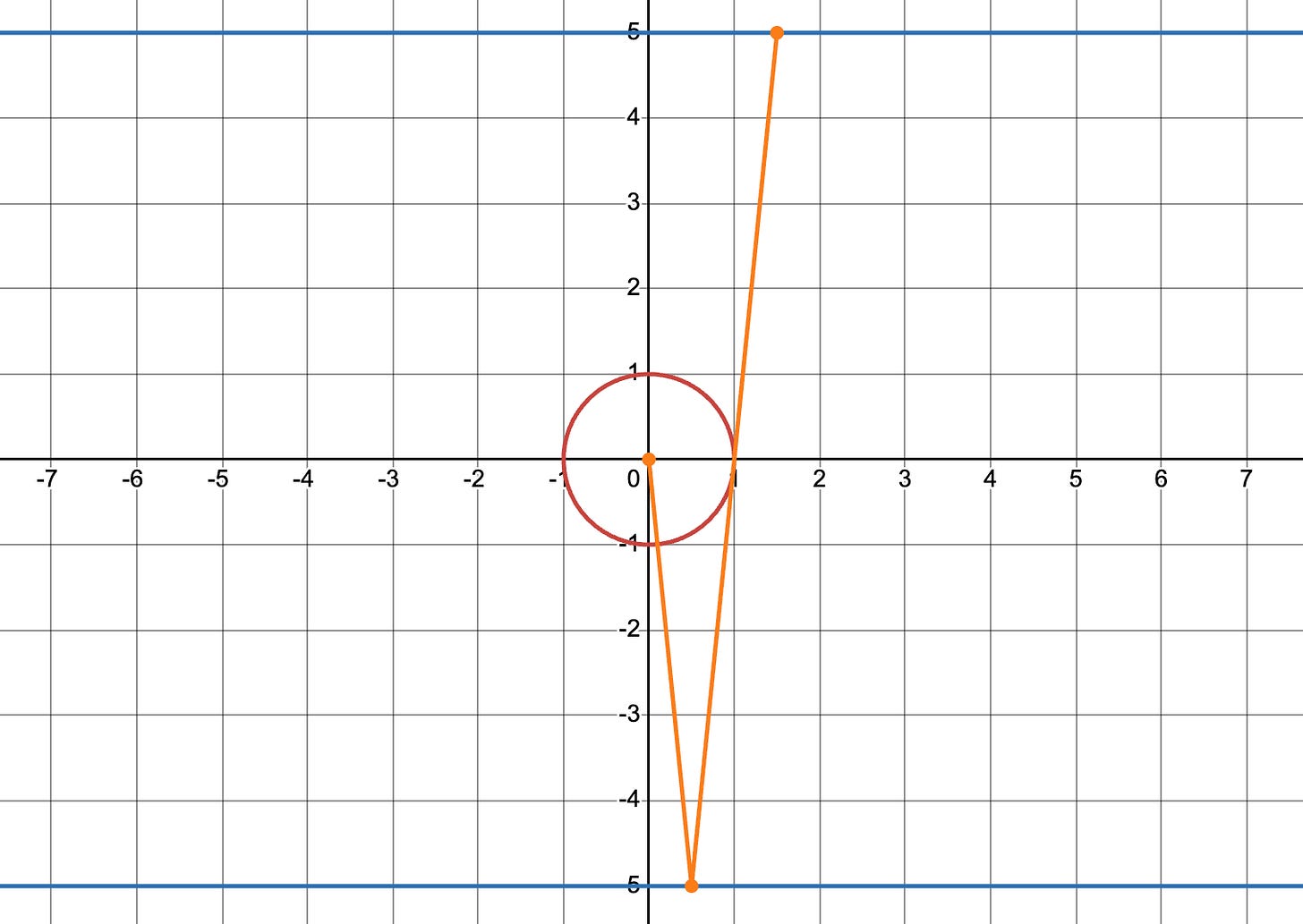
Quite a few readers used a diagram like the one below to illustrate this:

In this diagram, the light source was at the origin, while the light narrowly missed the circular outline of the bulb at the point (1, 0). This in turn meant that the light hit the floor at (0.5, -5) and the ceiling at (1.5, 5). Thus, the radius of the shadow was 1.5 feet. This answer was rather popular, accounting for 26 percent of reader submissions.

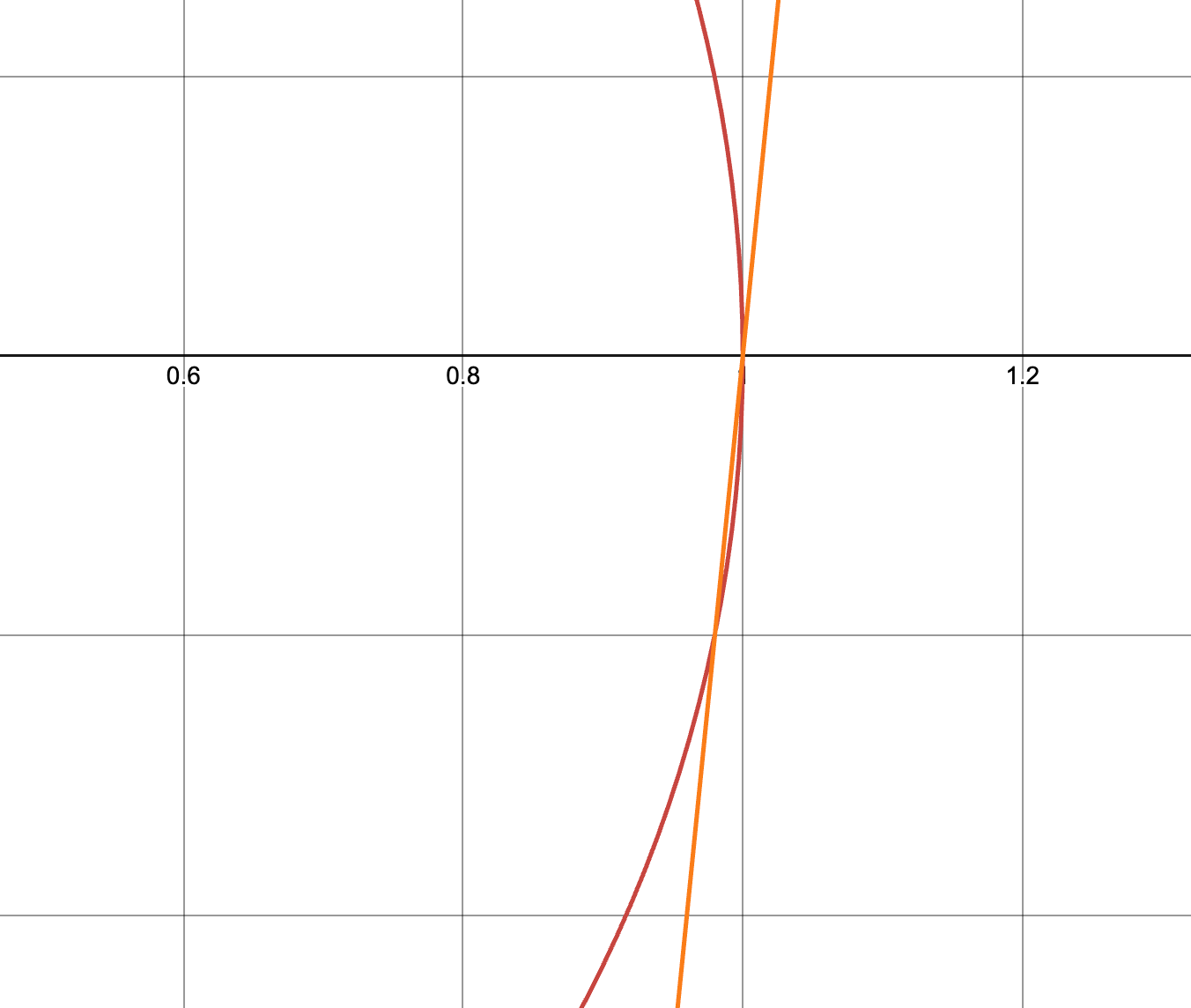
There was just one problem: This path actually passed through the spherical bulb, a fact which became apparent if you zoomed in around (1, 0). In the diagram below, the bulb’s circular profile is shown in red, while the light’s path is in orange. Sure enough, they cross over each other.

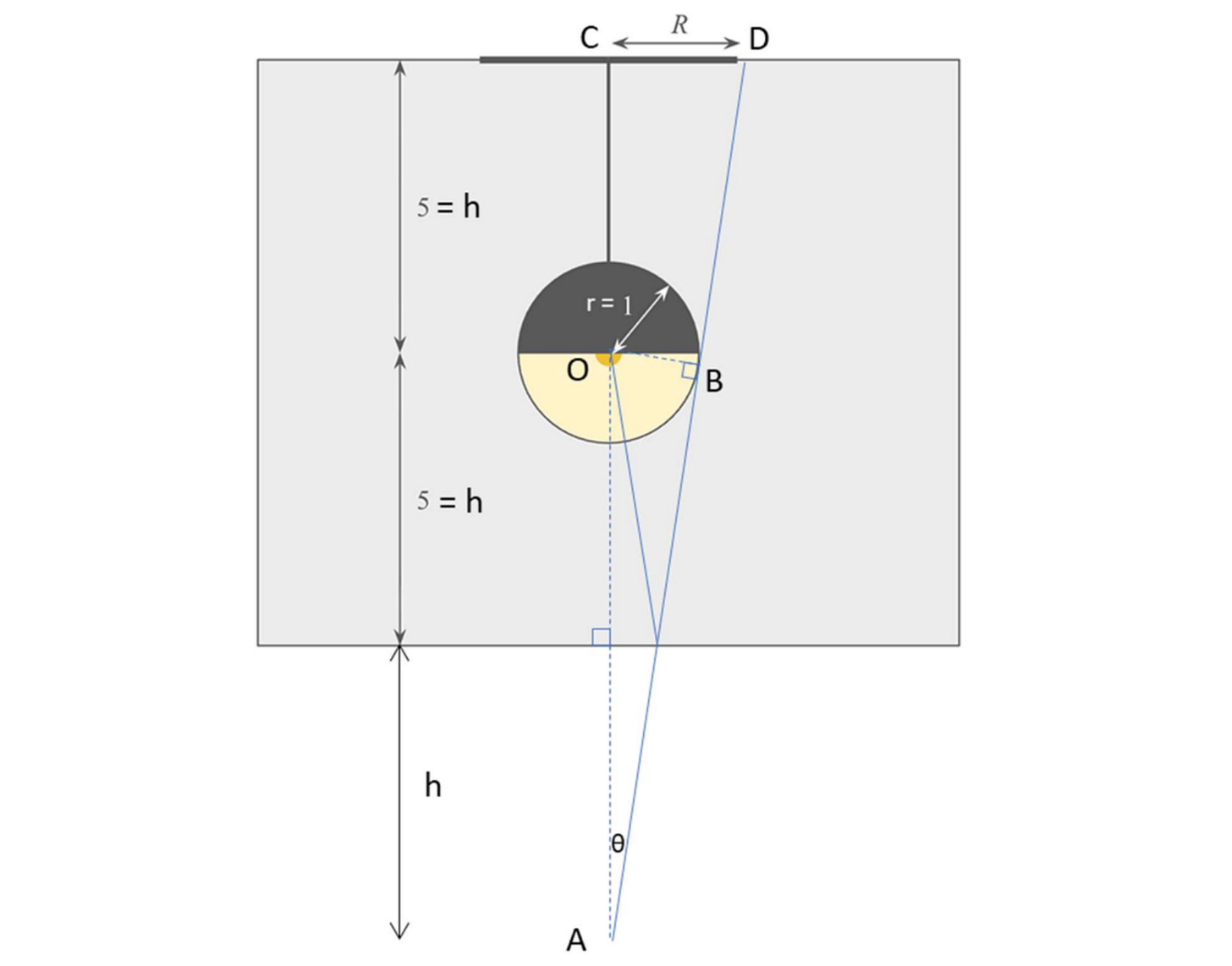
Instead of touching the circle at (1, 0), you wanted to find the ray of light that was tangent to the circle en route to the ceiling. Solver Laurent Mandorla adapted my original diagram (which admittedly wasn’t to scale) to highlight the tangency between the light and the circle:

Note that B, the point of tangency, was not directly to the right of the light source, but also slightly lower. Meanwhile, O was the light source and A was this point reflected through the floor, 10 feet down from O. Finally, C was the point on the ceiling directly above O and D was where the light hit the ceiling.

Laurent defined 𝜽 as the angle from vertical for the original downward ray that ultimately slipped past the bulb. From the right triangle ABO, we have sin(𝜽) = 1/10. Meanwhile, from triangle ACD, we have tan(𝜽) = R/15. Using these two equations (with their two unknowns), you could solve for R.

First, you could use the trigonometric identity sin²(𝜽) + cos²(𝜽) = 1 to find that cos(𝜽) = 3·√(11)/10. Then, with the identity tan(𝜽) = sin(𝜽)/cos(𝜽), you had R/15 = (1/10)/[3·√(11)/10] = 1/[3·√(11)]. Solving for R gave you 5/√(11), or approximately 1.50756 feet. This was just a smidge greater than the incorrect answer of 1.5 feet. Therefore, I accepted any answer that was exact or rounded off to 1.507 or 1.508, but I did not accept answers of 1.5.

Last Week’s Extra Credit

Congratulations to the (randomly selected) winner from last week: 🎻 John O’Donoghue 🎻 from Eugene, Oregon. I received 47 timely submissions, of which 30 were correct—good for a 64 percent solve rate.

Now suppose the lamp had a radius r and was suspended a height h off the ground in a room with height 2h. Again, the radius of the shadow on the ceiling was R.

For whatever reason, the restaurant’s architect insisted that she wanted r, h, and R, as measured in feet, to all be whole numbers. What was the smallest value of R for which this was possible?